วิธีการดำเนินการ spline regression ใน r (พร้อมตัวอย่าง)

การถดถอยแบบเส้นโค้ง เป็นการถดถอยประเภทหนึ่งที่ใช้เมื่อมีจุดหรือ “ปม” ซึ่งรูปแบบในข้อมูลเปลี่ยนแปลงอย่างกะทันหัน และ การถดถอยเชิงเส้น และ การถดถอยพหุนาม ไม่ยืดหยุ่นเพียงพอที่จะปรับให้พอดีกับข้อมูล

ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีการดำเนินการถดถอยแบบเส้นโค้งใน R

ขั้นตอนที่ 1: สร้างข้อมูล

ขั้นแรก เรามาสร้างชุดข้อมูลใน R ที่มีตัวแปรสองตัว และสร้างแผนภูมิกระจายเพื่อแสดงภาพความสัมพันธ์ระหว่างตัวแปร:

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

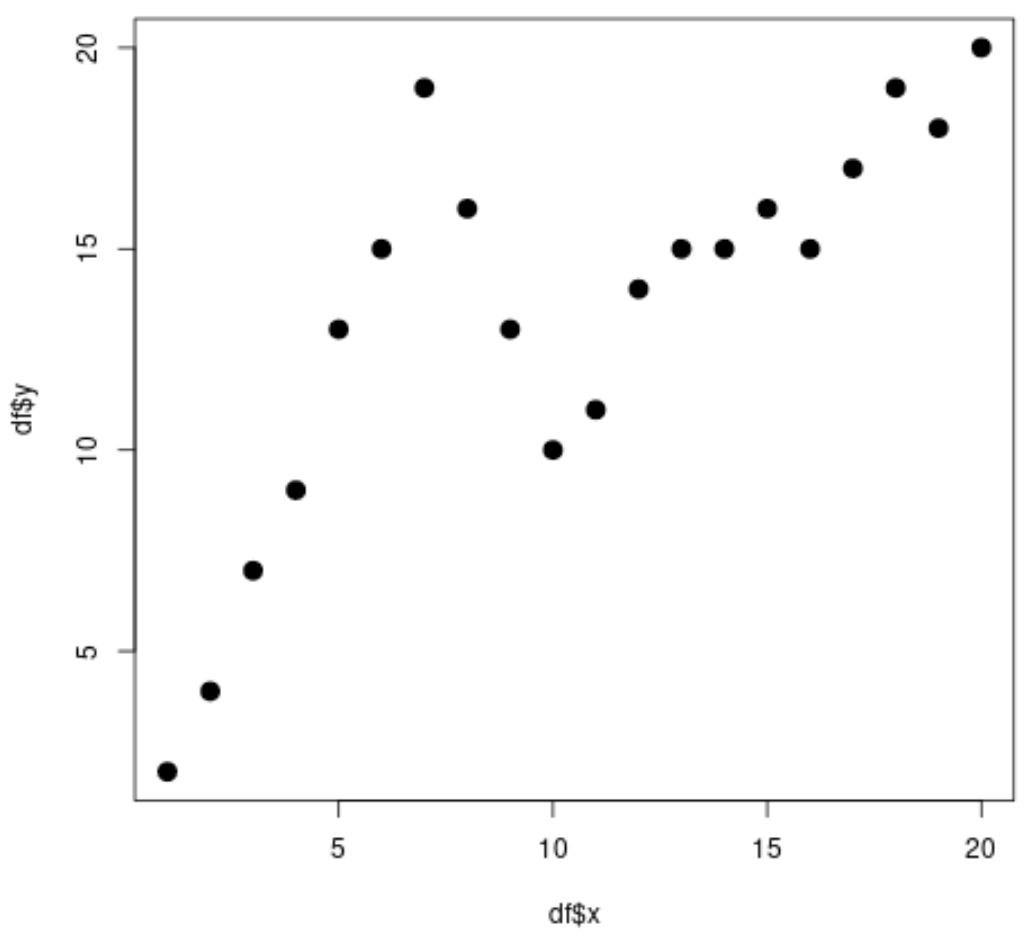
แน่นอนว่าความสัมพันธ์ระหว่าง x และ y นั้นไม่เป็นเชิงเส้น และดูเหมือนว่าจะมีสองจุดหรือ “โหนด” ซึ่งรูปแบบในข้อมูลเปลี่ยนแปลงอย่างกะทันหันที่ x=7 และ x=10

ขั้นตอนที่ 2: ติดตั้งโมเดลการถดถอยเชิงเส้นอย่างง่าย

จากนั้น ลองใช้ ฟังก์ชัน lm() เพื่อปรับโมเดลการถดถอยเชิงเส้นอย่างง่ายให้เข้ากับชุดข้อมูลนี้และลงจุดให้พอดีกับเส้นการถดถอยบน Scatterplot:

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

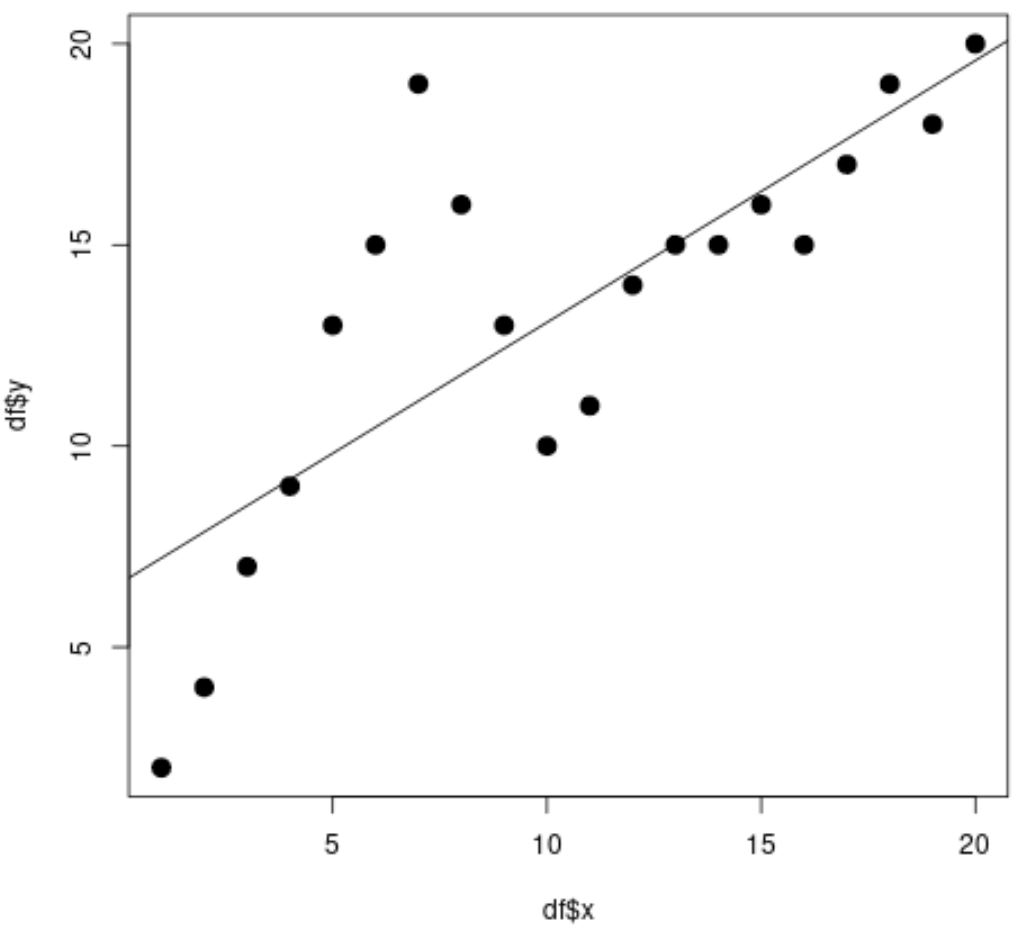
จากแผนภาพกระจาย เราจะเห็นว่าเส้นการถดถอยเชิงเส้นอย่างง่ายไม่พอดีกับข้อมูล

จากผลลัพธ์ของโมเดล เรายังเห็นได้ว่า ค่า R-squared ที่ปรับแล้ว คือ 0.5903

เราจะเปรียบเทียบสิ่งนี้กับค่า R-squared ที่ปรับแล้วของโมเดลเส้นโค้ง

ขั้นตอนที่ 3: ติดตั้งโมเดลการถดถอยแบบเส้นโค้ง

ต่อไป ลองใช้ฟังก์ชัน bs() จากแพ็คเกจ Splines เพื่อให้พอดีกับโมเดลการถดถอยแบบ Spline ด้วยสองโหนด จากนั้นจึงลงจุดโมเดลที่พอดีบน Scatterplot:

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

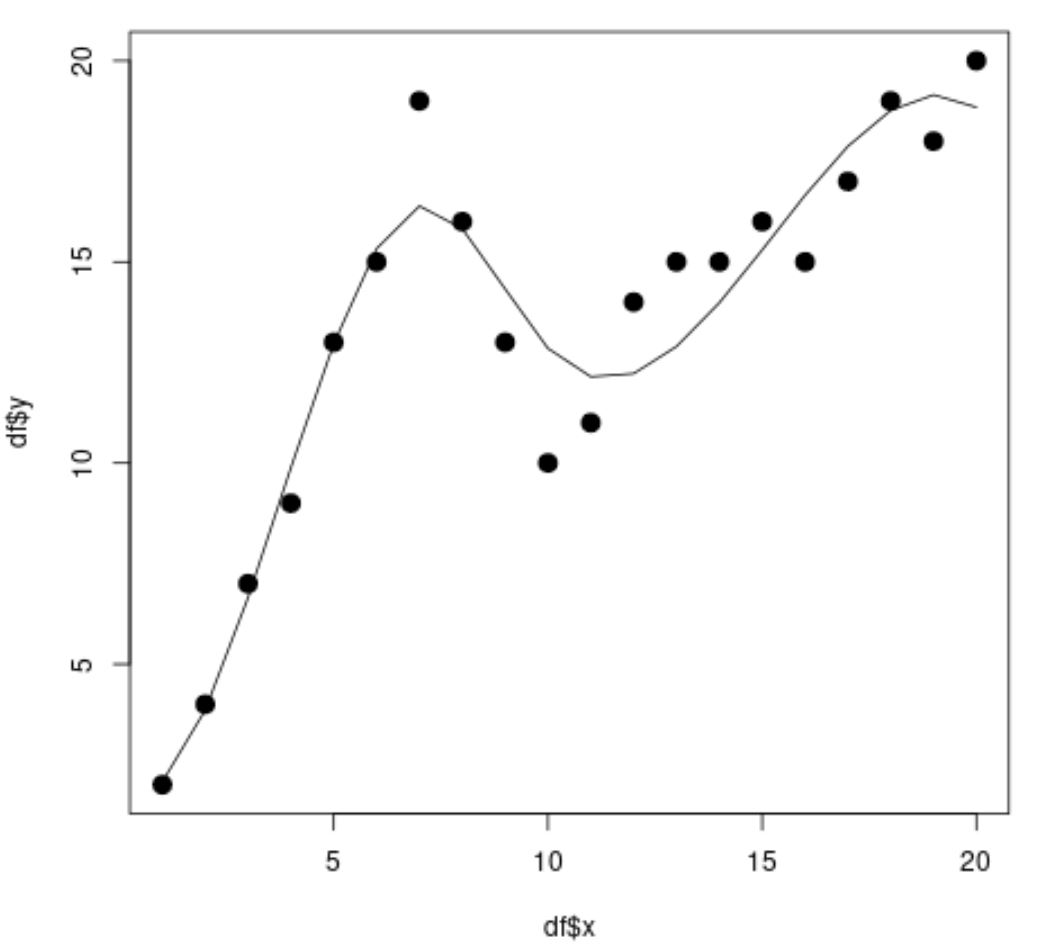
จากแผนภาพกระจาย เราจะเห็นว่าแบบจำลองการถดถอยแบบเส้นโค้งสามารถใส่ข้อมูลได้ค่อนข้างดี

จากผลลัพธ์ของโมเดล เรายังเห็นได้ว่าค่า R-squared ที่ปรับแล้วคือ 0.8987

ค่า R-squared ที่ปรับแล้วสำหรับโมเดลนี้สูงกว่าโมเดลการถดถอยเชิงเส้นแบบธรรมดาอย่างมาก ซึ่งบอกเราว่าโมเดลการถดถอยแบบเส้นโค้งสามารถใส่ข้อมูลได้ดีขึ้น

โปรดทราบว่าสำหรับตัวอย่างนี้ เราได้เลือกว่าโหนดอยู่ที่ x=7 และ x=10

ในทางปฏิบัติ คุณจะต้องเลือกตำแหน่งของโหนดด้วยตนเองโดยพิจารณาจากตำแหน่งที่รูปแบบในข้อมูลมีการเปลี่ยนแปลงและขึ้นอยู่กับความเชี่ยวชาญด้านโดเมนของคุณ

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการงานทั่วไปอื่นๆ ใน R:

วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน R
วิธีดำเนินการถดถอยเอ็กซ์โปเนนเชียลใน R
วิธีดำเนินการถดถอยกำลังสองน้อยที่สุดแบบถ่วงน้ำหนักใน R