วิธีดำเนินการ ols regression ใน r (พร้อมตัวอย่าง)
การถดถอยกำลังสองน้อยที่สุดสามัญ (OLS) เป็นวิธีการที่ช่วยให้เราค้นหาเส้นที่อธิบายความสัมพันธ์ระหว่างตัวแปรทำนายหนึ่งตัวหรือมากกว่ากับ ตัวแปรตอบสนอง ได้ดีที่สุด
วิธีนี้ช่วยให้เราสามารถค้นหาสมการต่อไปนี้:
ŷ = ข 0 + ข 1 x
ทอง:
- ŷ : ค่าตอบกลับโดยประมาณ
- b 0 : ต้นกำเนิดของเส้นถดถอย
- b 1 : ความชันของเส้นถดถอย
สมการนี้สามารถช่วยให้เราเข้าใจความสัมพันธ์ระหว่างตัวทำนายและตัวแปรตอบสนอง และสามารถใช้เพื่อทำนายค่าของตัวแปรตอบสนองตามค่าของตัวแปรทำนายได้
ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีการดำเนินการถดถอย OLS ใน R
ขั้นตอนที่ 1: สร้างข้อมูล
สำหรับตัวอย่างนี้ เราจะสร้างชุดข้อมูลที่ประกอบด้วยตัวแปรสองตัวต่อไปนี้สำหรับนักเรียน 15 คน:
- จำนวนชั่วโมงเรียนทั้งหมด
- ผลสอบ
เราจะทำการถดถอย OLS โดยใช้ชั่วโมงเป็นตัวแปรทำนายและคะแนนสอบเป็นตัวแปรตอบสนอง
รหัสต่อไปนี้แสดงวิธีสร้างชุดข้อมูลปลอมใน R:
#create dataset df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14), score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89)) #view first six rows of dataset head(df) hours score 1 1 64 2 2 66 3 4 76 4 5 73 5 5 74 6 6 81
ขั้นตอนที่ 2: แสดงภาพข้อมูล
ก่อนที่จะดำเนินการถดถอย OLS เรามาสร้างแผนภาพกระจายเพื่อแสดงภาพความสัมพันธ์ระหว่างชั่วโมงและคะแนนสอบ:
library (ggplot2) #create scatterplot ggplot(df, aes(x=hours, y=score)) + geom_point(size= 2 )
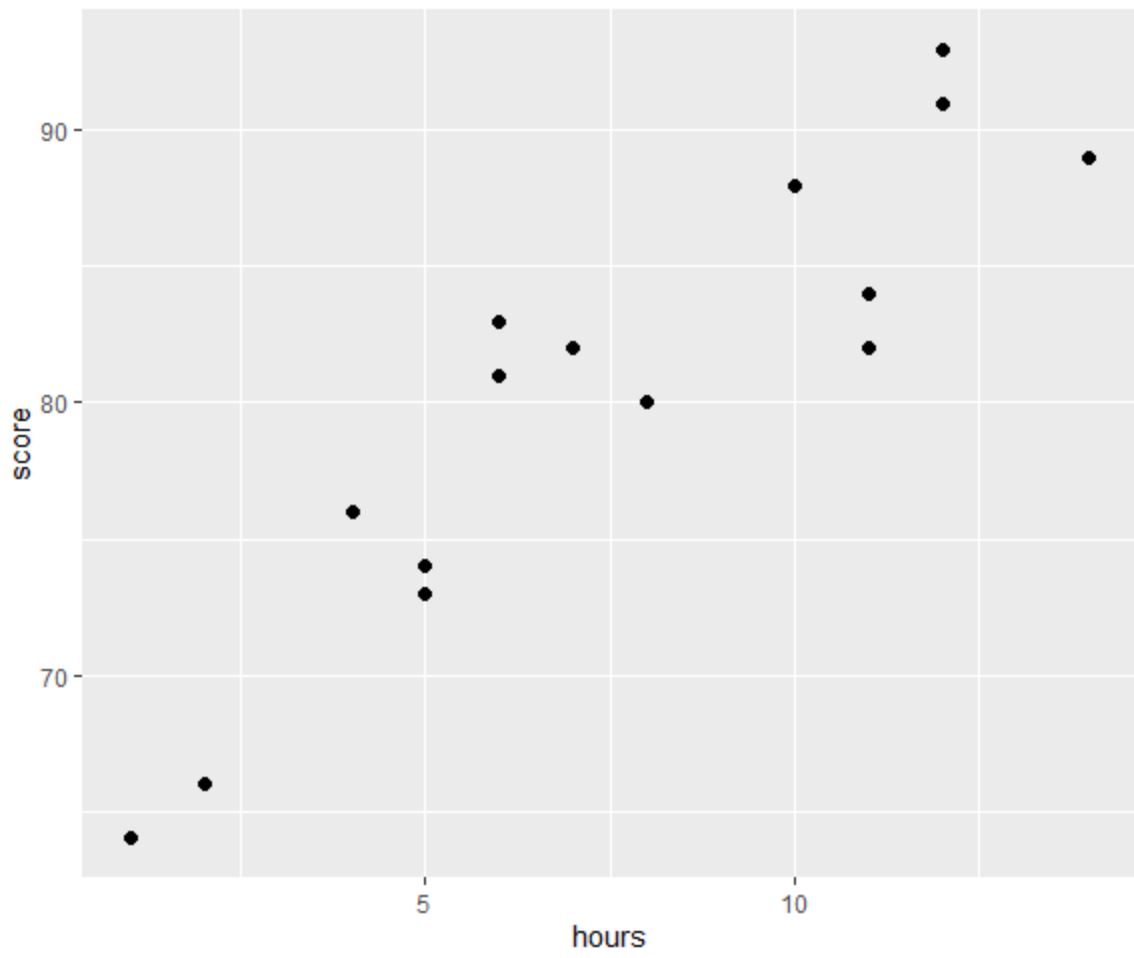
หนึ่งใน สี่สมมติฐาน ของการถดถอยเชิงเส้นคือมีความสัมพันธ์เชิงเส้นระหว่างตัวทำนายและตัวแปรตอบสนอง
จากกราฟเราจะเห็นว่าความสัมพันธ์มีลักษณะเป็นเส้นตรง เมื่อจำนวนชั่วโมงเพิ่มขึ้น คะแนนก็มีแนวโน้มที่จะเพิ่มขึ้นเป็นเส้นตรงเช่นกัน
จากนั้นเราสามารถสร้าง boxplot เพื่อแสดงภาพการกระจายของผลการสอบและตรวจสอบค่าผิดปกติ
หมายเหตุ : R นิยามการสังเกตว่าเป็นค่าผิดปกติ หากมีค่าเป็น 1.5 เท่าของพิสัยระหว่างควอร์ไทล์เหนือควอไทล์ที่ 3 หรือ 1.5 เท่าของพิสัยระหว่างควอไทล์ที่ต่ำกว่าควอไทล์ที่ 1
หากการสังเกตนั้นผิดปกติ วงกลมเล็กๆ จะปรากฏขึ้นใน boxplot:
library (ggplot2) #create scatterplot ggplot(df, aes(y=score)) + geom_boxplot()
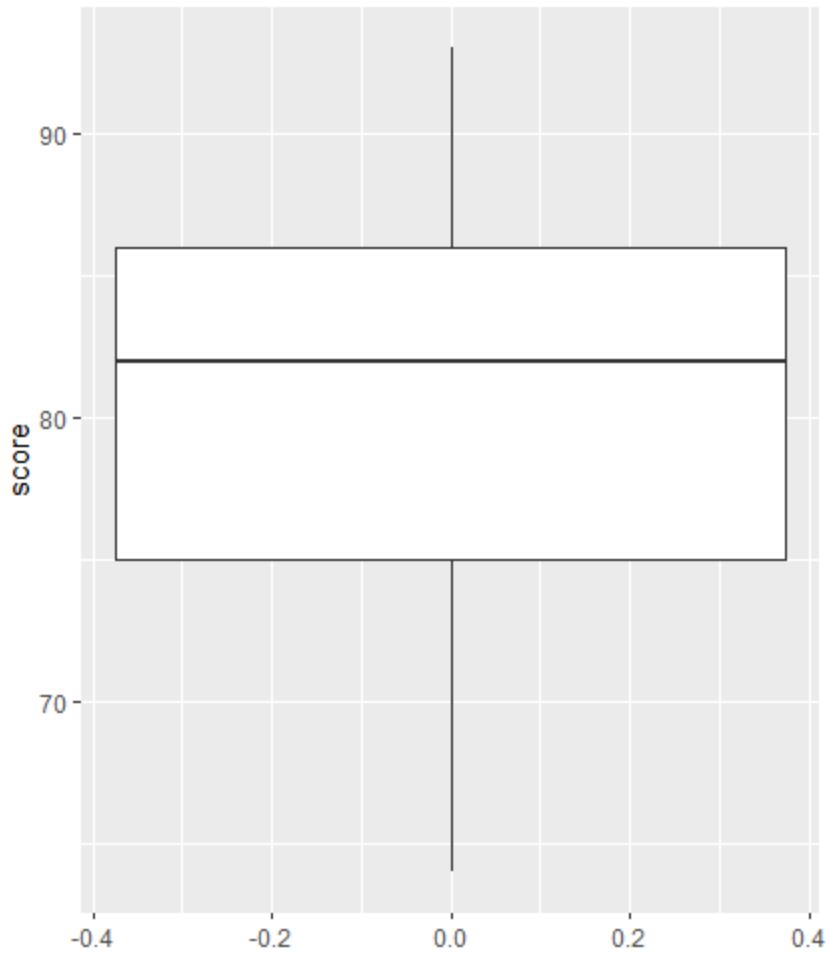
ไม่มีวงกลมเล็กๆ ใน boxplot ซึ่งหมายความว่าไม่มีค่าผิดปกติในชุดข้อมูลของเรา
ขั้นตอนที่ 3: ดำเนินการการถดถอย OLS
ต่อไป เราสามารถใช้ฟังก์ชัน lm() ใน R เพื่อดำเนินการถดถอย OLS โดยใช้ชั่วโมงเป็นตัวแปรทำนายและใช้คะแนนเป็นตัวแปรตอบสนอง:
#fit simple linear regression model model <- lm(score~hours, data=df) #view model summary summary(model) Call: lm(formula = score ~ hours) Residuals: Min 1Q Median 3Q Max -5,140 -3,219 -1,193 2,816 5,772 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 65,334 2,106 31,023 1.41e-13 *** hours 1.982 0.248 7.995 2.25e-06 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.641 on 13 degrees of freedom Multiple R-squared: 0.831, Adjusted R-squared: 0.818 F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06
จากสรุปแบบจำลอง เราจะเห็นว่าสมการถดถอยที่ติดตั้งคือ:
คะแนน = 65.334 + 1.982*(ชั่วโมง)
ซึ่งหมายความว่าแต่ละชั่วโมงที่เรียนเพิ่มเติมจะสัมพันธ์กับคะแนนสอบเฉลี่ยที่เพิ่มขึ้น 1,982 คะแนน
ค่าเดิมที่ 65,334 บอกเราถึงคะแนนสอบโดยเฉลี่ยที่คาดหวังสำหรับนักเรียนที่เรียนเป็นเวลา 0 ชั่วโมง
นอกจากนี้เรายังสามารถใช้สมการนี้เพื่อค้นหาคะแนนสอบที่คาดหวังโดยพิจารณาจากจำนวนชั่วโมงที่นักเรียนเรียน
เช่น นักเรียนที่เรียน 10 ชั่วโมง ควรได้คะแนนสอบ 85.15 :
คะแนน = 65.334 + 1.982*(10) = 85.15
ต่อไปนี้เป็นวิธีการตีความสรุปแบบจำลองที่เหลือ:
- Pr(>|t|): นี่คือค่า p ที่เกี่ยวข้องกับค่าสัมประสิทธิ์แบบจำลอง เนื่องจากค่า p สำหรับ ชั่วโมง (2.25e-06) น้อยกว่า 0.05 อย่างมีนัยสำคัญ เราจึงสามารถพูดได้ว่ามีความสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่าง ชั่วโมง และ คะแนน
- ค่า R-squared หลายตัว: ตัวเลขนี้บอกเราว่าเปอร์เซ็นต์ของความแปรผันของคะแนนสอบสามารถอธิบายได้ด้วยจำนวนชั่วโมงที่เรียน โดยทั่วไป ยิ่งค่า R-squared ของแบบจำลองการถดถอยมีค่ามากเท่าใด ตัวแปรทำนายก็จะทำนายค่าของตัวแปรตอบสนองได้ดีขึ้นเท่านั้น ในกรณีนี้ 83.1% ของความแปรผันของคะแนนสามารถอธิบายได้ด้วยจำนวนชั่วโมงที่ศึกษา
- ข้อผิดพลาดมาตรฐานที่เหลือ: นี่คือระยะห่างเฉลี่ยระหว่างค่าที่สังเกตได้และเส้นการถดถอย ยิ่งค่านี้ต่ำลง เส้นการถดถอยก็จะยิ่งสอดคล้องกับข้อมูลที่สังเกตได้มากขึ้นเท่านั้น ในกรณีนี้ คะแนนเฉลี่ยที่สังเกตได้ในการสอบจะเบี่ยงเบนไป 3,641 คะแนน จากคะแนนที่ทำนายด้วยเส้นถดถอย
- สถิติ F และค่า p: สถิติ F ( 63.91 ) และค่า p ที่สอดคล้องกัน ( 2.253e-06 ) บอกเราถึงความสำคัญโดยรวมของแบบจำลองการถดถอย กล่าวคือ ตัวแปรตัวทำนายในแบบจำลองนั้นมีประโยชน์ในการอธิบายการเปลี่ยนแปลงหรือไม่ . ในตัวแปรตอบสนอง เนื่องจากค่า p ในตัวอย่างนี้น้อยกว่า 0.05 แบบจำลองของเราจึงมีนัยสำคัญทางสถิติ และ ชั่วโมง จึงถือว่ามีประโยชน์ในการอธิบายความแปรผันของ คะแนน
ขั้นตอนที่ 4: สร้างแปลงที่เหลือ
สุดท้าย เราจำเป็นต้องสร้างแปลงที่เหลือเพื่อตรวจสอบสมมติฐานของ การรักร่วมเพศ และ ความเป็นปกติ
ข้อสันนิษฐานของ โฮโมสซิดาสติกซิตี คือ ส่วนที่เหลือ ของแบบจำลองการถดถอยมีความแปรปรวนเท่ากันโดยประมาณในแต่ละระดับของตัวแปรทำนาย
เพื่อตรวจสอบว่าเป็นไปตามสมมติฐานนี้ เราสามารถสร้าง พล็อตของค่าคงเหลือเทียบกับค่าพอดี ได้
แกน x จะแสดงค่าที่พอดี และแกน y จะแสดงค่าคงเหลือ ตราบใดที่ส่วนที่เหลือปรากฏว่ามีการกระจายแบบสุ่มและสม่ำเสมอทั่วทั้งกราฟรอบๆ ค่าศูนย์ เราสามารถสรุปได้ว่าความเป็นเนื้อเดียวกันจะไม่ถูกละเมิด:
#define residuals res <- resid(model) #produce residual vs. fitted plot plot(fitted(model), res) #add a horizontal line at 0 abline(0,0)
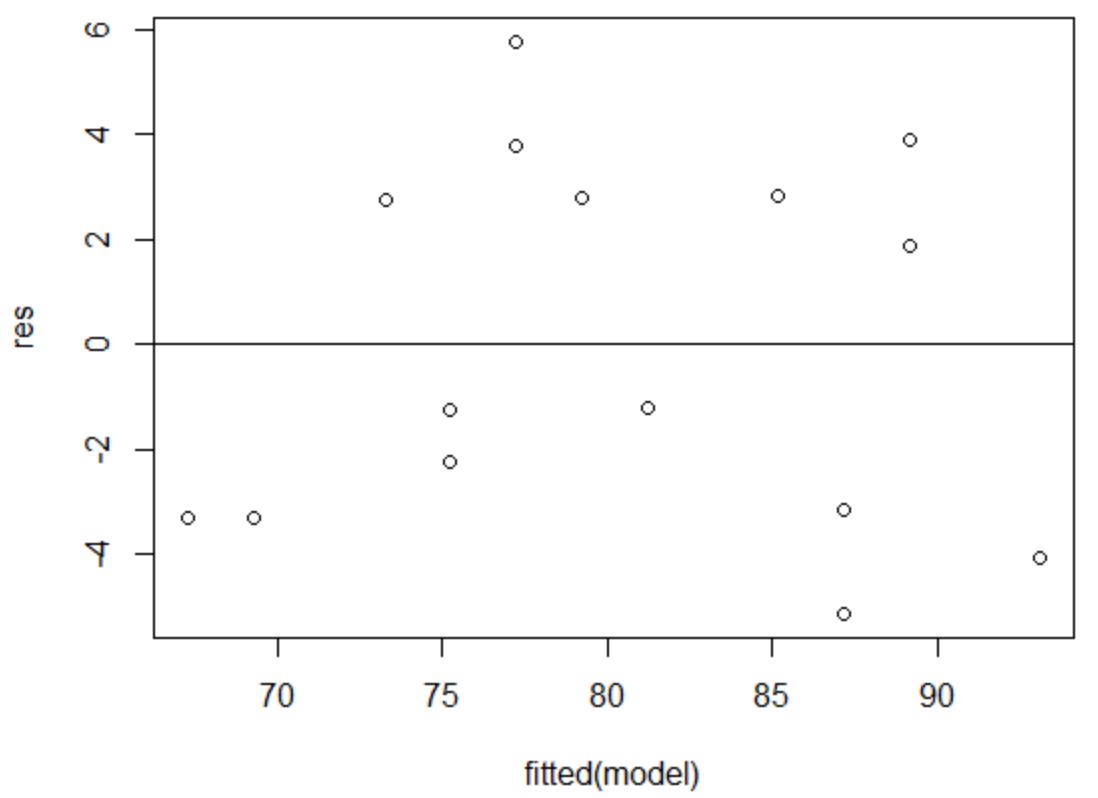
ส่วนที่เหลือดูเหมือนจะกระจัดกระจายแบบสุ่มรอบๆ ศูนย์ และไม่มีรูปแบบที่เห็นได้ชัดเจน ดังนั้นจึงเป็นไปตามสมมติฐานนี้
สมมติฐานภาวะ ปกติ ระบุว่า ส่วนที่เหลือ ของแบบจำลองการถดถอยมีการกระจายตามปกติโดยประมาณ
เพื่อตรวจสอบว่าเป็นไปตามสมมติฐานนี้หรือไม่ เราสามารถสร้าง พล็อต QQ หากจุดลงจุดอยู่ตามแนวเส้นตรงประมาณ 45 องศา ข้อมูลก็จะมีการกระจายตามปกติ:
#create QQ plot for residuals qqnorm(res) #add a straight diagonal line to the plot qqline(res)
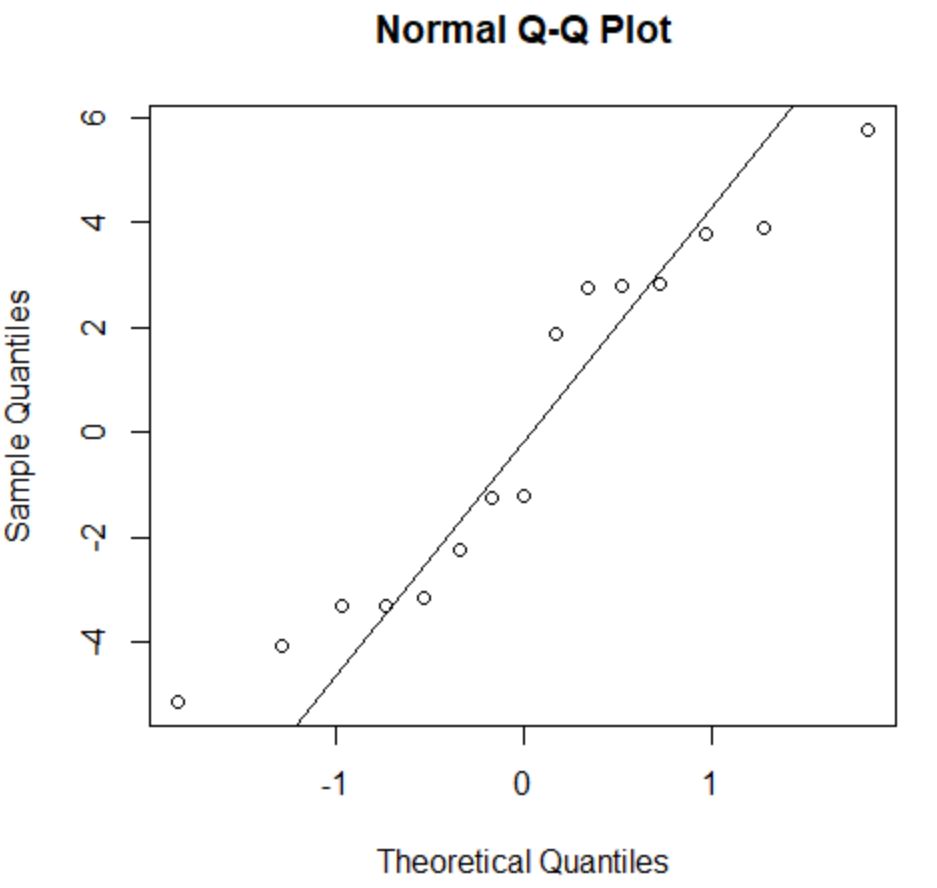
สารตกค้างเบี่ยงเบนไปจากเส้น 45 องศาเล็กน้อย แต่ไม่มากพอที่จะทำให้เกิดความกังวลร้ายแรง เราสามารถสรุปได้ว่าเป็นไปตามสมมติฐานปกติ
เนื่องจากส่วนที่เหลือมีการกระจายตามปกติและเป็นโฮโมสเคดาสติก เราจึงตรวจสอบได้ว่าเป็นไปตามสมมติฐานของแบบจำลองการถดถอย OLS
ดังนั้นผลลัพธ์ของแบบจำลองของเราจึงมีความน่าเชื่อถือ
หมายเหตุ : หากไม่เป็นไปตามสมมติฐานตั้งแต่หนึ่งข้อขึ้นไป เราอาจพยายาม แปลง ข้อมูลของเรา
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการงานทั่วไปอื่นๆ ใน R:
วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน R
วิธีดำเนินการถดถอยเอ็กซ์โปเนนเชียลใน R
วิธีดำเนินการถดถอยกำลังสองน้อยที่สุดแบบถ่วงน้ำหนักใน R