รู้เบื้องต้นเกี่ยวกับการถดถอยแบบ lasso

ใน การถดถอยเชิงเส้นพหุคูณ แบบธรรมดา เราใช้ชุดของตัวแปรทำนาย p และ ตัวแปรตอบสนอง เพื่อให้พอดีกับแบบจำลองของรูปแบบ:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

ทอง:

• Y : ตัวแปรตอบสนอง
• X _j : ^{ตัวแปร} ทำนายที่ j
• β _j : ผลกระทบโดยเฉลี่ยต่อ Y ของการเพิ่มขึ้นของ X _j หนึ่งหน่วย โดยคงตัวทำนายอื่นๆ ทั้งหมดไว้คงที่
• ε : เงื่อนไขข้อผิดพลาด

ค่าของ β ₀ , β ₁ , B ₂ , …, β _p ถูกเลือกโดยใช้ วิธีกำลังสองน้อยที่สุด ซึ่งจะลดผลรวมของกำลังสองของส่วนที่เหลือ (RSS):

RSS = Σ(ฉัน _ฉัน – ŷ _ฉัน ) ²

ทอง:

• Σ : สัญลักษณ์กรีกหมายถึง ผลรวม
• y _i : ค่าตอบสนองจริงสำหรับการสังเกต ^{ครั้งที่ 3}
• ŷ _i : ค่าตอบสนองที่คาดการณ์ไว้ตามแบบจำลองการถดถอยเชิงเส้นพหุคูณ

อย่างไรก็ตาม เมื่อตัวแปรทำนายมีความสัมพันธ์กันสูง ความเป็นหลายคอลลิเนียร์ อาจกลายเป็นปัญหาได้ ซึ่งอาจทำให้การประมาณค่าสัมประสิทธิ์แบบจำลองไม่น่าเชื่อถือและแสดงความแปรปรวนสูง กล่าวคือ เมื่อนำแบบจำลองไปใช้กับชุดข้อมูลใหม่ที่ไม่เคยเห็นมาก่อน ก็มีแนวโน้มว่าจะทำงานได้ไม่ดี

วิธีหนึ่งในการแก้ไขปัญหานี้คือการใช้วิธีการที่เรียกว่า Lasso Regression ซึ่งพยายามลดสิ่งต่อไปนี้ให้เหลือน้อยที่สุด:

RSS + ΣΣ|β _j |

โดยที่ j ไปจาก 1 ถึง p และ แล ≥ 0

เทอมที่สองในสมการนี้เรียกว่า การลงโทษการถอน

เมื่อ แล = 0 เงื่อนไขการลงโทษนี้ไม่มีผลใดๆ และการถดถอยแบบ Lasso จะให้ค่าประมาณค่าสัมประสิทธิ์เท่ากับกำลังสองน้อยที่สุด

อย่างไรก็ตาม เมื่อ แล เข้าใกล้อนันต์ การลงโทษการลบออกจะมีอิทธิพลมากขึ้น และตัวแปรทำนายที่ไม่สามารถนำเข้าลงในโมเดลได้จะลดลงเหลือศูนย์ และบางส่วนก็ถูกลบออกจากโมเดลด้วยซ้ำ

เหตุใดจึงใช้การถดถอยแบบ Lasso

ข้อดีของการถดถอยแบบบ่วงบาศเหนือการถดถอยกำลังสองน้อยที่สุดคือ การแลกเปลี่ยนความแปรปรวนอคติ

โปรดจำไว้ว่า Mean Square Error (MSE) เป็นหน่วยเมตริกที่เราสามารถใช้เพื่อวัดความแม่นยำของแบบจำลองที่กำหนด และมีการคำนวณดังนี้

MSE = วาร์( f̂( x ₀ )) + [อคติ( f̂( x ₀ ))] ² + วาร์(ε)

MSE = ความแปรปรวน + อคติ ² + ข้อผิดพลาดที่ลดไม่ได้

แนวคิดพื้นฐานของการถดถอยแบบบ่วงบาศคือการแนะนำอคติเล็กน้อยเพื่อลดความแปรปรวนลงอย่างมาก ส่งผลให้ MSE โดยรวมลดลง

เพื่ออธิบายสิ่งนี้ ให้พิจารณากราฟต่อไปนี้:

โปรดทราบว่าเมื่อ แล เพิ่มขึ้น ความแปรปรวนจะลดลงอย่างมีนัยสำคัญโดยมีอคติเพิ่มขึ้นเล็กน้อย อย่างไรก็ตาม เมื่อเกินจุดใดจุดหนึ่ง ความแปรปรวนจะลดลงอย่างรวดเร็วน้อยลง และการลดลงของค่าสัมประสิทธิ์นำไปสู่การประเมินค่าเหล่านี้ต่ำเกินไปอย่างมีนัยสำคัญ ซึ่งนำไปสู่การเพิ่มขึ้นอย่างมากในอคติ

จากกราฟเราจะเห็นได้ว่า MSE ของการทดสอบนั้นต่ำที่สุด เมื่อเราเลือกค่าสำหรับ γ ที่สร้างการแลกเปลี่ยนที่เหมาะสมที่สุดระหว่างอคติและความแปรปรวน

เมื่อ แล = 0 เงื่อนไขการลงโทษในการถดถอยแบบบ่วงบาศจะไม่มีผลใดๆ ดังนั้นจึงให้ค่าประมาณค่าสัมประสิทธิ์เดียวกันกับกำลังสองน้อยที่สุด อย่างไรก็ตาม การเพิ่ม แล ถึงจุดหนึ่งจะทำให้ค่า MSE โดยรวมของการทดสอบลดลงได้

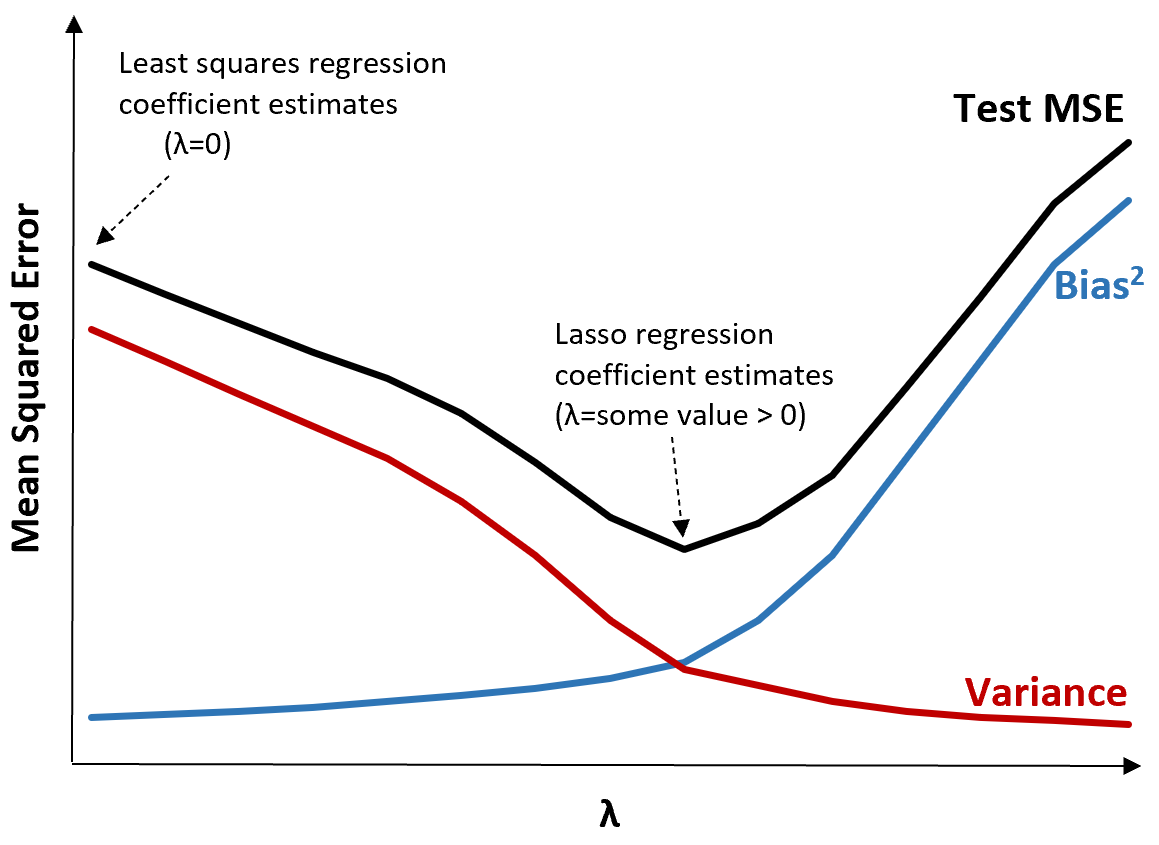
ซึ่งหมายความว่าการปรับโมเดลให้เหมาะสมด้วยการถดถอยแบบบ่วงบาศจะทำให้เกิดข้อผิดพลาดในการทดสอบน้อยกว่าการปรับโมเดลให้เหมาะสมด้วยการถดถอยกำลังสองน้อยที่สุด

การถดถอยแบบ Lasso เทียบกับการถดถอยแบบ Ridge

Lasso regression และ Ridge regression รู้จักกันในชื่อ วิธีการทำให้เป็นมาตรฐาน เนื่องจากทั้งสองพยายามลดผลรวมที่เหลือของกำลังสอง (RSS) ให้เหลือน้อยที่สุด รวมถึงการลงโทษด้วย

กล่าวอีกนัยหนึ่ง พวกมันจำกัดหรือทำให้การประมาณค่าสัมประสิทธิ์แบบจำลอง เป็นปกติ

อย่างไรก็ตาม เงื่อนไขการลงโทษที่พวกเขาใช้แตกต่างกันเล็กน้อย:

• การถดถอยแบบ Lasso พยายามย่อ ขนาด RSS + ΣΣ|β _j | ให้เหลือน้อยที่สุด
• การถดถอยแบบริดจ์พยายามย่อ ขนาด RSS + ΣΣβ _j ² ให้เหลือน้อยที่สุด

เมื่อเราใช้การถดถอยแบบสัน ค่าสัมประสิทธิ์ของตัวทำนายแต่ละตัวจะลดลงเหลือศูนย์ แต่ไม่มีตัวใดที่สามารถไป ถึงศูนย์ได้อย่างสมบูรณ์

ในทางกลับกัน เมื่อเราใช้การถดถอยแบบบ่วงบาศ อาจเป็นไปได้ที่สัมประสิทธิ์บางส่วนจะกลาย เป็นศูนย์โดยสมบูรณ์ เมื่อ แล มีขนาดใหญ่เพียงพอ

ในแง่เทคนิค การถดถอยแบบบ่วงบาศสามารถสร้างแบบจำลอง “กระจัดกระจาย” ซึ่งก็คือแบบจำลองที่มีเฉพาะตัวแปรตัวทำนายเพียงชุดย่อยเท่านั้น

สิ่งนี้ทำให้เกิดคำถาม: การถดถอยแบบสันหรือการถดถอยแบบบ่วงบาศดีกว่าหรือไม่

คำตอบ: มันขึ้นอยู่กับ!

ในกรณีที่ตัวแปรทำนายจำนวนเล็กน้อยมีความสำคัญ การถดถอยแบบเชือกมีแนวโน้มที่จะทำงานได้ดีขึ้น เนื่องจากสามารถลดตัวแปรที่ไม่มีนัยสำคัญให้เหลือศูนย์และลบตัวแปรเหล่านั้นออกจากแบบจำลองได้

อย่างไรก็ตาม เมื่อตัวแปรทำนายจำนวนมากมีนัยสำคัญในแบบจำลองและค่าสัมประสิทธิ์ของตัวแปรมีค่าเท่ากันโดยประมาณ การถดถอยแบบสันมีแนวโน้มที่จะทำงานได้ดีขึ้น เนื่องจากจะเก็บตัวทำนายทั้งหมดไว้ในแบบจำลอง

เพื่อพิจารณาว่าโมเดลใดมีประสิทธิภาพมากที่สุดในการคาดการณ์ เราทำการ ตรวจสอบความถูกต้องข้าม k-fold ไม่ว่ารุ่นใดจะทำให้เกิดค่าคลาดเคลื่อนกำลังสองเฉลี่ยต่ำสุด (MSE) ก็เป็นรุ่นที่ดีที่สุดที่จะใช้

ขั้นตอนในการถดถอยแบบบ่วงบาศในทางปฏิบัติ

ขั้นตอนต่อไปนี้สามารถใช้เพื่อดำเนินการถดถอยแบบบ่วงบาศ:

ขั้นตอนที่ 1: คำนวณเมทริกซ์สหสัมพันธ์และค่า VIF สำหรับตัวแปรทำนาย

ขั้นแรก เราต้องสร้าง เมทริกซ์สหสัมพันธ์ และคำนวณ ค่า VIF (ปัจจัยอัตราเงินเฟ้อแปรปรวน) สำหรับตัวแปรทำนายแต่ละตัว

หากเราตรวจพบความสัมพันธ์ที่ชัดเจนระหว่างตัวแปรทำนายและค่า VIF สูง (ข้อความบางข้อความกำหนดค่า VIF “สูง” เป็น 5 ในขณะที่ข้อความอื่นใช้ 10) การถดถอยแบบ Lasso อาจเหมาะสม

อย่างไรก็ตาม หากข้อมูลไม่มีหลายคอลลิเนียริตี้ ก็อาจไม่จำเป็นต้องทำการถดถอยแบบบ่วงบาศตั้งแต่แรก แต่เราสามารถใช้การถดถอยกำลังสองน้อยที่สุดแบบธรรมดาแทนได้

ขั้นตอนที่ 2: ปรับโมเดลการถดถอยแบบ Lasso และเลือกค่าสำหรับ แล

เมื่อเราพิจารณาแล้วว่าการถดถอยแบบบ่วงบาศมีความเหมาะสม เราก็จะสามารถปรับโมเดลให้เหมาะสมได้ (โดยใช้ภาษาการเขียนโปรแกรมยอดนิยม เช่น R หรือ Python) โดยใช้ค่าที่เหมาะสมที่สุดสำหรับ แล

เพื่อกำหนดค่าที่เหมาะสมที่สุดสำหรับ แล เราสามารถใส่โมเดลหลาย ๆ แบบโดยใช้ค่าที่แตกต่างกันสำหรับ แลม และเลือก แล เป็นค่าที่สร้างการทดสอบ MSE ที่ต่ำที่สุด

ขั้นตอนที่ 3: เปรียบเทียบการถดถอยแบบบ่วงบาศกับการถดถอยแบบสันและการถดถอยกำลังสองน้อยที่สุดสามัญ

สุดท้ายนี้ เราสามารถเปรียบเทียบแบบจำลองการถดถอยแบบบ่วงบาศกับแบบจำลองการถดถอยแบบสันและแบบจำลองการถดถอยกำลังสองน้อยที่สุดเพื่อพิจารณาว่าแบบจำลองใดที่สร้างการทดสอบ MSE ต่ำสุดโดยใช้การตรวจสอบความถูกต้องข้ามแบบ k-fold

ขึ้นอยู่กับความสัมพันธ์ระหว่างตัวแปรทำนายและตัวแปรตอบสนอง มีความเป็นไปได้โดยสิ้นเชิงว่าหนึ่งในสามโมเดลนี้จะมีประสิทธิภาพเหนือกว่าโมเดลอื่นๆ ในสถานการณ์ที่แตกต่างกัน

การถดถอยแบบ Lasso ใน R & Python

บทช่วยสอนต่อไปนี้จะอธิบายวิธีการถดถอยแบบ Lasso ใน R และ Python:

Lasso Regression ใน R (ทีละขั้นตอน)
Lasso Regression ใน Python (ทีละขั้นตอน)