การถดถอยโลจิสติก

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 2, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการถดถอยโลจิสติกในสถิติคืออะไร ในทำนองเดียวกัน คุณจะพบสูตรการถดถอยโลจิสติก ประเภทต่างๆ ของการถดถอยโลจิสติก และยิ่งกว่านั้น แบบฝึกหัดการถดถอยโลจิสติกที่แก้ไขแล้ว

การถดถอยโลจิสติกคืออะไร?

ในสถิติ การถดถอยโลจิสติก เป็นรูปแบบหนึ่งของแบบจำลองการถดถอยที่ใช้ในการทำนายผลลัพธ์ของ ตัวแปรเชิงหมวดหมู่ นั่นคือ การถดถอยโลจิสติกใช้ในการจำลองความน่าจะเป็นที่ตัวแปรเชิงหมวดหมู่ใช้กับค่าที่กำหนดโดยอิงจากตัวแปรอิสระ

แบบจำลองการถดถอยโลจิสติกที่พบบ่อยที่สุดคือการถดถอยโลจิสติกแบบไบนารี ซึ่งมีเพียงสองผลลัพธ์ที่เป็นไปได้: “ความล้มเหลว” หรือ “ความสำเร็จ” ( การแจกแจงแบบแบร์นูลลี ) “ความล้มเหลว” แสดงด้วยค่า 0 ในขณะที่ “ความสำเร็จ” แสดงด้วยค่า 1

ตัวอย่างเช่น ความน่าจะเป็นที่นักเรียนจะสอบผ่านโดยอิงตามชั่วโมงที่พวกเขาใช้เวลาเรียนสามารถศึกษาได้โดยใช้แบบจำลองการถดถอยลอจิสติก ในกรณีนี้ ความล้มเหลวจะเป็นผลมาจาก “ความล้มเหลว” และในทางกลับกัน ความสำเร็จจะเป็นผลมาจาก “ความสำเร็จ”

สูตรการถดถอยโลจิสติก

สมการสำหรับแบบจำลองการถดถอยโลจิสติกคือ:

$\displaystyle \ln \left(\frac{p}{1-p}\right) =\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i$

ดังนั้น ในแบบจำลองการถดถอยโลจิสติก ความน่าจะเป็นที่จะได้รับผลลัพธ์ “ความสำเร็จ” นั่นคือตัวแปรตามรับค่า 1 จะถูกคำนวณด้วยสูตรต่อไปนี้:

$p=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}$

ทอง:

$p$

คือความน่าจะเป็นที่ตัวแปรตามคือ 1
$\beta_0$

คือค่าคงที่ของแบบจำลองการถดถอยโลจิสติก
$\beta_i$

คือสัมประสิทธิ์การถดถอยของตัวแปร i
$x_i$

คือค่าของตัวแปร i

ตัวอย่างแบบจำลองการถดถอยโลจิสติก

ตอนนี้เรารู้คำจำกัดความของการถดถอยลอจิสติกแล้ว เรามาดูตัวอย่างที่ชัดเจนของวิธีการสร้างแบบจำลองของการถดถอยประเภทนี้กัน

ในตารางต่อไปนี้ มีการรวบรวมข้อมูล 20 ชุดที่เกี่ยวข้องกับชั่วโมงเรียนของนักเรียนแต่ละคน และไม่ว่าพวกเขาจะผ่านหรือไม่ผ่านการทดสอบสถิติ เรียกใช้แบบจำลองการถดถอยลอจิสติกส์และคำนวณความน่าจะเป็นที่นักเรียนจะผ่านหากเขาหรือเธอเรียนเป็นเวลา 4 ชั่วโมง

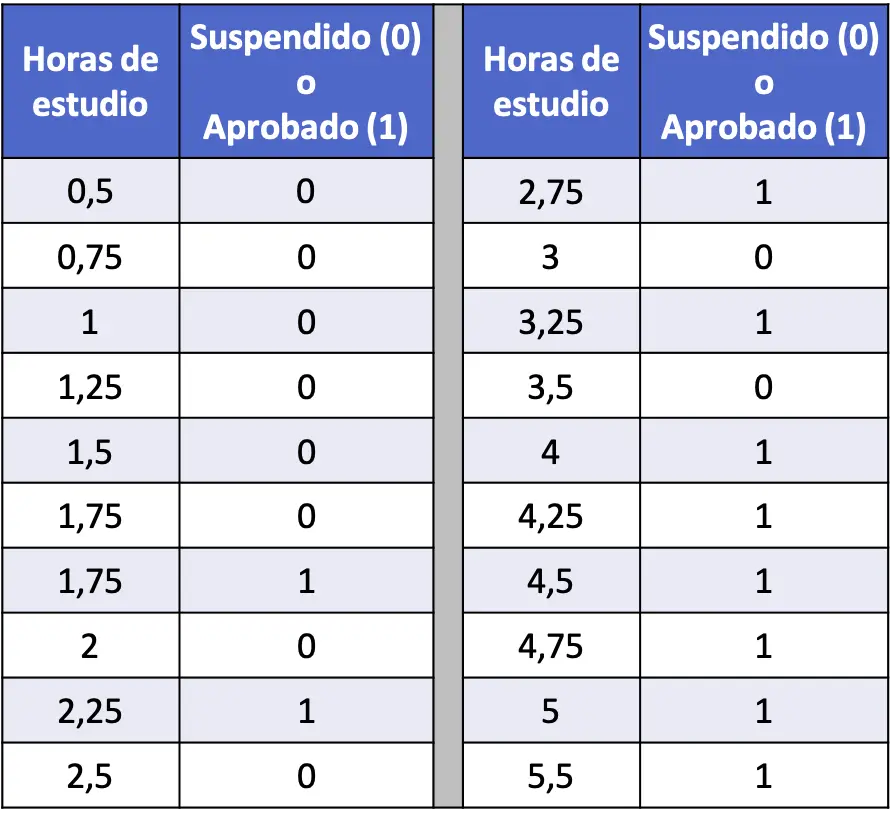
ในกรณีนี้ ตัวแปรอธิบายคือจำนวนชั่วโมงเรียน และตัวแปรตอบกลับคือนักเรียนสอบไม่ผ่าน (0) หรือผ่าน (1) ดังนั้นในแบบจำลองของเราเราจะมีเพียงค่าสัมประสิทธิ์เท่านั้น

$\beta_0$

และค่าสัมประสิทธิ์

$\beta_1$

เนื่องจากมีตัวแปรอิสระเพียงตัวเดียวเท่านั้น

$\beta_0 \qquad \beta_1$

การหาค่าสัมประสิทธิ์การถดถอยด้วยตนเองนั้นต้องใช้ความพยายามอย่างมาก ดังนั้นจึงแนะนำให้ใช้ซอฟต์แวร์คอมพิวเตอร์ เช่น Minitab ดังนั้นค่าสัมประสิทธิ์การถดถอยที่คำนวณโดยใช้ Minitab จึงเป็นดังนี้

$\begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}$

แบบจำลองการถดถอยโลจิสติกจึงเป็นดังนี้:

$\begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}$

ด้านล่างนี้ คุณสามารถดูข้อมูลตัวอย่างและสมการแบบจำลองการถดถอยโลจิสติกที่แสดงเป็นกราฟ:

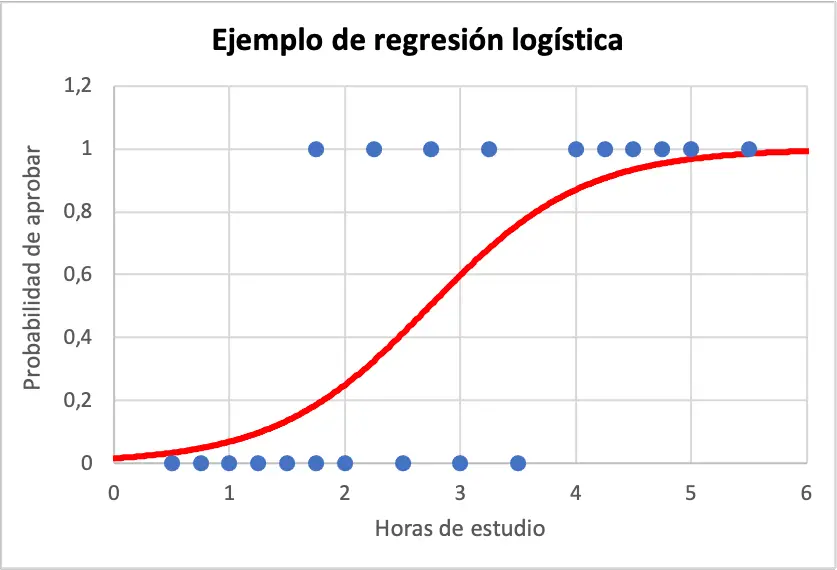
ดังนั้น ในการคำนวณความน่าจะเป็นที่นักเรียนจะประสบความสำเร็จหากเรียนไป 4 ชั่วโมง ให้ใช้สมการที่ได้จากแบบจำลองการถดถอยลอจิสติก:

$\begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}$

สรุปคือ ถ้านักเรียนเรียนสี่ชั่วโมงจะมีโอกาสสอบผ่าน 86.99%

ประเภทของการถดถอยโลจิสติก

การถดถอยโลจิสติกมีสามประเภท :

Binary Logistic Regression : ตัวแปรตามสามารถมีได้เพียงสองค่าเท่านั้น (0 และ 1)
การถดถอยโลจิสติกพหุนาม : ตัวแปรตามมีค่าที่เป็นไปได้มากกว่าสองค่า
การถดถอยโลจิสติกลำดับ : ผลลัพธ์ที่เป็นไปได้มีลำดับตามธรรมชาติ

การถดถอยโลจิสติกและการถดถอยเชิงเส้น

โดยสรุป เราจะเห็นว่าอะไรคือความแตกต่างระหว่างการถดถอยโลจิสติกและการถดถอยเชิงเส้น เนื่องจากแบบจำลองการถดถอยที่ใช้มากที่สุดในสถิติคือแบบจำลองเชิงเส้น

การถดถอยเชิงเส้น ใช้ในการจำลองตัวแปรตามตัวเลข นอกจากนี้ ในการถดถอยเชิงเส้น ความสัมพันธ์ระหว่างตัวแปรอธิบายและตัวแปรตอบสนองจะเป็นเชิงเส้น

ดังนั้น ความแตกต่างที่สำคัญระหว่างการถดถอยโลจิสติกและการถดถอยเชิงเส้น คือประเภทของตัวแปรตาม ในการถดถอยโลจิสติก ตัวแปรตามจะเป็นแบบหมวดหมู่ ในขณะที่ตัวแปรตามในการถดถอยเชิงเส้นจะเป็นตัวเลข

ดังนั้น การถดถอยโลจิสติกจึงถูกนำมาใช้เพื่อทำนายผลลัพธ์ระหว่างสองตัวเลือกที่เป็นไปได้ ในขณะที่การถดถอยเชิงเส้นจะช่วยทำนายผลลัพธ์ที่เป็นตัวเลข

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม