วิธีดำเนินการทดสอบ z สองสัดส่วนใน sas
การทดสอบค่า z แบบสองสัดส่วน ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างสัดส่วนประชากรสองสัดส่วนหรือไม่
การทดสอบนี้ใช้สมมติฐานว่างต่อไปนี้:
- H 0 : μ 1 = μ 2 (สัดส่วนประชากรทั้งสองเท่ากัน)
สมมติฐานทางเลือกอาจเป็นแบบทวิภาคี ซ้าย หรือขวา:
- H 1 (สองด้าน): π 1 ≠ π 2 (สัดส่วนประชากรทั้งสองไม่เท่ากัน)
- H 1 (ซ้าย): π 1 < π 2 (สัดส่วนประชากร 1 น้อยกว่าสัดส่วนประชากร 2)
- H 1 (ขวา): π 1 > π 2 (สัดส่วนประชากร 1 มากกว่าสัดส่วนประชากร 2)
เราใช้สูตรต่อไปนี้เพื่อคำนวณสถิติการทดสอบ z:
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
โดยที่ p 1 และ p 2 คือสัดส่วนตัวอย่าง n 1 และ n 2 คือขนาดตัวอย่าง และโดยที่ p คือสัดส่วนรวมรวมที่คำนวณได้ดังนี้:
พี = (พี 1 n 1 + พี 2 n 2 )/( n 1 + n 2 )
หากค่า p ที่สอดคล้องกับสถิติการทดสอบ z น้อยกว่าระดับนัยสำคัญที่เลือก (ตัวเลือกทั่วไปคือ 0.10, 0.05 และ 0.01) คุณสามารถปฏิเสธสมมติฐานว่างได้
ตัวอย่างต่อไปนี้แสดงวิธีดำเนินการทดสอบ z แบบสองสัดส่วนใน SAS
ตัวอย่าง: การทดสอบ Z สัดส่วนสองรายการใน SAS
สมมติว่าเราต้องการทราบว่ามีความแตกต่างระหว่างสัดส่วนของผู้อยู่อาศัยที่สนับสนุนกฎหมายบางอย่างในเคาน์ตี A และสัดส่วนที่สนับสนุนกฎหมายในเคาน์ตี B หรือไม่
เพื่อทดสอบสิ่งนี้ เราสุ่มตัวอย่างผู้อยู่อาศัย 50 คนจากแต่ละเคาน์ตี และนับจำนวนคนที่สนับสนุนกฎหมาย
รหัสต่อไปนี้แสดงวิธีสร้างชุดข้อมูลที่สรุปจำนวนผู้อยู่อาศัยที่สนับสนุนกฎหมายในแต่ละเคาน์ตี:
/*create dataset*/ data my_data; input county $status $count; datalines ; A Bracket 34 A Reject 16 B Bracket 29 B Reject 21 ; run ; /*view dataset*/ proc print data =my_data;
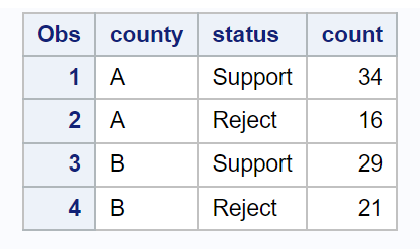
จากนั้นเราสามารถใช้คำสั่ง PROC FREQ กับตัวเลือก Riskdiff (เท่ากับ var = null) เพื่อทำการทดสอบ z สองสัดส่วน:
/*perform two proportion z-test*/
proc freq data =my_data;
weightcount ;
county tables * status / riskdiff ( equal var = null);
run ;
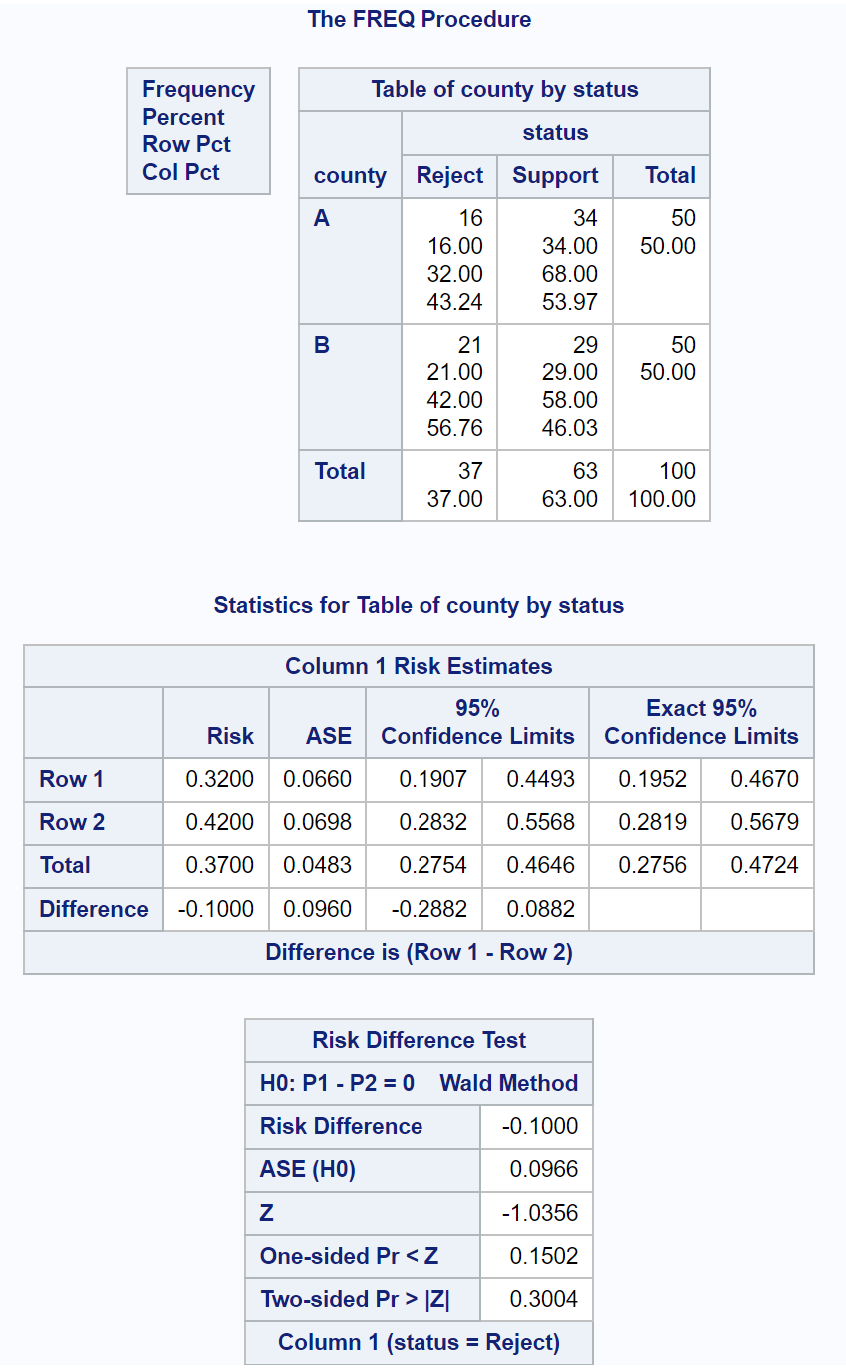
จาก การทดสอบความแตกต่างความเสี่ยง ในตารางผลลัพธ์ เราจะเห็นข้อมูลต่อไปนี้:
- สถิติการทดสอบ Z: -1.0356
- ค่า p สองด้าน: 0.3004
การทดสอบค่า z แบบสองสัดส่วนนี้ใช้สมมติฐานต่อไปนี้:
- H 0 : π 1 = π 2 (สัดส่วนประชากรทั้งสองเท่ากัน)
- H 1 : π 1 ≠ π 2 (สัดส่วนประชากรทั้งสองไม่เท่ากัน)
เนื่องจากค่า p ในเอาต์พุตไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้
ซึ่งหมายความว่าเราไม่มีหลักฐานเพียงพอที่จะกล่าวว่าสัดส่วนของผู้อยู่อาศัยที่สนับสนุนกฎหมายนี้แตกต่างกันระหว่างสองมณฑล
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการทดสอบทางสถิติทั่วไปอื่นๆ ใน SAS:
วิธีดำเนินการทดสอบ t-test หนึ่งตัวอย่างใน SAS
วิธีดำเนินการทดสอบทีสองตัวอย่างใน SAS
วิธีดำเนินการทดสอบตัวอย่างแบบจับคู่ใน SAS