วิธีการทดสอบความสัมพันธ์ใน r (พร้อมตัวอย่าง)

วิธีหนึ่งในการหาปริมาณความสัมพันธ์ระหว่างตัวแปรสองตัวคือการใช้ สัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน ซึ่ง เป็นหน่วยวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว

จะใช้ค่าระหว่าง -1 ถึง 1 เสมอโดยที่:

• -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
• 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
• 1 บ่งชี้ความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรสองตัว

หากต้องการทราบว่าสัมประสิทธิ์สหสัมพันธ์มีนัยสำคัญทางสถิติหรือไม่ คุณสามารถคำนวณคะแนน t และค่า p ที่สอดคล้องกันได้

สูตรคำนวณค่า t-score ของสัมประสิทธิ์สหสัมพันธ์ (r) คือ:

เสื้อ = r * √ n-2 / √ 1-r ²

ค่า p จะคำนวณเป็นค่า p สองด้านที่สอดคล้องกันสำหรับการแจกแจงแบบ t โดยมีดีกรีอิสระ n-2

ตัวอย่าง: การทดสอบความสัมพันธ์ใน R

เพื่อตรวจสอบว่าค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรสองตัวมีนัยสำคัญทางสถิติหรือไม่ คุณสามารถทำการทดสอบสหสัมพันธ์ใน R โดยใช้ไวยากรณ์ต่อไปนี้:

cor.test(x, y, method=c(“เพียร์สัน”, “เคนดัลล์”, “หอก”))

ทอง:

• x, y: เวกเตอร์ข้อมูลดิจิทัล
• วิธีการ: วิธีที่ใช้ในการคำนวณความสัมพันธ์ระหว่างเวกเตอร์สองตัว ค่าเริ่มต้นคือ “เพียร์สัน”

ตัวอย่างเช่น สมมติว่าเรามีเวกเตอร์สองตัวต่อไปนี้ใน R:

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

ก่อนที่จะทำการทดสอบความสัมพันธ์ระหว่างตัวแปรทั้งสอง เราสามารถสร้างแผนภาพกระจายอย่างรวดเร็วเพื่อแสดงความสัมพันธ์เป็นภาพได้:

 #create scatterplot
plot(x, y, pch= 16 )

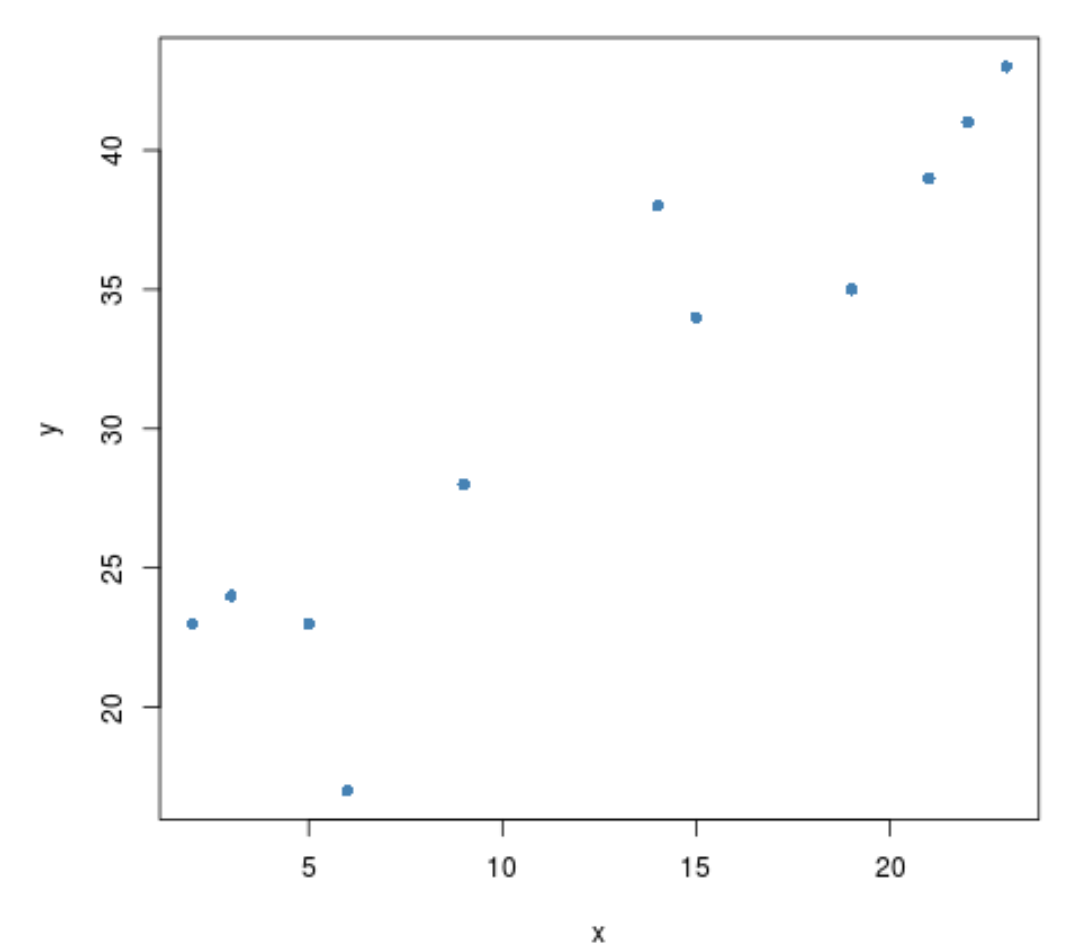
ดูเหมือนจะมีความสัมพันธ์เชิงบวกระหว่างตัวแปรทั้งสอง นั่นคือเมื่อคนหนึ่งเพิ่มขึ้น อีกคนก็มีแนวโน้มที่จะเพิ่มขึ้นเช่นกัน

หากต้องการดูว่าความสัมพันธ์นี้มีนัยสำคัญทางสถิติหรือไม่ เราสามารถทำการทดสอบความสัมพันธ์ได้:

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างเวกเตอร์ทั้งสองกลายเป็น 0.9279869 .

สถิติการทดสอบกลายเป็น 7.8756 และค่า p ที่สอดคล้องกันคือ 1.35e-05

เนื่องจากค่านี้น้อยกว่า 0.05 เราจึงมีหลักฐานเพียงพอที่จะกล่าวว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองมีนัยสำคัญทางสถิติ

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับค่าสัมประสิทธิ์สหสัมพันธ์:

ความรู้เบื้องต้นเกี่ยวกับสัมประสิทธิ์สหสัมพันธ์เพียร์สัน
อะไรคือความสัมพันธ์ที่ “แข็งแกร่ง”?
สมมติฐานทั้งห้าข้อเกี่ยวกับความสัมพันธ์ของเพียร์สัน