วิธีการทดสอบความเป็นอิสระของ chi-square ใน excel
การทดสอบความเป็นอิสระของไคสแควร์ ใช้เพื่อพิจารณาว่ามีความสัมพันธ์ที่มีนัยสำคัญระหว่างตัวแปรหมวดหมู่สองตัวหรือไม่
บทช่วยสอนนี้จะอธิบายวิธีการทดสอบความเป็นอิสระของไคสแควร์ใน Excel
ตัวอย่าง: การทดสอบอิสรภาพของ Chi-Square ใน Excel
สมมติว่าเราต้องการทราบว่าเพศสัมพันธ์กับการเลือกพรรคการเมืองหรือไม่ เราสุ่มตัวอย่างผู้มีสิทธิเลือกตั้ง 500 คน และถามพวกเขาเกี่ยวกับความชอบพรรคการเมืองของพวกเขา ตารางต่อไปนี้แสดงผลการสำรวจ:
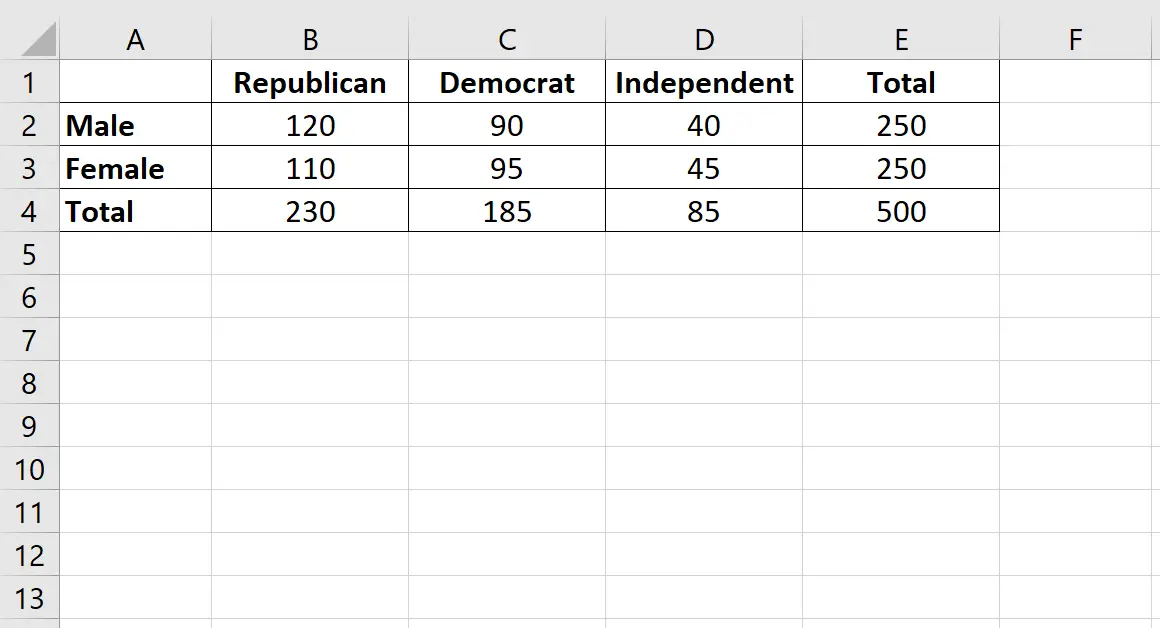
ใช้ขั้นตอนต่อไปนี้เพื่อทำการทดสอบไคสแควร์เพื่อตัดสินว่าเพศสัมพันธ์กับความชอบของพรรคการเมืองหรือไม่
ขั้นตอนที่ 1: กำหนดสมมติฐาน
เราจะทำการทดสอบความเป็นอิสระของไคสแควร์โดยใช้สมมติฐานต่อไปนี้:
- H 0 : การกำหนดเพศและพรรคการเมืองมีความเป็นอิสระ
- H 1 : เพศและความชอบของพรรคการเมือง ไม่ เป็นอิสระ
ขั้นตอนที่ 2: คำนวณค่าที่คาดหวัง
ต่อไปเราจะคำนวณค่าที่คาดหวังสำหรับแต่ละเซลล์ในตารางฉุกเฉินโดยใช้สูตรต่อไปนี้:
ค่าที่คาดหวัง = (ผลรวมของแถว * ผลรวมของคอลัมน์) / ผลรวมของตาราง
ตัวอย่างเช่น ค่าที่คาดหวังสำหรับผู้ชายพรรครีพับลิกันคือ: (230*250) / 500 = 115
เราสามารถทำซ้ำสูตรนี้เพื่อให้ได้ค่าที่คาดหวังสำหรับแต่ละเซลล์ของตาราง:
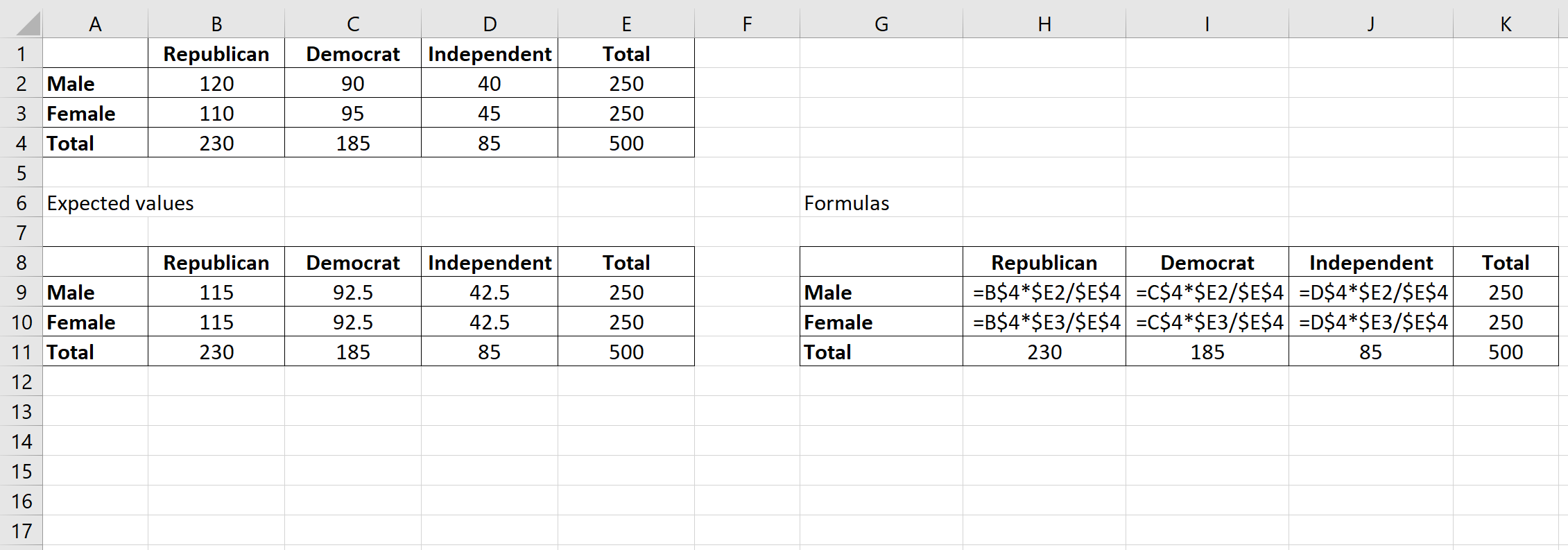
ขั้นตอนที่ 3: คำนวณ (OE) 2 /E สำหรับแต่ละเซลล์ในตาราง
ต่อไป เราจะคำนวณ (OE) 2 /E สำหรับแต่ละเซลล์ในตารางโดยที่:
- O: ค่าที่สังเกตได้
- E: ค่าที่คาดหวัง
ตัวอย่างเช่น ชายรีพับลิกันจะมีค่าเป็น: (120-115) 2 /115 = 0.2174
เราสามารถทำซ้ำสูตรนี้สำหรับแต่ละเซลล์ในตาราง:
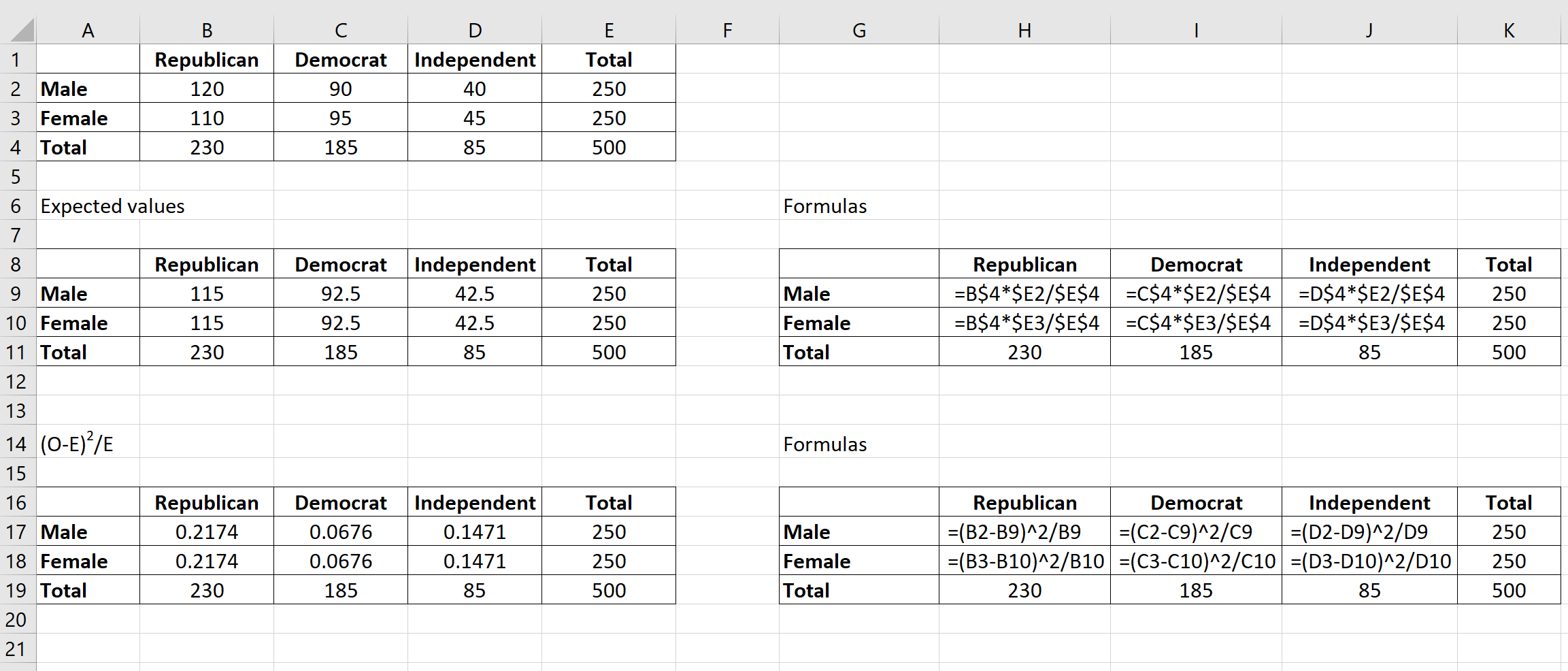
ขั้นตอนที่ 4: คำนวณสถิติการทดสอบ X2 และค่า p ที่สอดคล้องกัน
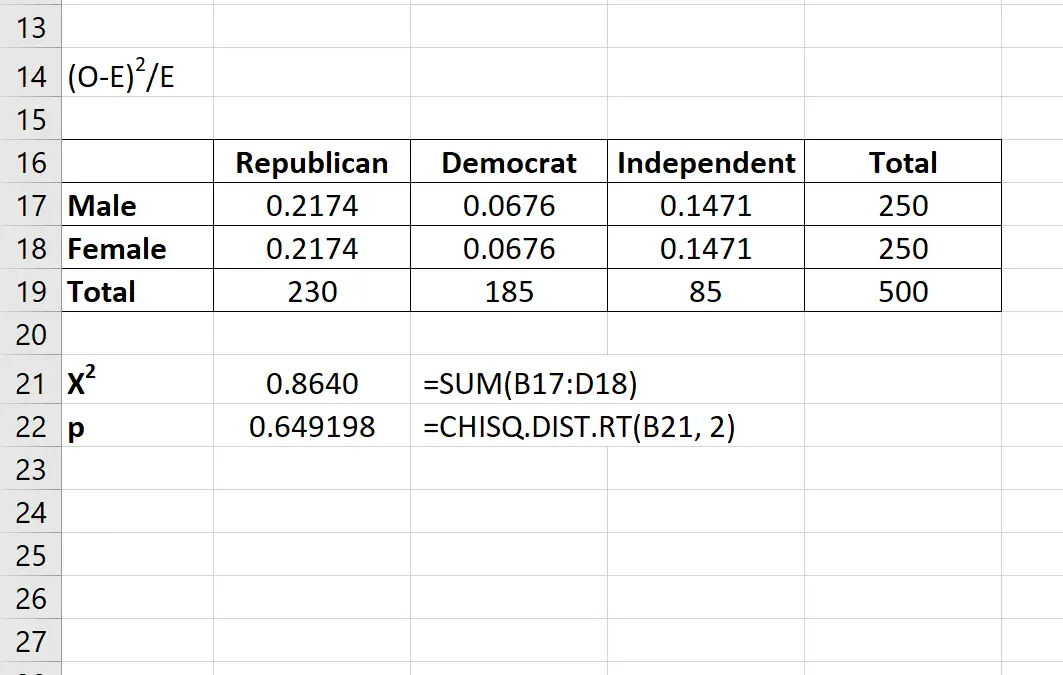
สถิติการทดสอบ X2 เป็นเพียงผลรวมของค่าในตารางสุดท้าย
ค่า p ที่สอดคล้องกับสถิติการทดสอบ X 2 สามารถพบได้โดยใช้สูตร:
=CHISQ.DIST.RT(x, deg_freedom)
ทอง:
- x: สถิติ การทดสอบ
- deg_freedom: องศาอิสระ คำนวณดังนี้: (#rows-1) * (#columns-1)
สถิติการทดสอบ X2 กลายเป็น 0.8640 และค่า p ที่สอดคล้องกันคือ 0.649198
ขั้นตอนที่ 5: วาดข้อสรุป
เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ ซึ่งหมายความว่าเราไม่มีหลักฐานเพียงพอที่จะกล่าวว่ามีความสัมพันธ์ระหว่างเพศและการตั้งค่าของพรรคการเมือง
หมายเหตุ: คุณยังสามารถทำการทดสอบทั้งหมดนี้ได้โดยใช้ เครื่องคำนวณการทดสอบอิสรภาพของ Chi-Square