วิธีใช้การทดสอบของ dunnett สำหรับการเปรียบเทียบหลายรายการ
การวิเคราะห์ความแปรปรวน (การวิเคราะห์ความแปรปรวน) ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่
หาก ค่า p ของ ANOVA ต่ำกว่าระดับนัยสำคัญที่เลือกไว้ เราสามารถปฏิเสธสมมติฐานว่างและสรุปได้ว่าเรามีหลักฐานเพียงพอที่จะบอกว่าค่าเฉลี่ยของกลุ่มอย่างน้อยหนึ่งรายการแตกต่างจากค่าเฉลี่ยอื่นๆ
อย่างไรก็ตาม นี่ไม่ได้บอกเราว่ากลุ่ม ใด มีความแตกต่างกัน นี่บอกเราว่าค่าเฉลี่ยกลุ่มไม่เท่ากันทั้งหมด หากต้องการทราบว่ากลุ่มใดมีความแตกต่างกัน เราจำเป็นต้องทำการ ทดสอบหลังการทดสอบ
หากกลุ่มใดกลุ่มหนึ่งในการศึกษาถือเป็น กลุ่มควบคุม เราก็ควรใช้ การทดสอบของ Dunnett เป็นการทดสอบหลังการวิเคราะห์ความแปรปรวน
การทดสอบ Dunnett: คำจำกัดความ
เราสามารถใช้สองขั้นตอนต่อไปนี้เพื่อทำการทดสอบ Dunnett:
ขั้นตอนที่ 1: ค้นหาค่าวิกฤตของ Dunnett
ก่อนอื่น เราต้องค้นหาคุณค่าวิกฤตของ Dunnett มีการคำนวณดังนี้:
ค่าวิกฤติ Dunnett: t d √ 2MS w /n
ทอง:
- t d : ค่าที่พบใน ตารางของ Dunnett สำหรับระดับอัลฟาที่กำหนด จำนวนกลุ่ม และขนาดตัวอย่างของกลุ่ม
- MS w : กำลังสองเฉลี่ยของ “ภายในกลุ่ม” ในตารางเอาต์พุต ANOVA
- n: ขนาดตัวอย่างกลุ่ม
ขั้นตอนที่ 2: เปรียบเทียบความแตกต่างระหว่างค่าเฉลี่ยกลุ่มกับค่าวิกฤตของ Dunnett
ต่อไป เราจะคำนวณความแตกต่างสัมบูรณ์ระหว่างค่าเฉลี่ยของแต่ละกลุ่มกับค่าเฉลี่ยของกลุ่มควบคุม หากความแตกต่างเกินค่าวิกฤตของ Dunnett ก็ถือว่าความแตกต่างนี้มีนัยสำคัญทางสถิติ
ตัวอย่างต่อไปนี้แสดงวิธีดำเนินการทดสอบ Dunnett ในทางปฏิบัติ
การทดสอบ Dunnett: ตัวอย่าง
สมมติว่าครูต้องการทราบว่าเทคนิคการเรียนรู้ใหม่สองเทคนิคมีศักยภาพในการปรับปรุงคะแนนสอบของนักเรียนหรือไม่ เพื่อทดสอบสิ่งนี้ เธอสุ่มแบ่งชั้นเรียนที่มีนักเรียน 30 คนออกเป็นสามกลุ่มดังต่อไปนี้:
- กลุ่มควบคุม: นักเรียน 10 คน
- นักเรียนศึกษาด้านเทคนิคใหม่ 1:10
- การศึกษาด้านเทคนิคใหม่ 2: 10 นักเรียน
หลังจากใช้เทคนิคการเรียนที่ได้รับมอบหมายมาหนึ่งสัปดาห์ นักเรียนแต่ละคนจะสอบแบบเดียวกัน ผลลัพธ์มีดังนี้:
- คะแนนสอบเฉลี่ยกลุ่มควบคุม : 81.6
- คะแนนสอบเฉลี่ยเทคนิคการเรียนใหม่ กลุ่ม 1 : 85.8
- คะแนนเฉลี่ยของการสอบกลุ่มเทคนิคการศึกษาใหม่ 2: 87.7
- กำลังสองเฉลี่ยของ “ภายในกลุ่ม” ในตารางเอาต์พุต ANOVA: 23.3
ด้วยข้อมูลนี้ เราจึงสามารถทำการทดสอบ Dunnett เพื่อตรวจสอบว่าหนึ่งในสองเทคนิคการศึกษาใหม่นี้สร้างคะแนนสอบเฉลี่ยที่แตกต่างกันอย่างมีนัยสำคัญมากกว่ากลุ่มควบคุมหรือไม่
ขั้นตอนที่ 1: ค้นหาค่าวิกฤตของ Dunnett
เมื่อใช้ α = 0.05 ขนาดกลุ่มตัวอย่าง n = 10 และผลรวมของกลุ่ม = 3 ตารางของ Dunnett บอกให้เราใช้ค่า 2.57 ในการคำนวณค่าวิกฤต
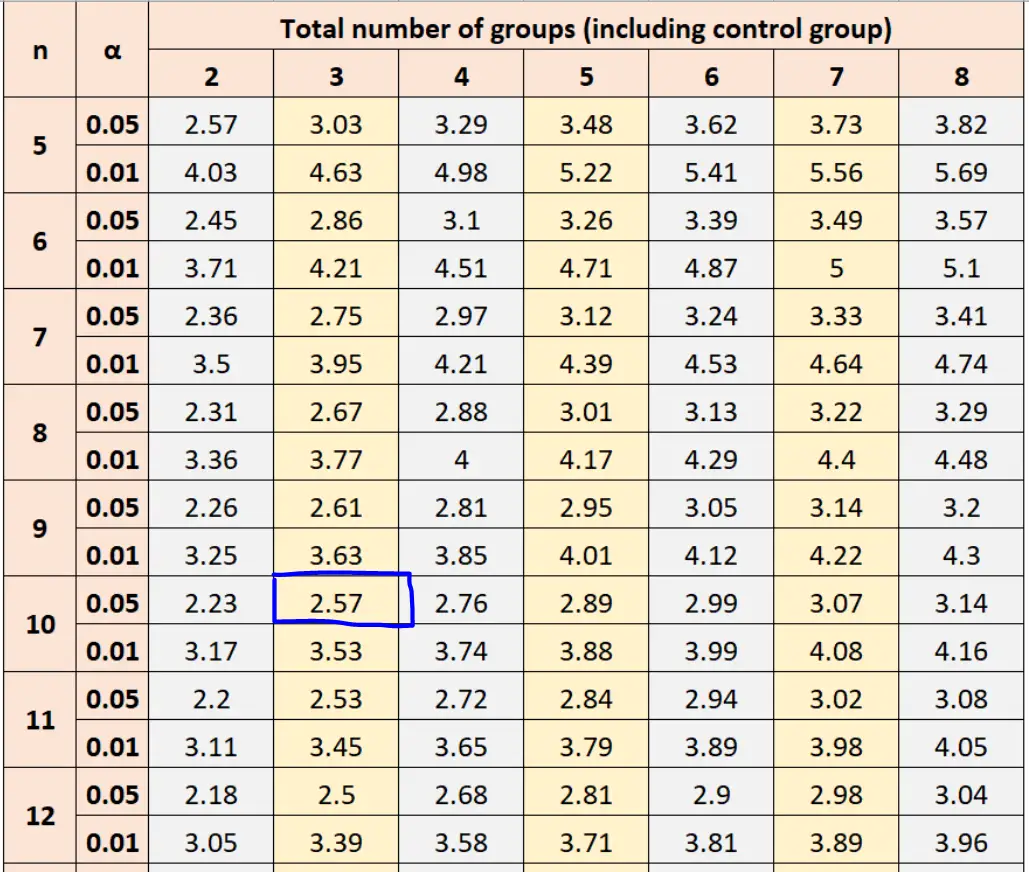
จากนั้นเราแทนค่าตัวเลขนี้ลงในสูตรเพื่อค้นหาค่า Dunnett วิกฤตได้:
ค่าวิกฤติของ Dunnett: t d √ 2MS w /n = 2.57√ 2(23.3)/10 = 5.548
ขั้นตอนที่ 2: เปรียบเทียบความแตกต่างระหว่างค่าเฉลี่ยกลุ่มกับค่าวิกฤตของ Dunnett
ความแตกต่างสัมบูรณ์ระหว่างวิธีการของแต่ละเทคนิคการศึกษากับกลุ่มควบคุมมีดังนี้:
- หน้าท้อง ความแตกต่างระหว่างเทคนิคใหม่ 1 และกลุ่มควบคุม: |85.8 – 81.6| = 4.2
- หน้าท้อง ความแตกต่างระหว่างเทคนิคใหม่ 2 และส่วนควบคุม: |87.7 – 81.6| = 6.1
เฉพาะความแตกต่างสัมบูรณ์ระหว่างเทคนิค 2 และกลุ่มควบคุมเท่านั้นที่มากกว่าค่าวิกฤติ Dunnett ที่ 5,548
ดังนั้น เราสามารถพูดได้ว่าเทคนิคการศึกษาใหม่ #2 ให้ผลการสอบที่แตกต่างกันอย่างมีนัยสำคัญเมื่อเทียบกับกลุ่มควบคุม แต่นี่ไม่ใช่กรณีของเทคนิคการศึกษาใหม่ #1
แหล่งข้อมูลเพิ่มเติม
ข้อมูลเบื้องต้นเกี่ยวกับการวิเคราะห์ความแปรปรวนแบบทางเดียว
คู่มือการใช้การทดสอบหลังการทดลองด้วย ANOVA
วิธีทำการทดสอบ Dunnett ใน R