วิธีทดสอบความเป็นปกติใน r (4 วิธี)

การทดสอบทางสถิติจำนวนมาก ถือว่า ชุดข้อมูลมีการกระจายตามปกติ

มีสี่วิธีทั่วไปในการตรวจสอบสมมติฐานนี้ใน R:

1. (วิธีการมองเห็น) สร้างฮิสโตแกรม

• ถ้าฮิสโตแกรมมีรูปร่างประมาณ “ระฆัง” จะถือว่าข้อมูลมีการกระจายตามปกติ

2. (วิธีการมองเห็น) สร้างพล็อต QQ

• หากจุดบนโครงเรื่องอยู่ตามแนวเส้นทแยงมุมโดยประมาณ ก็จะถือว่าข้อมูลมีการกระจายตามปกติ

3. (การทดสอบทางสถิติอย่างเป็นทางการ) ทำการทดสอบชาปิโร-วิลค์

• หากค่า p ของการทดสอบมากกว่า α = 0.05 จะถือว่าข้อมูลมีการกระจายตามปกติ

4. (การทดสอบทางสถิติอย่างเป็นทางการ) ทำการทดสอบ Kolmogorov-Smirnov

• หากค่า p ของการทดสอบมากกว่า α = 0.05 จะถือว่าข้อมูลมีการกระจายตามปกติ

ตัวอย่างต่อไปนี้แสดงวิธีการใช้แต่ละวิธีในทางปฏิบัติ

วิธีที่ 1: สร้างฮิสโตแกรม

รหัสต่อไปนี้แสดงวิธีการสร้างฮิสโตแกรมสำหรับชุดข้อมูลแบบกระจายแบบปกติและแบบไม่กระจายแบบปกติใน R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

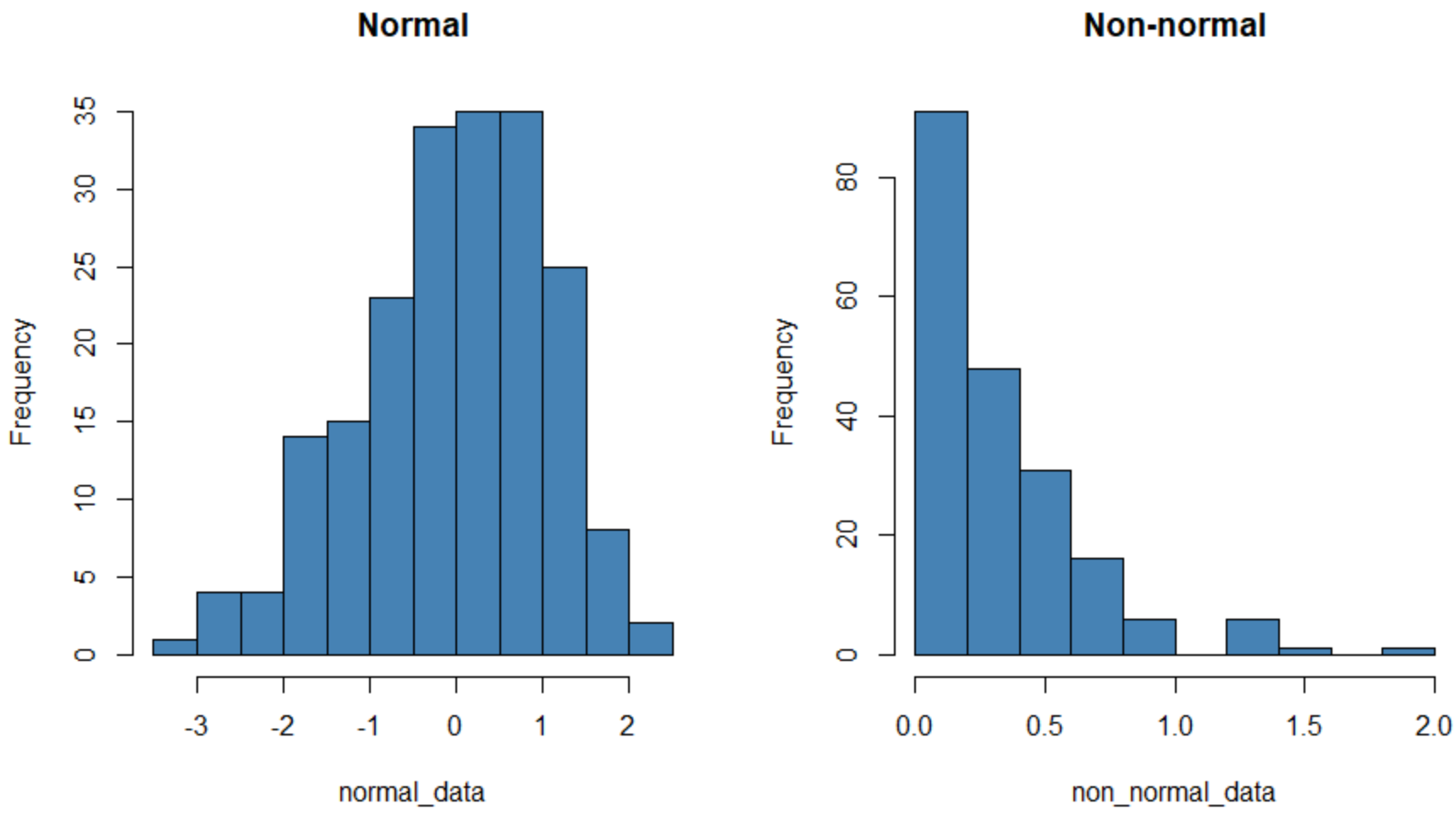
ฮิสโตแกรมทางด้านซ้ายแสดงชุดข้อมูลที่แจกแจงตามปกติ (มีรูปร่างคล้ายระฆัง) และฮิสโตแกรมทางขวาแสดงชุดข้อมูลที่ไม่มีการแจกแจงตามปกติ

วิธีที่ 2: สร้างพล็อต QQ

รหัสต่อไปนี้แสดงวิธีการสร้างพล็อต QQ สำหรับชุดข้อมูลแบบกระจายแบบปกติและแบบไม่กระจายแบบปกติใน R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

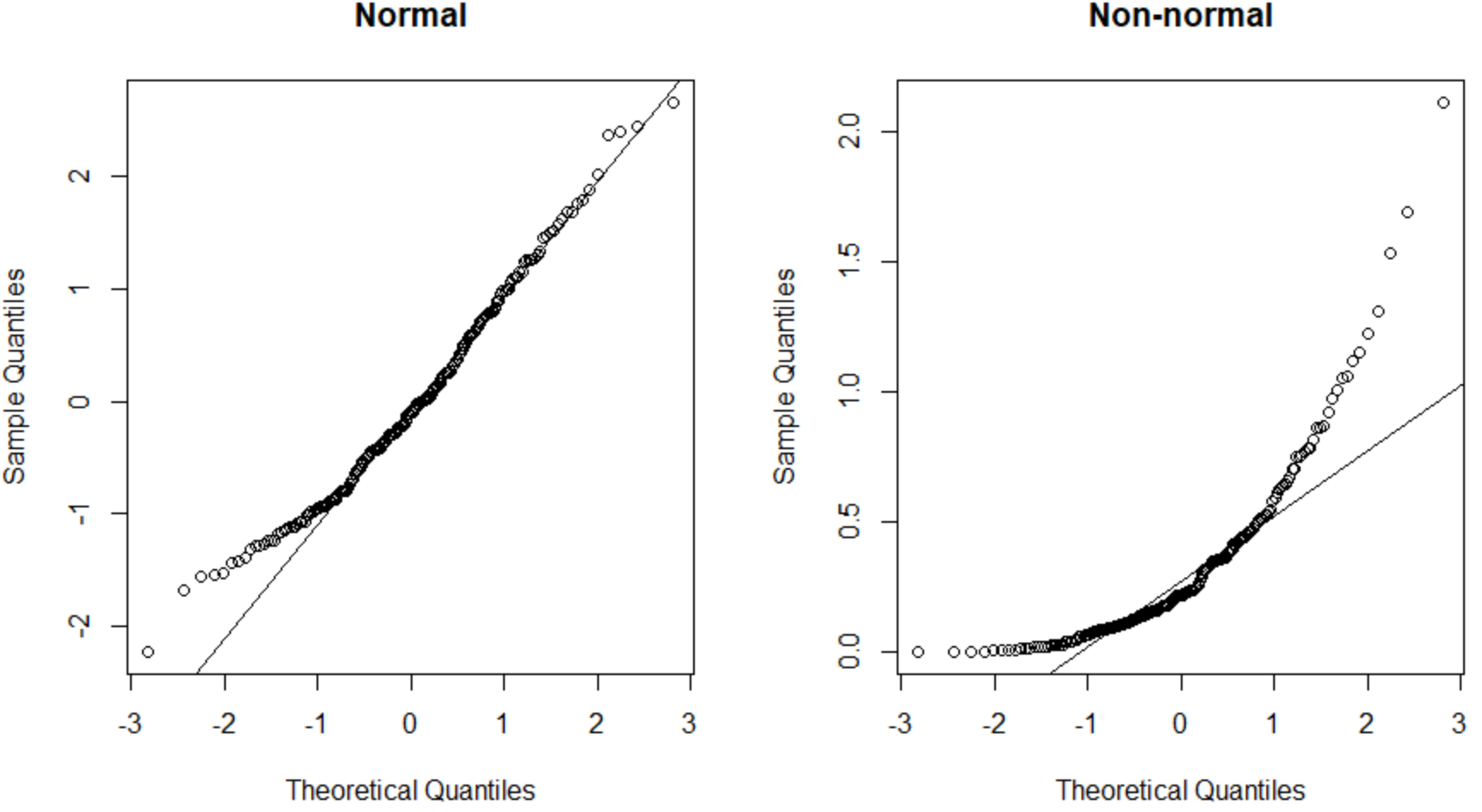
แผนภาพ QQ ทางด้านซ้ายแสดงชุดข้อมูลที่แจกแจงตามปกติ (จุดตกตามเส้นทแยงมุม) และแผนภาพ QQ ทางด้านขวาแสดงชุดข้อมูลที่ไม่ได้แจกแจงตามปกติ

วิธีที่ 3: ทำการทดสอบ Shapiro-Wilk

รหัสต่อไปนี้แสดงวิธีดำเนินการทดสอบ Shapiro-Wilk บนชุดข้อมูลแบบกระจายแบบปกติและแบบไม่กระจายแบบปกติใน R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

ค่า p ของการทดสอบครั้งแรกไม่น้อยกว่า 0.05 ซึ่งบ่งชี้ว่าข้อมูลมีการกระจายตามปกติ

ค่า p ของการทดสอบครั้งที่สอง น้อย กว่า 0.05 แสดงว่าข้อมูลไม่มีการกระจายตามปกติ

วิธีที่ 4: ทำการทดสอบ Kolmogorov-Smirnov

รหัสต่อไปนี้แสดงวิธีดำเนินการทดสอบ Kolmogorov-Smirnov บนชุดข้อมูลแบบกระจายแบบปกติและแบบไม่กระจายแบบปกติใน R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

ค่า p ของการทดสอบครั้งแรกไม่น้อยกว่า 0.05 ซึ่งบ่งชี้ว่าข้อมูลมีการกระจายตามปกติ

ค่า p ของการทดสอบครั้งที่สอง น้อย กว่า 0.05 แสดงว่าข้อมูลไม่มีการกระจายตามปกติ

วิธีจัดการกับข้อมูลที่ไม่ปกติ

หากชุดข้อมูลที่ระบุ ไม่ได้ รับการเผยแพร่ตามปกติ เรามักจะสามารถดำเนินการแปลงอย่างใดอย่างหนึ่งต่อไปนี้เพื่อให้มีการกระจายแบบปกติมากขึ้น:

1. การแปลงบันทึก: แปลงค่า x เป็น log(x)

2. การแปลงรากที่สอง: แปลงค่าของ x เป็น √x

3. การแปลงรูทคิวบ์: แปลงค่าของ x เป็น x ^1/3 .

เมื่อทำการแปลงเหล่านี้ ชุดข้อมูลจะมีการกระจายตามปกติมากขึ้น

อ่าน บทช่วยสอนนี้ เพื่อดูวิธีดำเนินการแปลงเหล่านี้ใน R

แหล่งข้อมูลเพิ่มเติม

วิธีสร้างฮิสโตแกรมใน R
วิธีสร้างและตีความพล็อต QQ ใน R
วิธีทำการทดสอบ Shapiro-Wilk ใน R
วิธีทำการทดสอบ Kolmogorov-Smirnov ใน R