การทดสอบสมมุติฐานเพื่อหาค่าเฉลี่ย
บทความนี้จะอธิบายว่าการทดสอบสมมติฐานสำหรับค่าเฉลี่ยคืออะไรในสถิติ ดังนั้นคุณจะพบสูตรทดสอบสมมติฐานสำหรับค่าเฉลี่ยและแบบฝึกหัดที่แก้ไขทีละขั้นตอน
การทดสอบสมมติฐานสำหรับค่าเฉลี่ยคืออะไร?
การทดสอบสมมติฐานเพื่อหาค่าเฉลี่ย เป็นวิธีการทางสถิติที่ใช้ในการปฏิเสธหรือปฏิเสธสมมติฐานว่างของค่าเฉลี่ยประชากร
โดยเฉพาะอย่างยิ่ง การทดสอบสมมติฐานสำหรับค่าเฉลี่ยเกี่ยวข้องกับการคำนวณสถิติการทดสอบแล้วเปรียบเทียบกับค่าวิกฤตเพื่อปฏิเสธสมมติฐานว่างหรือไม่
ควรสังเกตว่าการทดสอบสมมติฐานมีชื่อต่างกัน ในสถิติ เรียกอีกอย่างว่าข้อแตกต่างของสมมติฐาน การทดสอบสมมติฐาน หรือการทดสอบนัยสำคัญ
สูตรทดสอบสมมุติฐานสำหรับค่าเฉลี่ย
ต่อไปเราจะดูว่าสถิติการทดสอบสมมติฐานสำหรับค่าเฉลี่ยคำนวณอย่างไร อย่างไรก็ตาม สูตรจะแตกต่างกันเล็กน้อยขึ้นอยู่กับว่าทราบความแปรปรวนหรือไม่ ดังนั้นก่อนอื่นเราจะมาดูกันก่อนว่าจะดำเนินการอย่างไรเมื่อทราบความแปรปรวน และเมื่อไม่ทราบความแปรปรวน
ด้วยความเบี่ยงเบนที่รู้จัก
สูตรสมมติฐานการทดสอบสำหรับค่าเฉลี่ยที่มีความแปรปรวนที่ทราบ คือ:

ทอง:
-

คือสถิติการทดสอบสมมติฐานของค่าเฉลี่ย
-

คือค่าเฉลี่ยตัวอย่าง
-

คือค่าเฉลี่ยที่เสนอ
-

คือค่าเบี่ยงเบนมาตรฐานประชากร
-

คือขนาดตัวอย่าง
เมื่อคำนวณสถิติการทดสอบสมมติฐานสำหรับค่าเฉลี่ยแล้ว ควรตีความผลลัพธ์เพื่อปฏิเสธหรือปฏิเสธสมมติฐานว่าง:
- หากการทดสอบสมมติฐานสำหรับค่าเฉลี่ยเป็นแบบสองด้าน สมมติฐานว่างจะถูกปฏิเสธหากค่าสัมบูรณ์ของสถิติมากกว่าค่าวิกฤต Z α/2
- หากการทดสอบสมมติฐานสำหรับค่าเฉลี่ยตรงกับหางด้านขวา สมมติฐานว่างจะถูกปฏิเสธหากสถิติมากกว่าค่าวิกฤต Z α
- หากการทดสอบสมมติฐานสำหรับค่าเฉลี่ยตรงกับหางซ้าย สมมติฐานว่างจะถูกปฏิเสธหากสถิติน้อยกว่าค่าวิกฤต -Z α
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0e2ccadfc369eb7543b8f86dfccc528e_l3.png)
ในกรณีนี้ ค่าวิกฤตจะได้มาจาก ตารางการแจกแจงแบบปกติที่เป็นมาตรฐาน
โดยไม่ทราบความแปรปรวน
สูตรสมมติฐานการทดสอบสำหรับค่าเฉลี่ยที่ไม่ทราบความแปรปรวน คือ:

ทอง:
-

คือสถิติการทดสอบสมมติฐานสำหรับค่าเฉลี่ย ซึ่งกำหนดโดย การแจกแจงแบบ t ของนักเรียน
-

คือค่าเฉลี่ยตัวอย่าง
-

คือค่าเฉลี่ยที่เสนอ
-

คือค่าเบี่ยงเบนมาตรฐานตัวอย่าง
-

คือขนาดตัวอย่าง
เช่นเคย ผลการคำนวณของสถิติการทดสอบจะต้องตีความด้วยค่าวิกฤตเพื่อปฏิเสธหรือไม่ใช้สมมติฐานว่าง:
- หากการทดสอบสมมติฐานสำหรับค่าเฉลี่ยเป็นแบบสองด้าน สมมติฐานว่างจะถูกปฏิเสธหากค่าสัมบูรณ์ของสถิติมากกว่าค่าวิกฤต t α/2|n-1
- หากการทดสอบสมมติฐานสำหรับค่าเฉลี่ยตรงกับหางด้านขวา สมมติฐานว่างจะถูกปฏิเสธหากสถิติมากกว่าค่าวิกฤต t α|n-1
- หากการทดสอบสมมติฐานสำหรับค่าเฉลี่ยตรงกับหางซ้าย สมมติฐานว่างจะถูกปฏิเสธหากสถิติน้อยกว่าค่าวิกฤต -t α|n-1
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-31fb206b75a47181c7c673f54ba28ee8_l3.png)
เมื่อไม่ทราบความแปรปรวน ค่าทดสอบวิกฤตจะได้มาจากตารางการแจกแจงของนักเรียน
ตัวอย่างการทดสอบสมมติฐานสำหรับค่าเฉลี่ยในโลกแห่งความเป็นจริง
เพื่อให้เข้าใจแนวคิดของการทดสอบสมมติฐานสำหรับค่าเฉลี่ยประชากรอย่างถ่องแท้ คุณสามารถดูตัวอย่างในชีวิตจริงของการทดสอบสมมติฐานประเภทนี้ได้ที่ด้านล่าง
- บริษัทเทคโนโลยีอ้างว่าแบตเตอรี่ของแล็ปท็อปที่จำหน่ายใช้งานได้ 6 ชั่วโมง เราตรวจสอบว่าสมมติฐานนี้เป็นเท็จหรือไม่โดยทำการทดสอบสมมติฐานด้วยระดับนัยสำคัญ α = 0.05 ในการดำเนินการนี้จึงตัดสินใจซื้อ 20 เครื่องและสังเกตอายุการใช้งานแบตเตอรี่ของคอมพิวเตอร์แต่ละเครื่อง (ค่าแสดงเป็นชั่วโมง):
5.2 5.9 7.1 4.2 6.5
8.5 4.6 6.8 6.9 5.8
5.1 6.5 7.0 5.3 6.2
5.7 6.6 7.5 5.1 6.1
ในกรณีนี้ สมมติฐานว่างและทางเลือก ของการทดสอบสมมติฐานเกี่ยวกับค่าเฉลี่ยมีดังนี้:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-329ffe392783b8bee1eef642d1a45f53_l3.png)
เพื่อระบุสถิติการทดสอบ เราต้องคำนวณค่าเฉลี่ยตัวอย่างและค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างก่อน:
![]()
เนื่องจากเราไม่ทราบความแปรปรวนของประชากร เพื่อให้ได้สถิติการทดสอบ เราจึงจำเป็นต้องใช้สูตรการทดสอบสมมติฐานสำหรับค่าเฉลี่ยที่ไม่ทราบค่าความแปรปรวน:

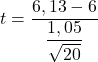
![]()
ตอนนี้เราจำเป็นต้องค้นหาค่าวิกฤตของการทดสอบสมมติฐาน ดังนั้นเราจึงดูค่าที่สอดคล้องกันใน ตารางการแจกแจง t ของนักเรียน องศาอิสระของนักเรียนมีค่าน้อยกว่าขนาดกลุ่มตัวอย่างหนึ่ง (20-1=19) และในทางกลับกัน ความน่าจะเป็นที่สอดคล้องกันคือครึ่งหนึ่งของระดับนัยสำคัญ (0.05/2= 0.025) เนื่องจากเป็นแบบสองด้าน การทดสอบสมมติฐาน.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e85692dfb2fb2522025566dc205b8117_l3.png)
โดยสรุป เนื่องจากนี่คือการทดสอบสมมติฐานแบบสองด้านและค่าสัมบูรณ์ของสถิติการทดสอบน้อยกว่าค่าวิกฤต สมมติฐานว่างจะไม่ถูกปฏิเสธ แต่สมมติฐานทางเลือกจะถูกปฏิเสธ
![]()
การทดสอบสมมติฐานเพื่อหาความแตกต่างในค่าเฉลี่ย
ความแตกต่างในการทดสอบสมมติฐานเฉลี่ย ใช้เพื่อปฏิเสธหรือยอมรับสมมติฐานว่างที่ว่าค่าเฉลี่ยของประชากรทั้งสองมีค่าเท่ากัน
ดังนั้นสมมติฐานว่างของการทดสอบสมมติฐานสำหรับผลต่างของสองค่าเฉลี่ยจะเป็นดังนี้เสมอ:
![]()
ในขณะที่สมมติฐานทางเลือกสามารถเป็นหนึ่งในสามข้อต่อไปนี้:
![Rendered by QuickLaTeX.com \begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c612ac7651faad9faa195f37fdf6edef_l3.png)
จากนั้น สูตรในการคำนวณสถิติการทดสอบสมมติฐานสำหรับความแตกต่างในค่าเฉลี่ยเมื่อทราบความแปรปรวน คือ:
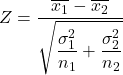
ทอง:
-

คือสถิติการทดสอบสมมติฐานสำหรับผลต่างของสองค่าเฉลี่ยที่มีความแปรปรวนที่ทราบ ซึ่งเป็นไปตามการแจกแจงแบบปกติมาตรฐาน
-

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 1
-

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 2
-

คือความแปรปรวนของประชากร 1
-

คือความแปรปรวนของประชากร 2
-

คือขนาดตัวอย่างที่ 1
-

คือขนาดตัวอย่างที่ 2
ในทางกลับกัน สูตรคำนวณสถิติการทดสอบสมมติฐานสำหรับความแตกต่างในค่าเฉลี่ยเมื่อไม่ทราบความแปรปรวน มีดังนี้
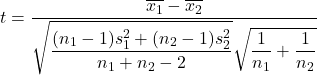
ทอง:
-

คือสถิติการทดสอบสมมติฐานสำหรับผลต่างของสองค่าเฉลี่ยโดยไม่ทราบความแปรปรวน ซึ่งเป็นไปตามการแจกแจงแบบ t ของนักเรียน
-

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 1
-

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 2
-

คือความแปรปรวนของกลุ่มตัวอย่างที่ 1
-

คือความแปรปรวนของกลุ่มตัวอย่าง 2
-

คือขนาดตัวอย่างที่ 1
-

คือขนาดตัวอย่างที่ 2