การทดสอบสมมติฐานเพื่อหาความแตกต่างในค่าเฉลี่ย
บทความนี้จะอธิบายว่าค่าเฉลี่ยของการทดสอบสมมติฐานในสถิติแตกต่างกันอย่างไร และใช้เพื่ออะไร ในทำนองเดียวกัน คุณจะค้นพบวิธีทดสอบสมมติฐานเกี่ยวกับความแตกต่างในวิธีการและแบบฝึกหัดที่มีการแก้ไขทีละขั้นตอน
การทดสอบสมมติฐานเพื่อหาผลต่างเฉลี่ยคืออะไร
การทดสอบสมมติฐานสำหรับความแตกต่างในค่าเฉลี่ย คือการทดสอบทางสถิติที่ใช้ในการปฏิเสธหรือยอมรับสมมติฐานที่ว่าค่าเฉลี่ยของประชากรทั้งสองแตกต่างกัน นั่นคือใช้ความแตกต่างในการทดสอบสมมติฐานเพื่อพิจารณาว่าค่าเฉลี่ยของประชากรทั้งสองเหมือนกันหรือต่างกัน
โปรดทราบว่าการตัดสินใจในการทดสอบสมมติฐานนั้นขึ้นอยู่กับ ระดับความเชื่อมั่น ที่กำหนดไว้ก่อนหน้านี้ ดังนั้นจึงไม่สามารถรับประกันได้ว่าผลลัพธ์ของการทดสอบสมมติฐานนั้นถูกต้องเสมอไป แต่จะเป็นผลลัพธ์ที่เป็นไปได้มากที่สุดว่าเป็นจริง
การทดสอบสมมติฐานสำหรับผลต่างของทั้งสองวิธีเกี่ยวข้องกับการคำนวณสถิติการทดสอบและเปรียบเทียบกับค่าวิกฤตเพื่อปฏิเสธสมมติฐานว่างหรือไม่ ด้านล่างนี้เราจะดูวิธีทดสอบสมมติฐานเพื่อหาค่ากลางที่แตกต่างกัน
สุดท้ายนี้ โปรดจำไว้ว่าในสถิติ การทดสอบสมมติฐานอาจเรียกอีกอย่างว่าความแตกต่างของสมมติฐาน การทดสอบสมมติฐาน หรือการทดสอบนัยสำคัญ
สูตรทดสอบสมมติฐานสำหรับความแตกต่างในค่าเฉลี่ย
สูตรที่ควรใช้ในการทดสอบสมมติฐานเกี่ยวกับความแตกต่างในค่าเฉลี่ยจะแตกต่างกันไปขึ้นอยู่กับว่าทราบความแปรปรวนของประชากรหรือไม่ และหากไม่ทราบ ก็ถือว่าค่าดังกล่าวเหมือนหรือต่างกันได้หรือไม่ ดังนั้นในส่วนนี้เราจะมาดูกันว่าจะใช้สูตรไหนแล้วแต่กรณี
รูปแบบที่รู้จัก
สูตรคำนวณสถิติการทดสอบสมมติฐานสำหรับผลต่างของค่าเฉลี่ยเมื่อทราบความแปรปรวน มีดังนี้

ทอง:
-

คือสถิติการทดสอบสมมติฐานสำหรับผลต่างของสองค่าเฉลี่ยที่มีความแปรปรวนที่ทราบ ซึ่งเป็นไปตามการแจกแจงแบบปกติมาตรฐาน
-

คือค่าเฉลี่ยของประชากร 1
-

คือค่าเฉลี่ยของประชากร 2
-

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 1
-

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 2
-

คือค่าเบี่ยงเบนมาตรฐานของประชากร 1
-

คือค่าเบี่ยงเบนมาตรฐานของประชากร 2
-

คือขนาดตัวอย่างที่ 1
-

คือขนาดตัวอย่างที่ 2
โปรดทราบว่านี่เป็นกรณีทั่วไปน้อยที่สุด ดังนั้นสูตรนี้จึงใช้เฉพาะในบางกรณีเท่านั้น
การเบี่ยงเบนที่ไม่รู้จักและเท่ากัน
สูตรในการคำนวณสถิติการทดสอบสมมติฐานสำหรับความแตกต่างในค่าเฉลี่ยเมื่อไม่ทราบความแปรปรวนของประชากรแต่ถือว่าเท่ากัน คือ

ทอง:
-

เป็นสถิติการทดสอบสมมติฐานสำหรับผลต่างในค่าเฉลี่ยโดยไม่ทราบความแปรปรวน ซึ่งเป็นไปตามการแจกแจงค่า t ของนักเรียนที่มีดีกรีอิสระ n 1 + n 2 -2
-

คือค่าเฉลี่ยของประชากร 1
-

คือค่าเฉลี่ยของประชากร 2
-

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 1
-

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 2
-

คือค่าเบี่ยงเบนมาตรฐานรวม
-

คือขนาดตัวอย่างที่ 1
-

คือขนาดตัวอย่างที่ 2
ค่าเบี่ยงเบนมาตรฐานรวมของทั้งสองตัวอย่างคำนวณโดยใช้สูตรต่อไปนี้:

รูปแบบที่ไม่รู้จักและแตกต่างกัน
เมื่อไม่ทราบความแปรปรวนของประชากรและถือว่าแตกต่างกัน สูตรในการคำนวณสถิติการทดสอบสมมติฐานสำหรับผลต่างของค่าเฉลี่ย มีดังนี้

ทอง:
-

เป็นสถิติการทดสอบสมมติฐานสำหรับผลต่างในค่าเฉลี่ยโดยไม่ทราบความแปรปรวน ซึ่งเป็นไปตามการแจกแจงแบบ t ของนักเรียน
-

คือค่าเฉลี่ยของประชากร 1
-

คือค่าเฉลี่ยของประชากร 2
-

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 1
-

คือค่าเฉลี่ยของกลุ่มตัวอย่างที่ 2
-

คือค่าเบี่ยงเบนมาตรฐานของประชากร 1
-

คือค่าเบี่ยงเบนมาตรฐานของประชากร 2
-

คือขนาดตัวอย่างที่ 1
-

คือขนาดตัวอย่างที่ 2
อย่างไรก็ตาม ในกรณีนี้ องศาอิสระของการแจกแจง t ของนักเรียนคำนวณโดยใช้สูตรต่อไปนี้:

ตัวอย่างการทดสอบสมมติฐานที่เป็นรูปธรรมสำหรับความแตกต่างในค่าเฉลี่ย
เพื่อให้การดูดซึมแนวคิดของการทดสอบสมมติฐานเกี่ยวกับความแตกต่างในค่าเฉลี่ยเสร็จสิ้น เราจะเห็นตัวอย่างที่เป็นรูปธรรมของการทดสอบสมมติฐานประเภทนี้
- คุณต้องการศึกษาทางสถิติเกี่ยวกับเงินเดือนของบริษัทคู่แข่งสองแห่ง โดยเฉพาะอย่างยิ่ง คุณต้องการพิจารณาว่าเงินเดือนโดยเฉลี่ยของทั้งสองบริษัทแตกต่างกันหรือไม่ ในการดำเนินการนี้ เราจะสุ่มตัวอย่างพนักงาน 47 คนจากบริษัทหนึ่งและอีกตัวอย่าง 55 คนจากอีกบริษัทหนึ่ง ตัวอย่างแรกจะได้เงินเดือนเฉลี่ย 40,000 ดอลลาร์และค่าเบี่ยงเบนมาตรฐาน 12,000 ดอลลาร์ ขณะที่ตัวอย่างที่สองจะได้เงินเดือนเฉลี่ย 46,000 ดอลลาร์และค่าเบี่ยงเบนมาตรฐาน 18,000 ดอลลาร์ ทำการทดสอบสมมติฐานด้วยระดับนัยสำคัญ 5% เพื่อพิจารณาว่าเงินเดือนโดยเฉลี่ยแตกต่างกันหรือไม่
ในกรณีนี้ สมมติฐานว่างและสมมติฐานทางเลือก ของการทดสอบสมมติฐานสำหรับผลต่างของทั้งสองวิธีมีดังนี้:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4dd9e80c0a87987d689d7b8d99be9d90_l3.png)
ในกรณีนี้ ไม่ทราบช่องว่างของประชากร แต่สามารถสันนิษฐานได้ว่ามีความเท่าเทียมกันเนื่องจากเป็นบริษัทคู่แข่ง และสภาพการทำงานของตลาดที่พวกเขาดำเนินธุรกิจมีความคล้ายคลึงกันมาก ดังนั้นสูตรสถิติการทดสอบสมมติฐานผลต่างของค่าเฉลี่ยที่เราควรใช้คือ

ดังนั้นเราจึงคำนวณค่าเบี่ยงเบนมาตรฐานรวมของกลุ่มตัวอย่างทั้งสอง:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0308363d68c4677761d44b214b1609d9_l3.png)
ตอนนี้เราใช้สูตรการทดสอบสมมติฐานสำหรับความแตกต่างในค่าเฉลี่ย:
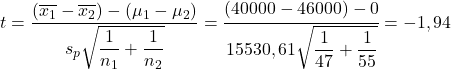
ในทางกลับกัน เรามองหาค่าวิกฤตของการทดสอบสมมติฐานสำหรับความแตกต่างในค่าเฉลี่ยใน ตาราง Student’s :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d5f11ecd0336e50c63b0ab2fab4bd530_l3.png)
จากนั้น เนื่องจากค่าสัมบูรณ์ของสถิติการทดสอบน้อยกว่าค่าการทดสอบวิกฤต จึงยอมรับสมมติฐานว่างและสมมติฐานทางเลือกจะถูกปฏิเสธ
![]()