การทดสอบอาหารคืออะไร? (คำอธิบายและตัวอย่าง)
การทดสอบ Chow คือการทดสอบทางสถิติที่พัฒนาโดย Gregory Chow นักเศรษฐศาสตร์ ซึ่งใช้เพื่อทดสอบว่าค่าสัมประสิทธิ์ของแบบจำลองการถดถอยที่ต่างกันสองตัวในชุดข้อมูลที่ต่างกันเท่ากันหรือไม่
โดยทั่วไปการทดสอบ Chow จะใช้ในด้านเศรษฐมิติพร้อมข้อมูลอนุกรมเวลาเพื่อพิจารณาว่าข้อมูลมีการแบ่งแยกทางโครงสร้าง ณ จุดใดเวลาหนึ่งหรือไม่
ตัวอย่างเช่น พิจารณาแผนภาพกระจายต่อไปนี้:
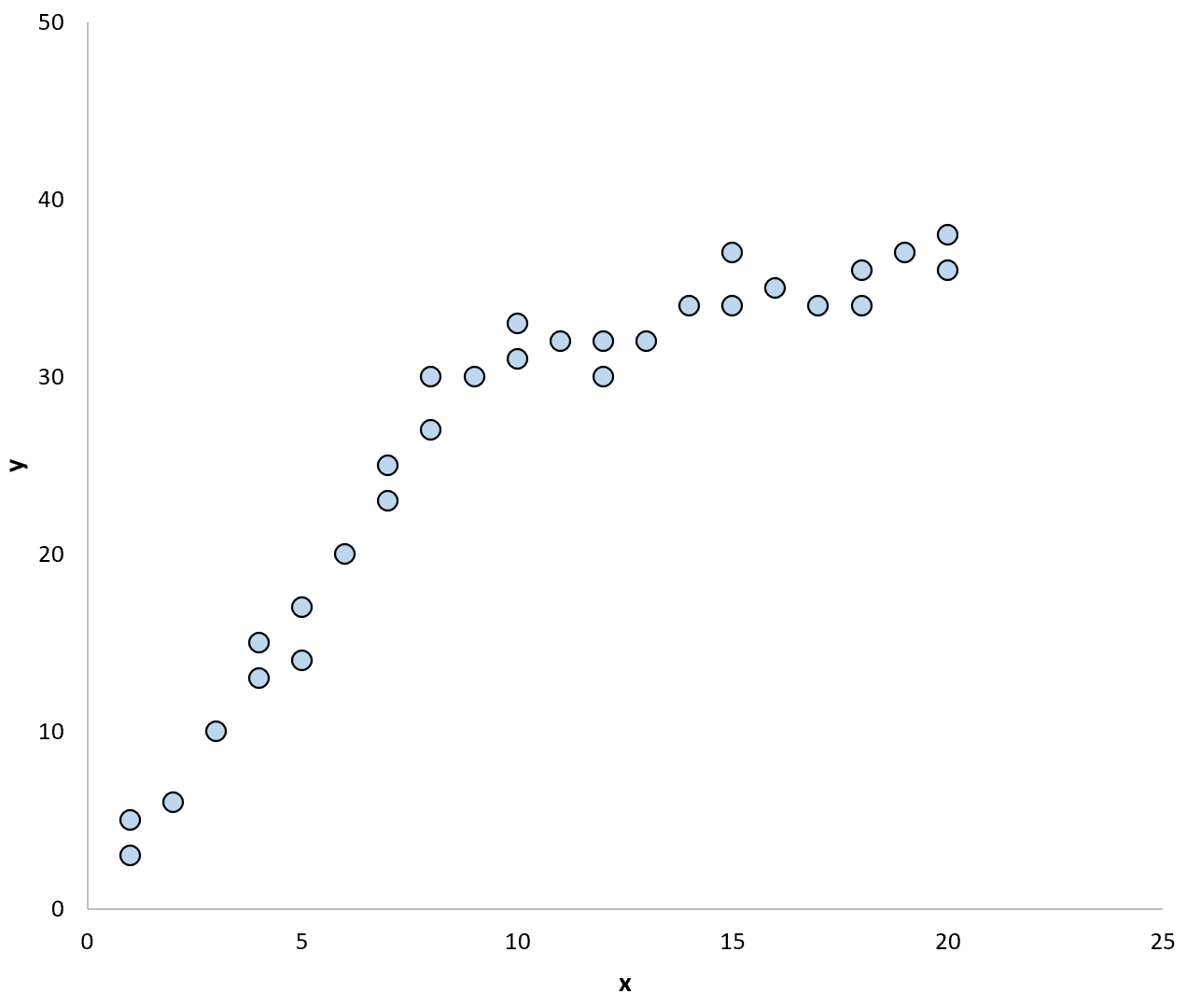
หากเราใช้เส้นการถดถอยเพื่อสรุปแบบจำลองในข้อมูล อาจมีลักษณะดังนี้:
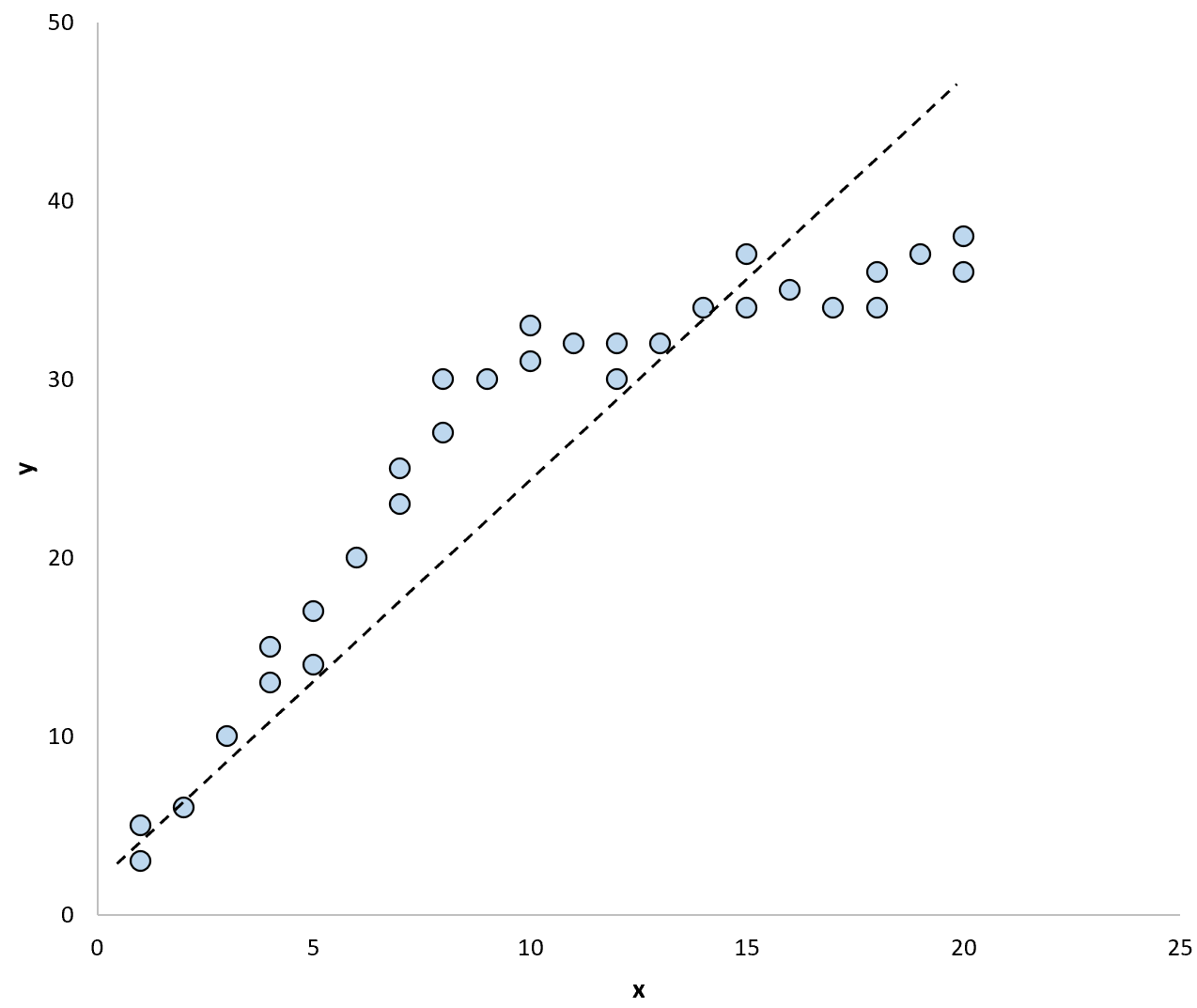
และหากเราใช้เส้นการถดถอยสองเส้นแยกกันเพื่อสรุปแบบจำลองในข้อมูล อาจมีลักษณะดังนี้:
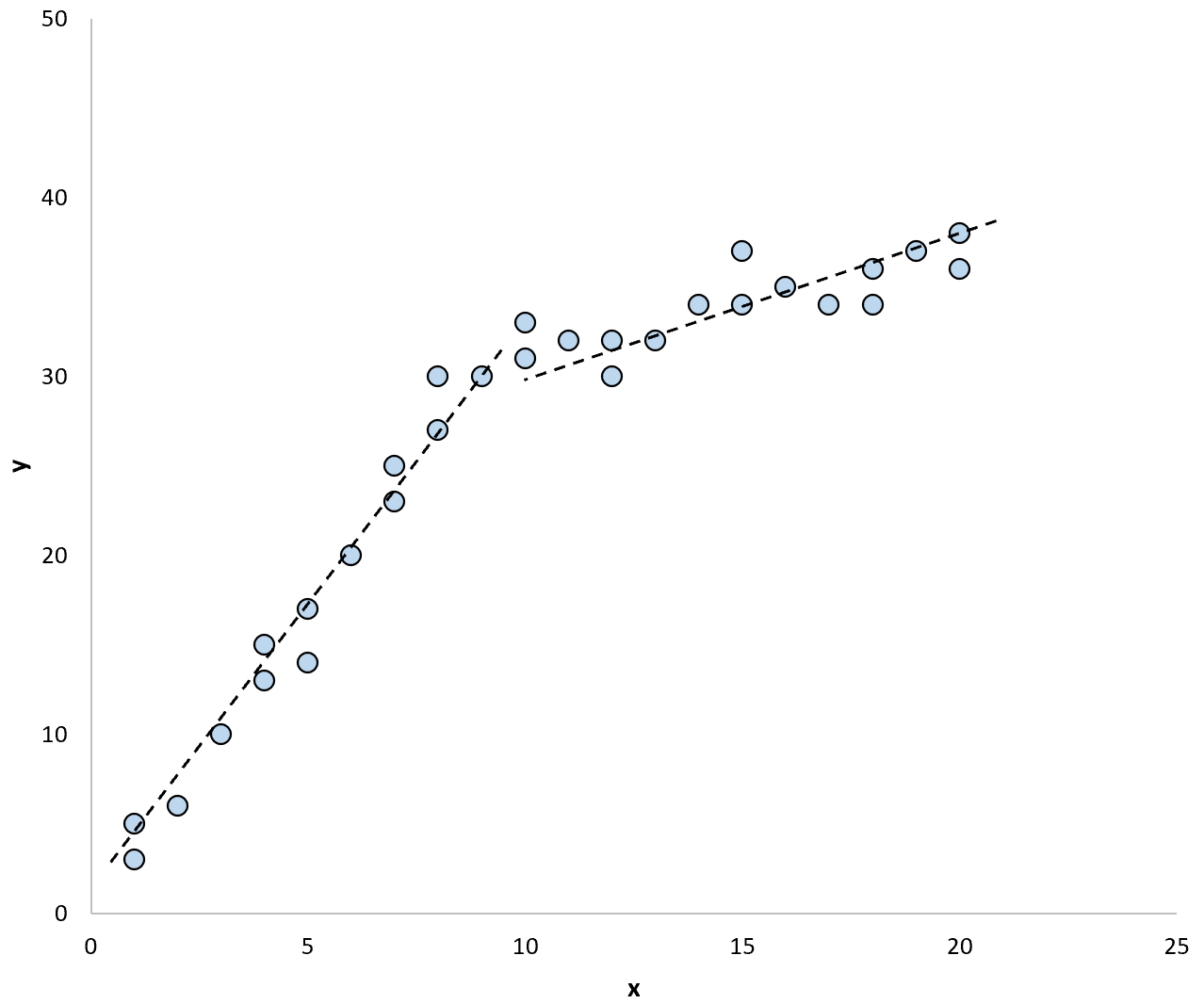
การทดสอบ Chow ช่วยให้เราสามารถทดสอบว่าค่าสัมประสิทธิ์การถดถอยของแต่ละเส้นการถดถอยเท่ากันหรือไม่
หากการทดสอบพบว่าค่าสัมประสิทธิ์ไม่เท่ากันระหว่างเส้นการถดถอย นั่นหมายความว่ามีหลักฐานสำคัญที่แสดงว่าข้อมูลมีการแตกแยกทางโครงสร้าง กล่าวอีกนัยหนึ่ง แนวโน้มข้อมูลจะแตกต่างกันมากก่อนและหลังจุดพักโครงสร้างนี้
เมื่อใดควรใช้การทดสอบ Chow
ตัวอย่างต่อไปนี้แสดงให้เห็นถึงสถานการณ์ที่คุณอาจต้องการทำการทดสอบ Chow:
1. พิจารณาว่าราคาหุ้นเคลื่อนไหวในอัตราที่แตกต่างกันก่อนและหลังการเลือกตั้งหรือไม่
2. พิจารณาว่าราคาบ้านเปลี่ยนแปลงก่อนและหลังการเปลี่ยนแปลงอัตราดอกเบี้ยหรือไม่
3. พิจารณาว่ากำไรเฉลี่ยของรัฐวิสาหกิจแตกต่างกันก่อนและหลังการนำกฎหมายภาษีฉบับใหม่มาใช้หรือไม่
ในแต่ละสถานการณ์ เราสามารถใช้การทดสอบ Chow เพื่อพิจารณาว่ามีจุดพักเชิงโครงสร้างในข้อมูลในช่วงเวลาใดก็ตามหรือไม่
ขั้นตอนในการดำเนินการทดสอบ Chow
เราสามารถใช้ขั้นตอนต่อไปนี้เพื่อทำการทดสอบ Chow
ขั้นตอนที่ 1: กำหนดสมมติฐานว่างและทางเลือก
สมมติว่าเราใส่โมเดลการถดถอยต่อไปนี้กับชุดข้อมูลทั้งหมดของเรา:
- y t = a + bx 1t + cx t2 + ε
ต่อไป สมมติว่าเราแบ่งข้อมูลของเราออกเป็นสองกลุ่มตามจุดพักเชิงโครงสร้าง และปรับแบบจำลองการถดถอยต่อไปนี้ให้เหมาะกับแต่ละกลุ่ม:
- y t = a 1 + b 1 x 1t + c 1 x t2 + ε
- y t = a 2 + b 2 x 1t + c 2 x t2 + ε
เราจะใช้สมมติฐานว่างและทางเลือกต่อไปนี้สำหรับการทดสอบ Chow:
- ว่าง (H 0 ): a 1 = a 2 , b 1 = b 2 และ c 1 = c 2
- ทางเลือก ( HA ): การเปรียบเทียบอย่างน้อยหนึ่งรายการใน Null นั้นไม่เท่ากัน
หากเราปฏิเสธสมมติฐานว่าง เราก็มีหลักฐานเพียงพอที่จะบอกว่ามีจุดพักเชิงโครงสร้างในข้อมูล และเส้นการถดถอยสองเส้นสามารถใส่ข้อมูลได้ดีกว่าหนึ่งเส้น
หากเราไม่สามารถปฏิเสธสมมติฐานว่างได้ เราก็ไม่มีหลักฐานเพียงพอที่จะบอกว่ามีจุดพักเชิงโครงสร้างในข้อมูล ในกรณีนี้ เรากล่าวว่าเส้นการถดถอยสามารถ “รวม” ให้เป็นเส้นการถดถอยเส้นเดียวที่แสดงถึงรูปแบบของข้อมูลได้ดีเพียงพอ
ขั้นตอนที่ 2: คำนวณสถิติการทดสอบ
หากเรากำหนดเงื่อนไขดังต่อไปนี้:
- S T : ผลรวมของกำลังสองของข้อมูลที่เหลือทั้งหมด
- S 1 , S 2 : ผลรวมของกำลังสองของเศษที่เหลือของแต่ละกลุ่ม
- N 1 , N 2 : จำนวนการสังเกตในแต่ละกลุ่ม
- k: จำนวนพารามิเตอร์
จากนั้นเราสามารถพูดได้ว่าสถิติการทดสอบ Chow คือ:
สถิติการทดสอบ Chow = [(S T – (S 1 +S 2 ))/k] / [(S 1 +S 2 )/ (N 1 +N 2 -2k)]
สถิติการทดสอบนี้เป็นไปตามการแจกแจงแบบ F ด้วยดีกรีอิสระ k และ N 1 +N 2 -2k
ขั้นตอนที่ 3: ปฏิเสธหรือไม่ปฏิเสธสมมติฐานว่าง
หากค่า p ที่เกี่ยวข้องกับสถิติการทดสอบนี้ต่ำกว่า ระดับนัยสำคัญที่กำหนด เราสามารถปฏิเสธสมมติฐานว่างและสรุปได้ว่ามีจุดพักเชิงโครงสร้างในข้อมูล
โชคดีที่ซอฟต์แวร์ทางสถิติส่วนใหญ่สามารถทำการทดสอบ Chow ได้ ดังนั้นคุณอาจไม่ต้องทำการทดสอบด้วยตนเองเลย
ตัวอย่างการทำแบบทดสอบ Chow
โปรดดู บทช่วยสอนนี้ เพื่อดูตัวอย่างทีละขั้นตอนของวิธีดำเนินการทดสอบ Chow สำหรับชุดข้อมูลที่กำหนดใน R
บันทึกการทดสอบ Chow
ต่อไปนี้เป็นหมายเหตุบางประการที่ควรคำนึงถึงเกี่ยวกับการทดสอบ Chow:
1. การทดสอบจะถือว่าส่วนที่เหลือของแบบจำลองการถดถอยมีการกระจายอย่างเป็นอิสระและเหมือนกันจาก การแจกแจงแบบปกติ โดยไม่ทราบความแปรปรวน
2. การทดสอบ Chow ควรใช้เฉพาะเมื่อการแตกหักของโครงสร้างที่คุณต้องการทดสอบเกิดขึ้นในเวลา ที่ทราบเท่านั้น กล่าวอีกนัยหนึ่ง ไม่ควรใช้การทดสอบซ้ำๆ เพื่อพิจารณาว่าช่วงเวลาหนึ่งๆ ถือเป็นการแตกหักของโครงสร้างหรือไม่
เกี่ยวกับผู้แต่ง
ดร.เบนจามิน แอนเดอร์สัน
สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม