การวิเคราะห์องค์ประกอบหลักใน r: ตัวอย่างทีละขั้นตอน

การวิเคราะห์องค์ประกอบหลัก ซึ่งมักเรียกสั้น ๆ ว่า PCA เป็นเทคนิคการเรียนรู้ของเครื่องแบบ ไม่มีผู้ดูแล ซึ่งพยายามค้นหาองค์ประกอบหลัก ซึ่งได้แก่ การรวมกันเชิงเส้นของตัวทำนายดั้งเดิม ซึ่งอธิบายความแปรผันส่วนใหญ่ในชุดข้อมูล

เป้าหมายของ PCA คือการอธิบายความแปรปรวนส่วนใหญ่ในชุดข้อมูลที่มีตัวแปรน้อยกว่าชุดข้อมูลดั้งเดิม

สำหรับชุดข้อมูลที่กำหนดซึ่งมีตัวแปร p เราสามารถตรวจสอบแผนภูมิกระจายของตัวแปรแต่ละชุดรวมกันเป็นคู่ได้ แต่จำนวนแผนภูมิกระจายอาจมีขนาดใหญ่อย่างรวดเร็ว

สำหรับตัวทำนาย p จะมีเมฆจุด p(p-1)/2 จุด

ดังนั้น สำหรับชุดข้อมูลที่มีตัวทำนาย p = 15 ตัว จะมีแผนภาพกระจายที่แตกต่างกัน 105 แบบ!

โชคดีที่ PCA นำเสนอวิธีการในการค้นหาการแสดงชุดข้อมูลในมิติต่ำที่จับความแปรผันของข้อมูลให้ได้มากที่สุดเท่าที่จะเป็นไปได้

หากเราสามารถจับความแปรผันส่วนใหญ่ได้ในสองมิติ เราก็สามารถฉายภาพการสังเกตทั้งหมดจากชุดข้อมูลดั้งเดิมลงบนแผนภาพกระจายแบบธรรมดาได้

วิธีที่เราค้นหาส่วนประกอบหลักมีดังนี้:

_{รับ ชุด ข้อมูล ที่มี ตัวทำนาย} p : _

• _{ซี ม. = ΣΦ เจเอ็ม _}
• Z ₁ คือผลรวมเชิงเส้นของตัวทำนายที่จะจับความแปรปรวนให้ได้มากที่สุด
• Z ₂ คือผลรวมเชิงเส้นถัดไปของตัวทำนายที่จะจับความแปรปรวนมากที่สุดในขณะที่ ตั้งฉาก (กล่าวคือ ไม่สัมพันธ์กัน) กับ Z ₁
• Z ₃ คือผลรวมเชิงเส้นถัดไปของตัวทำนายที่จะจับความแปรปรวนมากที่สุดในขณะที่ตั้งฉากกับ Z ₂
• และอื่นๆ

ในทางปฏิบัติ เราใช้ขั้นตอนต่อไปนี้ในการคำนวณผลรวมเชิงเส้นของตัวทำนายดั้งเดิม:

1. ปรับขนาดตัวแปรแต่ละตัวให้มีค่าเฉลี่ยเป็น 0 และส่วนเบี่ยงเบนมาตรฐานเป็น 1

2. คำนวณเมทริกซ์ความแปรปรวนร่วมสำหรับตัวแปรที่ปรับขนาด

3. คำนวณค่าลักษณะเฉพาะของเมทริกซ์ความแปรปรวนร่วม

เมื่อใช้พีชคณิตเชิงเส้น เราสามารถแสดงว่าเวกเตอร์ลักษณะเฉพาะที่สอดคล้องกับค่าลักษณะเฉพาะที่ใหญ่ที่สุดนั้นเป็นองค์ประกอบหลักตัวแรก กล่าวอีกนัยหนึ่ง การผสมผสานตัวทำนายโดยเฉพาะนี้จะอธิบายความแปรปรวนที่ยิ่งใหญ่ที่สุดของข้อมูล

เวกเตอร์ลักษณะเฉพาะที่สอดคล้องกับค่าลักษณะเฉพาะที่ใหญ่เป็นอันดับสองคือองค์ประกอบหลักที่สอง เป็นต้น

บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีดำเนินการกระบวนการนี้ใน R

ขั้นตอนที่ 1: โหลดข้อมูล

ก่อนอื่นเราจะโหลดแพ็คเกจ Tidyverse ซึ่งมีฟังก์ชันที่มีประโยชน์มากมายสำหรับการแสดงภาพและจัดการข้อมูล:

 library (tidyverse)

สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูล USArrests ที่สร้างไว้ใน R ซึ่งมีจำนวนการจับกุมต่อผู้อยู่อาศัย 100,000 คนในแต่ละรัฐของสหรัฐอเมริกาในปี 1973 ในข้อหา ฆาตกรรม ทำร้ายร่างกาย และ ข่มขืน

นอกจากนี้ยังรวมเปอร์เซ็นต์ของประชากรแต่ละรัฐที่อาศัยอยู่ในเขตเมือง UrbanPop

รหัสต่อไปนี้แสดงวิธีการโหลดและแสดงแถวแรกของชุดข้อมูล:

 #load data
data ("USArrests")

#view first six rows of data
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7

ขั้นตอนที่ 2: คำนวณส่วนประกอบหลัก

หลังจากโหลดข้อมูลแล้ว เราสามารถใช้ฟังก์ชันในตัวของ R prcomp() เพื่อคำนวณส่วนประกอบหลักของชุดข้อมูลได้

อย่าลืมระบุ scale = TRUE เพื่อให้ตัวแปรแต่ละตัวในชุดข้อมูลได้รับการปรับขนาดให้มีค่าเฉลี่ยเป็น 0 และค่าเบี่ยงเบนมาตรฐานเป็น 1 ก่อนที่จะคำนวณองค์ประกอบหลัก

โปรดทราบว่าเวกเตอร์ลักษณะเฉพาะใน R ชี้ไปในทิศทางลบตามค่าเริ่มต้น ดังนั้นเราจะคูณด้วย -1 เพื่อกลับเครื่องหมาย

 #calculate main components
results <- prcomp(USArrests, scale = TRUE )

#reverse the signs
results$rotation <- -1*results$rotation

#display main components
results$rotation

               PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432

เราจะเห็นได้ว่าองค์ประกอบหลักตัวแรก (PC1) มีค่าสูงสำหรับการฆาตกรรม การทำร้ายร่างกาย และการข่มขืน ซึ่งบ่งชี้ว่าองค์ประกอบหลักนี้อธิบายถึงความแปรผันที่ยิ่งใหญ่ที่สุดของตัวแปรเหล่านี้

นอกจากนี้เรายังสามารถเห็นได้ว่าองค์ประกอบหลักที่สอง (PC2) มีมูลค่าสูงสำหรับ UrbanPop ซึ่งบ่งชี้ว่าองค์ประกอบหลักนี้เน้นที่ประชากรในเมือง

โปรดทราบว่าคะแนนองค์ประกอบหลักสำหรับแต่ละสถานะจะถูกเก็บไว้ใน results$x เราจะคูณคะแนนเหล่านี้ด้วย -1 เพื่อกลับเครื่องหมาย:

 #reverse the signs of the scores
results$x <- -1*results$x

#display the first six scores
head(results$x)

                  PC1 PC2 PC3 PC4
Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581
Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454
Arizona 1.7454429 0.7384595 -0.05423025 0.826264240
Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554
California 2.4986128 1.5274267 -0.59254100 0.338559240
Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164

ขั้นตอนที่ 3: เห็นภาพผลลัพธ์ด้วย biplot

ต่อไป เราสามารถสร้าง biplot ซึ่งเป็นพล็อตที่คาดการณ์แต่ละการสังเกตในชุดข้อมูลบน Scatterplot ที่ใช้ส่วนประกอบหลักที่หนึ่งและที่สองเป็นแกน:

โปรดทราบว่า มาตราส่วน = 0 ช่วยให้แน่ใจว่าลูกศรในพล็อตได้รับการปรับขนาดเพื่อแสดงการโหลด

 biplot(results, scale = 0 )

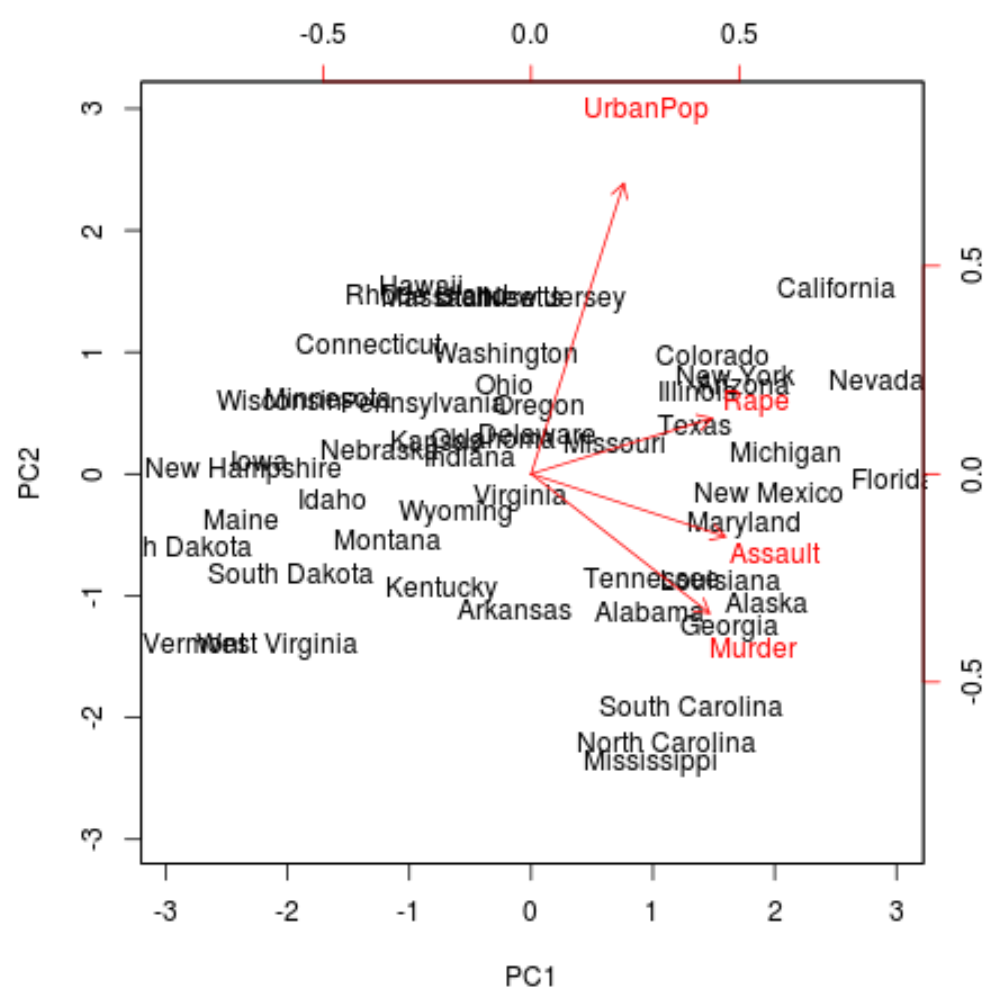
จากโครงเรื่อง เราจะเห็นแต่ละสถานะจาก 50 สถานะที่แสดงอยู่ในปริภูมิสองมิติที่เรียบง่าย

รัฐที่อยู่ใกล้กันบนกราฟมีรูปแบบข้อมูลที่คล้ายกันโดยคำนึงถึงตัวแปรในชุดข้อมูลดั้งเดิม

เรายังเห็นได้ว่าบางรัฐมีความเกี่ยวข้องอย่างมากกับอาชญากรรมบางประเภทมากกว่ารัฐอื่น ตัวอย่างเช่น จอร์เจียเป็นรัฐที่ใกล้เคียงที่สุดกับตัวแปร Murder ในโครงเรื่อง

หากเราดูรัฐที่มีอัตราการฆาตกรรมสูงสุดในชุดข้อมูลดั้งเดิม เราจะเห็นว่าจอร์เจียอยู่ในอันดับต้นๆ ของรายการ:

 #display states with highest murder rates in original dataset
head(USArrests[ order (-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia 17.4 211 60 25.8
Mississippi 16.1 259 44 17.1
Florida 15.4 335 80 31.9
Louisiana 15.4 249 66 22.2
South Carolina 14.4 279 48 22.5
Alabama 13.2 236 58 21.2

ขั้นตอนที่ 4: ค้นหาความแปรปรวนที่อธิบายโดยองค์ประกอบหลักแต่ละส่วน

เราสามารถใช้โค้ดต่อไปนี้เพื่อคำนวณความแปรปรวนรวมในชุดข้อมูลดั้งเดิมที่อธิบายโดยองค์ประกอบหลักแต่ละส่วน:

 #calculate total variance explained by each principal component
results$sdev^2 / sum (results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

จากผลลัพธ์เราสามารถสังเกตได้ดังต่อไปนี้:

• องค์ประกอบหลักแรกอธิบาย 62% ของความแปรปรวนทั้งหมดในชุดข้อมูล
• องค์ประกอบหลักที่สองอธิบาย 24.7% ของความแปรปรวนทั้งหมดในชุดข้อมูล
• องค์ประกอบหลักที่สามอธิบาย 8.9% ของความแปรปรวนทั้งหมดในชุดข้อมูล
• องค์ประกอบหลักที่สี่อธิบาย 4.3% ของความแปรปรวนทั้งหมดในชุดข้อมูล

ดังนั้น องค์ประกอบหลักสององค์ประกอบแรกจะอธิบายความแปรปรวนโดยรวมของข้อมูลเป็นส่วนใหญ่

นี่เป็นสัญญาณที่ดีเพราะแผนสองแผนก่อนหน้านี้คาดการณ์แต่ละข้อสังเกตจากข้อมูลต้นฉบับลงบนแผนกระจายที่พิจารณาเฉพาะองค์ประกอบหลักสององค์ประกอบแรกเท่านั้น

ดังนั้นจึงถูกต้องที่จะตรวจสอบรูปแบบใน biplot เพื่อระบุสถานะที่คล้ายคลึงกัน

นอกจากนี้เรายังสามารถสร้าง พล็อตหินกรวด ซึ่งเป็นกราฟที่แสดงความแปรปรวนทั้งหมดที่อธิบายโดยองค์ประกอบหลักแต่ละส่วน เพื่อให้เห็นภาพผลลัพธ์ PCA:

 #calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum (results$sdev^2)

#create scree plot
qplot(c(1:4), var_explained) + 
  geom_line() + 
  xlab(" Principal Component ") + 
  ylab(" Variance Explained ") +
  ggtitle(" Scree Plot ") +
  ylim(0, 1) 

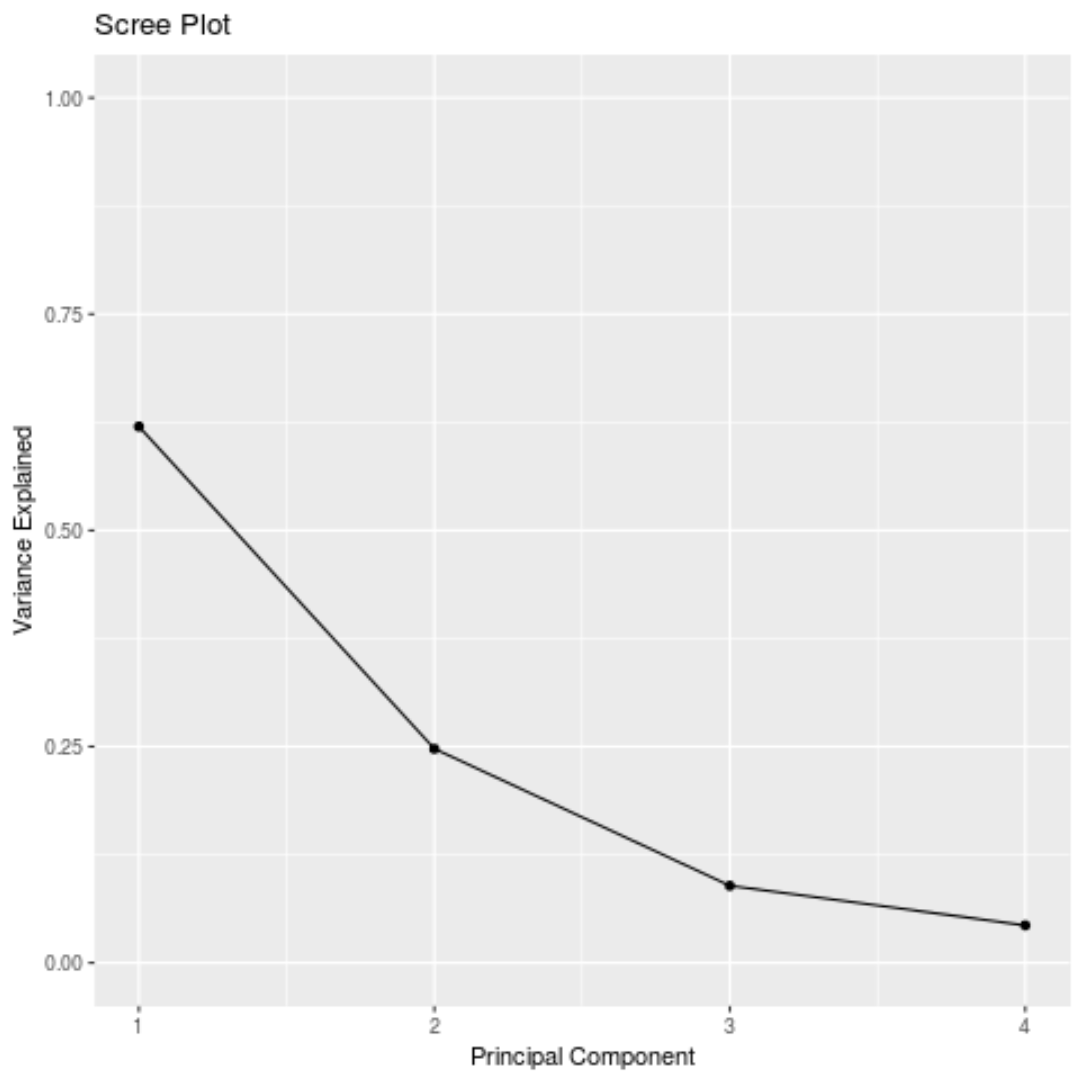
การวิเคราะห์องค์ประกอบหลักในทางปฏิบัติ

ในทางปฏิบัติ PCA ถูกใช้บ่อยที่สุดด้วยเหตุผลสองประการ:

1. การวิเคราะห์ข้อมูลเชิงสำรวจ เราใช้ PCA เมื่อสำรวจชุดข้อมูลเป็นครั้งแรก และต้องการทำความเข้าใจว่าข้อสังเกตใดในข้อมูลที่มีความคล้ายคลึงกันมากที่สุด

2. การถดถอยองค์ประกอบหลัก – เรายังสามารถใช้ PCA เพื่อคำนวณองค์ประกอบหลักซึ่งสามารถนำไปใช้ใน การถดถอยองค์ประกอบหลัก ได้ การถดถอยประเภทนี้มักใช้เมื่อมี multicollinearity ระหว่างตัวทำนายในชุดข้อมูล

รหัส R แบบเต็มที่ใช้ในบทช่วยสอนนี้สามารถพบได้ ที่นี่