การสุ่มตัวอย่างอย่างเป็นระบบ
ในบทความนี้ เราจะอธิบายว่าการสุ่มตัวอย่างอย่างเป็นระบบคืออะไร คุณลักษณะของมัน และดำเนินการอย่างไร คุณจะเห็นตัวอย่างการสุ่มตัวอย่างอย่างเป็นระบบด้วย นอกจากนี้ คุณจะได้เรียนรู้ว่าการสุ่มตัวอย่างอย่างเป็นระบบมีข้อดีและข้อเสียอย่างไร และควรใช้การสุ่มตัวอย่างประเภทนี้เมื่อใด
การสุ่มตัวอย่างอย่างเป็นระบบคืออะไร?
การสุ่มตัวอย่างอย่างเป็นระบบ เป็นวิธีความน่าจะเป็นที่ใช้ในการเลือกองค์ประกอบที่จะเป็นส่วนหนึ่งของกลุ่มตัวอย่างสำหรับการศึกษาทางสถิติ ในการสุ่มตัวอย่างอย่างเป็นระบบ องค์ประกอบหนึ่งจะถูกเลือกโดยการสุ่มก่อน และองค์ประกอบอื่นๆ ในตัวอย่างจะถูกเลือกตามช่วงเวลาที่คงที่
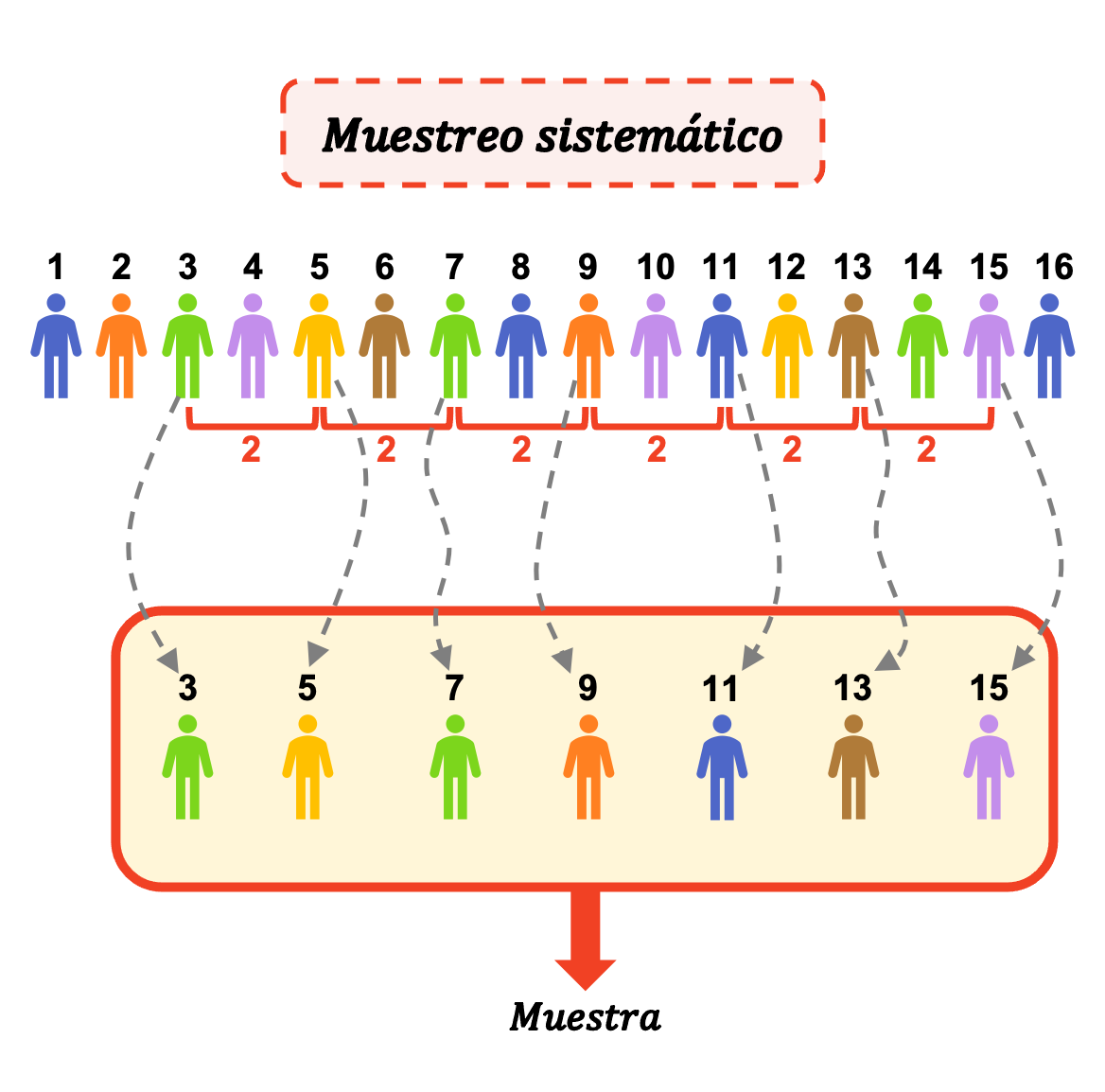
ดังนั้น ในการสุ่มตัวอย่างอย่างเป็นระบบ เมื่อเราสุ่มเลือกบุคคลแรกจากกลุ่มตัวอย่างแล้ว เราจะต้องนับจำนวนให้มากเท่ากับช่วงที่ต้องการเพื่อนำบุคคลถัดไปออกจากกลุ่มตัวอย่าง และเราทำซ้ำขั้นตอนเดียวกันอย่างต่อเนื่องจนกว่าเราจะมีบุคคลในกลุ่มตัวอย่างมากเท่ากับขนาดตัวอย่างที่เราต้องการ
ในทางกลับกัน คุณควรรู้ว่ามีวิธีการเพิ่มเติมในการเลือกบุคคลจากกลุ่มตัวอย่าง ประเภทการสุ่มตัวอย่างที่ใช้มากที่สุดคือ:
- การสุ่มตัวอย่างอย่างง่าย
- การสุ่มตัวอย่างแบบแบ่งชั้น
- การสุ่มตัวอย่างอย่างเป็นระบบ
- การสุ่มตัวอย่างคลัสเตอร์
ที่ probabilistica.com เรามีคำอธิบายโดยละเอียดเกี่ยวกับการสุ่มตัวอย่างความน่าจะเป็นแต่ละประเภท ดังนั้นหากคุณสนใจมากขึ้น คุณสามารถค้นหาวิธีดำเนินการแต่ละประเภทได้บนเว็บไซต์ของเรา
วิธีการสุ่มตัวอย่างอย่างเป็นระบบ
ขั้นตอนในการดำเนินการสุ่มตัวอย่างอย่างเป็นระบบมีดังนี้:
- กำหนดประชากรเป้าหมาย
- กำหนด ขนาดตัวอย่าง ที่ต้องการ
- คำนวณ ช่วงเวลาการสุ่มตัวอย่าง เมื่อต้องการทำเช่นนี้ ขนาดของประชากรจะถูกหารด้วยขนาดของกลุ่มตัวอย่าง
- สุ่มเลือก รายการแรกในกลุ่มตัวอย่าง
- เลือกองค์ประกอบที่เหลือของกลุ่มตัวอย่าง ในการดำเนินการนี้ ช่วงเวลาการสุ่มตัวอย่างจะถูกเพิ่มเข้ากับหมายเลขที่เลือกในขั้นตอนก่อนหน้าอย่างต่อเนื่อง
สิ่งสำคัญคือรายการแรกที่เลือกในการสุ่มตัวอย่างอย่างเป็นระบบจะต้องสุ่ม เนื่องจากจริงๆ แล้วเป็นรายการเดียวในกลุ่มตัวอย่างที่ถูกเลือกโดยการสุ่ม มิฉะนั้น ความสุ่มของการสุ่มตัวอย่างอย่างเป็นระบบจะได้รับผลกระทบ นี่คือเหตุผลที่ผู้วิจัยต้องแน่ใจว่าองค์ประกอบทั้งหมดของประชากรมีความน่าจะเป็นเท่ากันที่จะถูกเลือกเป็นจุดเริ่มต้น
ในทำนองเดียวกัน เนื่องจากองค์ประกอบตัวอย่างในการสุ่มตัวอย่างอย่างเป็นระบบจะถูกเลือกตามช่วงเวลา จึงอาจไม่มีองค์ประกอบบางประเภทในตัวอย่างสุดท้าย ดังนั้น ตัวอย่างจึงอาจเป็นตัวแทนได้ไม่เพียงพอ แต่นี่เป็นความเสี่ยงที่เราต้องเผชิญเมื่อเราดำเนินการสุ่มตัวอย่างอย่างเป็นระบบ
สุดท้ายนี้ คุณต้องคำนึงว่าช่วงการสุ่มตัวอย่างไม่ใช่แบบจำลอง เนื่องจากตัวอย่างที่เลือกจะไม่เพียงพอ และการศึกษาทางสถิติจะให้ผลลัพธ์ที่ไม่น่าเชื่อถือ
ตัวอย่างการสุ่มตัวอย่างอย่างเป็นระบบ
หลังจากเห็นคำจำกัดความของการสุ่มตัวอย่างอย่างเป็นระบบแล้ว เราจะมาอธิบายตัวอย่างของการสุ่มตัวอย่างประเภทนี้เพื่อให้คุณเข้าใจความหมายของการสุ่มตัวอย่างได้ดีขึ้น
ตัวอย่างเช่น หากเราต้องการดำเนินการสุ่มตัวอย่างอย่างเป็นระบบกับประชากร 1,000 องค์ประกอบเพื่อให้ได้ตัวอย่าง 50 องค์ประกอบ เราต้องดำเนินการดังต่อไปนี้
ขั้นแรก เราต้องคำนวณช่วงเวลาการสุ่มตัวอย่าง ในการดำเนินการนี้ เราเพียงแต่แบ่งขนาดประชากรด้วยขนาดกลุ่มตัวอย่าง:
![]()
ประการที่สอง เราต้องสุ่มเลือกวิชาแรกในกลุ่มตัวอย่าง ในการดำเนินการขั้นตอนนี้มีหลายวิธี แต่คุณสามารถใช้เช่นโปรแกรมคอมพิวเตอร์ Excel เพื่อรับตัวเลขสุ่มตั้งแต่ 1 ถึง 20 (ขอแนะนำให้ตัวเลขแรกอยู่ในส่วนแรก) สมมติว่าเราได้หมายเลข 17
![]()
ต่อไป เราต้องเพิ่มช่วงเวลาการสุ่มตัวอย่าง (20) ไปที่หมายเลข 17 เพื่อเลือกองค์ประกอบถัดไปจากตัวอย่าง เราต้องเลือกตัวเลขเพิ่มอีก 49 ตัว เนื่องจากขนาดตัวอย่างที่ต้องการคือ 50
![]()
เพื่อให้องค์ประกอบของประชากรที่ระบุด้วยตัวเลขที่ออกมาเป็นองค์ประกอบที่เลือกมาเป็นส่วนหนึ่งของกลุ่มตัวอย่างในการศึกษาทางสถิติ
ข้อดีและข้อเสียของการสุ่มตัวอย่างอย่างเป็นระบบ
การสุ่มตัวอย่างอย่างเป็นระบบมีข้อดีและข้อเสียดังต่อไปนี้:
| ข้อได้เปรียบ | ข้อเสีย |
|---|---|
| การสุ่มตัวอย่างอย่างเป็นระบบดำเนินการได้รวดเร็วมาก | หากมีรูปแบบและตรงกับช่วงการสุ่มตัวอย่าง คุณจะได้ตัวอย่างที่มีอคติ |
| มันง่ายที่จะเข้าใจ | ในตัวอย่างที่เลือก มีองค์ประกอบเดียวเท่านั้นที่ถูกสุ่มเลือก |
| โดยทั่วไปตัวอย่างที่ได้รับจะเป็นตัวแทน | เมื่อเลือกหัวข้อเริ่มต้นแล้ว บางรายการจะมีโอกาสถูกเลือกเป็นศูนย์ |
| การสุ่มตัวอย่างอย่างเป็นระบบไม่ได้จำกัดอยู่เพียงส่วนหนึ่งของประชากร แต่เป็นการสุ่มตัวอย่างองค์ประกอบที่กระจายไปทั่วประชากร | การประมาณค่าความแปรผันมีความซับซ้อนมากกว่าระบบสุ่มตัวอย่างแบบธรรมดา |
ตามที่เราเห็นในตัวอย่างข้างต้น การสุ่มตัวอย่างอย่างเป็นระบบทำได้รวดเร็วและง่ายดาย แม้ว่าอาจดูเหมือนไม่เป็นเช่นนั้น แต่ทรัพย์สินนี้มีความสำคัญเนื่องจากมีต้นทุนทางเศรษฐกิจที่ต่ำกว่า
ด้านบวกอีกประการหนึ่งของการสุ่มตัวอย่างอย่างเป็นระบบคือการสุ่มตัวอย่างจากประชากรทั้งหมด ในทางกลับกัน ในการสุ่มตัวอย่างประเภทอื่นๆ เราสามารถหาองค์ประกอบจากประชากรครึ่งแรกเท่านั้น
ข้อเสียของการสุ่มตัวอย่างอย่างเป็นระบบคือลำดับการวางองค์ประกอบของประชากรสามารถกำหนดเงื่อนไขความน่าเชื่อถือของผลลัพธ์ทางสถิติได้ เพราะหากมีช่วงเวลาหรือรูปแบบบางประเภท ก็อาจได้ตัวอย่างที่มีอคติได้ เช่น ถ้าเราเรียงลำดับประชากรชายและหญิงดังนี้
![]()
ด้วยคำสั่งนี้ หากเราใช้ช่วงการสุ่มตัวอย่างเป็น 2 เราจะเลือกเฉพาะผู้หญิงหรือผู้ชายเท่านั้น ขึ้นอยู่กับแหล่งกำเนิด ดังนั้นเราจึงจะได้ตัวอย่างที่ไม่น่าเชื่อถือ
สุดท้าย ด้านลบอีกประการหนึ่งของการสุ่มตัวอย่างอย่างเป็นระบบก็คือ มีเพียงองค์ประกอบเดียวเท่านั้นที่ถูกเลือกโดยการสุ่ม ซึ่งจะกำหนดเงื่อนไขให้กับองค์ประกอบที่เหลือในตัวอย่าง แตกต่างจากการสุ่มตัวอย่างประเภทอื่นๆ ที่มีโอกาสเกิดขึ้นมากกว่าตลอดกระบวนการ
เมื่อใดควรใช้การสุ่มตัวอย่างอย่างเป็นระบบ
สุดท้ายนี้ เราจะแสดงให้คุณเห็นว่าเมื่อใดที่ควรใช้การเก็บตัวอย่างอย่างเป็นระบบ และเมื่อใดไม่สามารถทำได้ เนื่องจากระบบการเก็บตัวอย่างนี้ไม่สามารถใช้งานได้เสมอไป
การสุ่มตัวอย่างอย่างเป็นระบบสามารถใช้ได้เมื่อจำเป็นต้องใช้วิธีการสุ่มตัวอย่างที่ง่ายและรวดเร็ว กล่าวอีกนัยหนึ่ง เมื่องบประมาณโครงการมีจำกัด การสุ่มตัวอย่างอย่างเป็นระบบถือเป็นตัวเลือกที่ดีมาก เนื่องจากต้องใช้ทรัพยากรเพียงเล็กน้อยในการดำเนินการ
ดังที่เราได้เห็นในบทความแล้ว การใช้การสุ่มตัวอย่างประเภทนี้เมื่อประชากรแสดงรูปแบบบางประเภทนั้นไม่เหมาะสม เนื่องจากสามารถได้ตัวอย่างที่มีอคติได้
ท้ายที่สุด หากมีกลุ่มที่แตกต่างกันจำนวนมากในประชากร หรืออีกนัยหนึ่ง หากมีหลายชั้น ก็ควรใช้การสุ่มตัวอย่างแบบแบ่งชั้น เนื่องจากช่วยให้วิเคราะห์ทางสถิติของชั้นต่างๆ แยกกันได้ ซึ่งไม่อนุญาตให้มีการสุ่มตัวอย่างอย่างเป็นระบบ