คู่มือฉบับสมบูรณ์: การออกแบบแฟกทอเรียล 2×4

การออกแบบแฟกทอเรียล 2 × 4 คือการออกแบบเชิงทดลองประเภทหนึ่งที่ช่วยให้นักวิจัยเข้าใจผลกระทบของตัวแปรอิสระสองตัวต่อตัวแปรตามตัวเดียว

ในการออกแบบประเภทนี้ ตัวแปรอิสระตัวหนึ่งมีสอง ระดับ และตัวแปรอิสระตัวอื่นมีสี่ระดับ

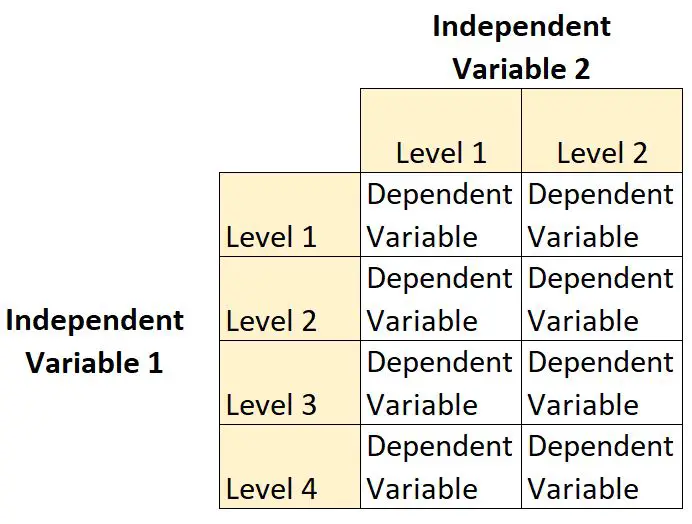
ตัวอย่างเช่น สมมติว่านักพฤกษศาสตร์ต้องการเข้าใจผลกระทบของแสงแดด (ไม่มี ต่ำ ปานกลาง หรือสูง) และความถี่ในการรดน้ำ (รายวันหรือรายสัปดาห์) ต่อการเจริญเติบโตของพืชบางชนิด

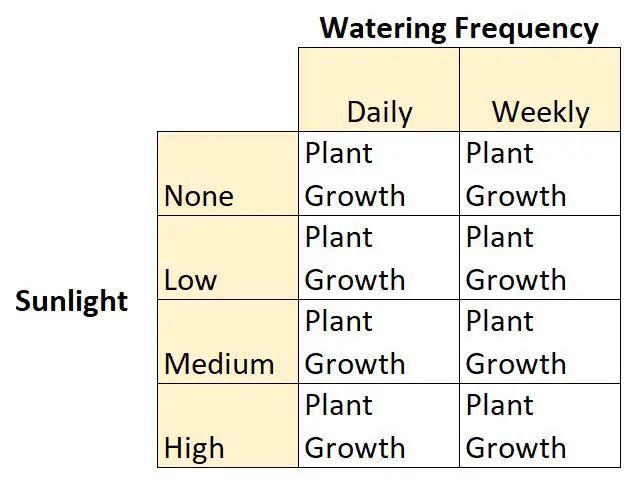
นี่คือตัวอย่างของการออกแบบแฟคทอเรียล 2 × 4 เนื่องจากมีตัวแปรอิสระสองตัว ตัวแปรหนึ่งมีสองระดับและอีกตัวหนึ่งมีสี่ระดับ:

• ตัวแปรอิสระ #1: แสงแดด
  • ระดับ: ไม่มี, ต่ำ, ปานกลาง, สูง
• ตัวแปรอิสระ #2: ความถี่ในการรดน้ำ
  • ระดับ: รายวัน รายสัปดาห์

และมีตัวแปรตาม: การเจริญเติบโตของพืช

จุดประสงค์ของการออกแบบแฟกทอเรียลขนาด 2 × 4

การออกแบบแฟกทอเรียล 2×4 ช่วยให้สามารถวิเคราะห์ผลกระทบต่อไปนี้:

ผลกระทบหลัก: สิ่งเหล่านี้คือผลกระทบที่ตัวแปรอิสระตัวเดียวมีต่อตัวแปรตาม

ตัวอย่างเช่น ในสถานการณ์ก่อนหน้านี้ เราสามารถวิเคราะห์ผลกระทบหลักต่อไปนี้:

• ผลกระทบหลักของแสงแดดต่อการเจริญเติบโตของพืช
  • การเจริญเติบโตเฉลี่ยของพืชทุกชนิดที่ไม่ได้รับแสงแดด
  • การเจริญเติบโตเฉลี่ยของพืชทุกชนิดที่ได้รับแสงแดดน้อย
  • การเจริญเติบโตเฉลี่ยของพืชทุกชนิดที่ได้รับแสงแดดเฉลี่ย
  • การเจริญเติบโตเฉลี่ยของพืชทุกชนิดที่ได้รับแสงแดดสูง
• ผลกระทบหลักของความถี่ในการรดน้ำต่อการเจริญเติบโตของพืช
  • การเจริญเติบโตเฉลี่ยของพืชทุกชนิดที่รดน้ำทุกวัน
  • การเจริญเติบโตโดยเฉลี่ยของพืชทุกชนิดที่รดน้ำในแต่ละสัปดาห์

ผลกระทบจากปฏิสัมพันธ์: เกิดขึ้นเมื่อผลกระทบของตัวแปรอิสระตัวหนึ่งต่อตัวแปรตามขึ้นอยู่กับระดับของตัวแปรอิสระตัวอื่น

ตัวอย่างเช่น ในสถานการณ์ก่อนหน้านี้ เราสามารถวิเคราะห์ผลกระทบจากการโต้ตอบต่อไปนี้:

• ผลของแสงแดดต่อการเจริญเติบโตของพืชขึ้นอยู่กับความถี่ในการรดน้ำหรือไม่?
• ผลของความถี่ในการรดน้ำต่อการเจริญเติบโตของพืชขึ้นอยู่กับแสงแดดหรือไม่?

วิธีการวิเคราะห์การออกแบบแฟคทอเรียล 2 × 4

เราสามารถใช้การวิเคราะห์ ความแปรปรวนแบบสองทาง เพื่อทดสอบอย่างเป็นทางการว่าตัวแปรอิสระมีความสัมพันธ์ที่มีนัยสำคัญทางสถิติกับตัวแปรตามหรือไม่

ตัวอย่างเช่น รหัสต่อไปนี้แสดงวิธีดำเนินการวิเคราะห์ความแปรปรวนแบบสองทางสำหรับสถานการณ์โรงงานสมมุติของเราใน R:

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' None ', ' Low ', ' Medium ', ' High '), each= 10 , times= 2 ),
                 water = rep(c(' Daily ', ' Weekly '), each= 40 , times= 2 ),
                 growth = c(rnorm(10, 8, 2), rnorm(10, 8, 3), rnorm(10, 13, 2),
                            rnorm(10, 14, 3), rnorm(10, 10, 4), rnorm(10, 12, 3),
                            rnorm(10, 13, 2), rnorm(10, 14, 4)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 3 744.1 248.04 34.16 < 2e-16 ***
water 1 43.1 43.05 5.93 0.016 *  
sunlight:water 3 195.8 65.27 8.99 1.61e-05 ***
Residuals 152 1103.5 7.26                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

วิธีการตีความผลลัพธ์ ANOVA มีดังนี้

ผลกระทบหลัก #1 (แสงแดด) : ค่า p ที่เกี่ยวข้องกับแสงแดดคือ <2e-16 เนื่องจากตัวเลขนี้น้อยกว่า 0.05 หมายความว่าการได้รับแสงแดดมีผลกระทบที่มีนัยสำคัญทางสถิติต่อการเจริญเติบโตของพืช

ผลกระทบหลัก #2 (น้ำ) : ค่า p ที่เกี่ยวข้องกับน้ำคือ 0.016 เนื่องจากตัวเลขนี้น้อยกว่า 0.05 หมายความว่าความถี่ในการรดน้ำก็มีผลกระทบที่มีนัยสำคัญทางสถิติต่อการเจริญเติบโตของพืชเช่นกัน

ผลกระทบจากปฏิสัมพันธ์ : ค่า p ของปฏิสัมพันธ์ระหว่างแสงแดดกับน้ำคือ 0.000061 เนื่องจากค่านี้น้อยกว่า 0.05 หมายความว่ามีผลกระทบต่อปฏิสัมพันธ์ระหว่างแสงแดดและน้ำ

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับการออกแบบและการวิเคราะห์การทดลอง:

คู่มือฉบับสมบูรณ์: การออกแบบแฟกทอเรียล 2 × 2
คู่มือฉบับสมบูรณ์: การออกแบบแฟกทอเรียล 2 × 3
แฟกทอเรียล ANOVA คืออะไร?