Excel: สร้างการเปรียบเทียบทางสถิติของชุดข้อมูลสองชุด

บ่อยครั้ง คุณอาจต้องการทำการเปรียบเทียบทางสถิติของชุดข้อมูลสองชุดใน Excel เพื่อทำความเข้าใจว่าการกระจายค่าในแต่ละชุดข้อมูลแตกต่างกันอย่างไร

มีสองวิธีทั่วไปในการเปรียบเทียบทางสถิติ:

วิธีที่ 1: คำนวณสรุปห้าหลักของชุดข้อมูลแต่ละชุด

เราสามารถคำนวณสรุปตัวเลขห้าตัวของแต่ละชุดข้อมูลซึ่งประกอบด้วยค่าต่อไปนี้

• ค่าต่ำสุด
• ควอร์ไทล์ที่หนึ่ง (เปอร์เซ็นไทล์ที่ 25)
• ค่ามัธยฐาน (เปอร์เซ็นไทล์ที่ 50)
• ควอไทล์ที่สาม (เปอร์เซ็นไทล์ที่ 75)
• สูงสุด

ด้วยการคำนวณค่าทั้งห้านี้ เราจะสามารถเข้าใจการกระจายของค่าในแต่ละชุดข้อมูลได้ดี

วิธีที่ 2: คำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน

วิธีที่ง่ายกว่าในการเปรียบเทียบทางสถิติของชุดข้อมูลสองชุดคือการคำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของชุดข้อมูลแต่ละชุด

สิ่งนี้ช่วยให้เราเข้าใจโดยประมาณว่าค่า “ส่วนกลาง” อยู่ที่ไหน และการกระจายของค่าคืออะไรในแต่ละชุดข้อมูล

ตัวอย่างต่อไปนี้แสดงวิธีการใช้แต่ละวิธีในทางปฏิบัติ

ตัวอย่าง: ทำการเปรียบเทียบทางสถิติของข้อมูลสองชุดใน Excel

สมมติว่าเรามีข้อมูลสองชุดใน Excel ที่แสดงผลของนักเรียนจากสองชั้นเรียนที่แตกต่างกันที่ได้รับจากการสอบเฉพาะ:

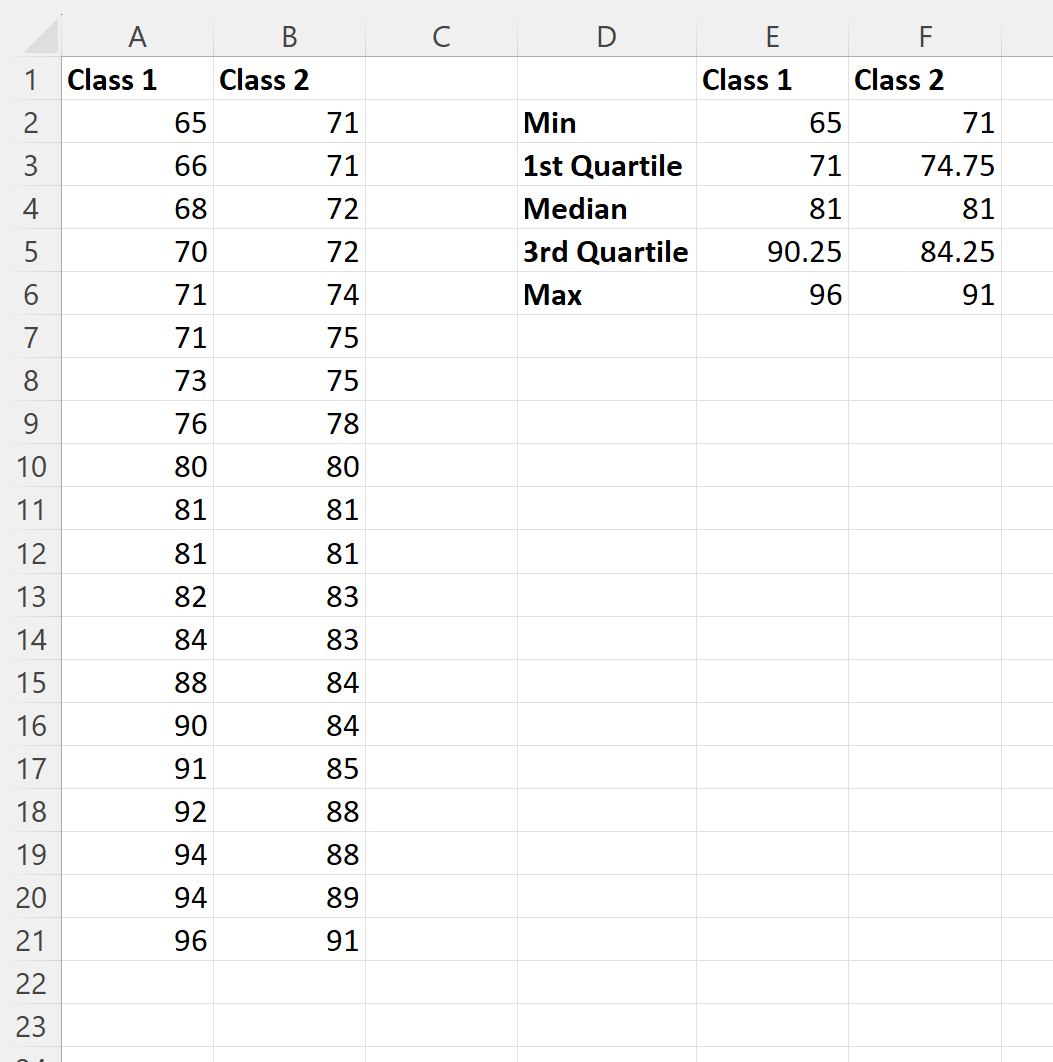
เราสามารถพิมพ์สูตรต่อไปนี้ลงในเซลล์ของคอลัมน์ E เพื่อคำนวณผลสรุปการสอบห้าหลักสำหรับชั้นเรียน 1:

• E2 : =นาที(A2:A21)
• E3 : =ควอไทล์(A2:A21, 1)
• E4 : =ค่ามัธยฐาน(A2:A21)
• E5 : =ควอไทล์(A2:A21, 3)
• E6 : =สูงสุด(A2:A21

จากนั้นเราสามารถคลิกและลากสูตรเหล่านี้ไปทางขวาเพื่อคำนวณค่าเดียวกันสำหรับคลาส 2:

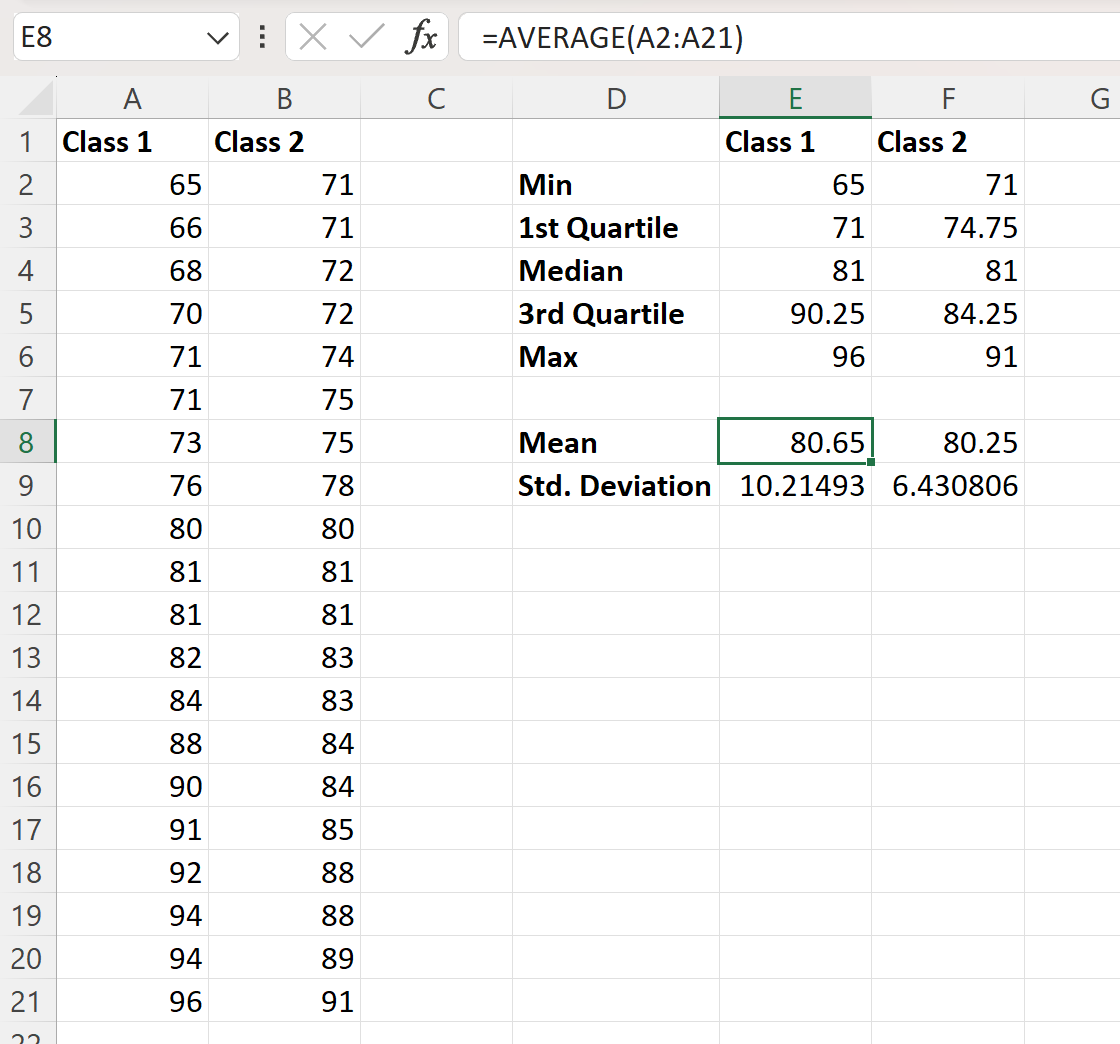
จากนั้นเราสามารถป้อนสูตรต่อไปนี้ลงในเซลล์ของคอลัมน์ E เพื่อคำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของผลการสอบสำหรับคลาส 1:

• E8 : =ค่าเฉลี่ย(A2:A21)
• E9 : =ETDEV(A2:A21, 1)

จากนั้นเราสามารถคลิกและลากสูตรเหล่านี้ไปทางขวาเพื่อคำนวณค่าเดียวกันสำหรับคลาส 2:

เราสามารถสรุปได้ดังต่อไปนี้จากการเปรียบเทียบทางสถิติของชุดข้อมูลทั้งสองนี้:

ข้อสรุปที่ 1: ชุดข้อมูลทั้งสองชุดมีค่า “แกนกลาง” ที่คล้ายคลึงกัน

ชุดข้อมูลทั้งสองชุดมีคะแนนสอบเฉลี่ยอยู่ที่ 81 โดยค่าเฉลี่ยต่างกันเพียงเล็กน้อย โดยชั้นที่ 1 มีคะแนนสอบเฉลี่ย 80.65 ในขณะที่ชั้นที่ 2 มีคะแนนสอบเฉลี่ย 80.65 ในขณะที่ชั้นที่ 2 มีคะแนนสอบเฉลี่ยอยู่ที่ 80.65 80.65 ‘ ทบทวน 80.25

สิ่งนี้บอกเราว่าคะแนนสอบ “หลัก” หรือ “ทั่วไป” ระหว่างทั้งสองชั้นเรียนมีความคล้ายคลึงกัน

ข้อสรุปที่ 2: ชุดข้อมูลชุดแรกมี “การกระจาย” ของค่าที่ใหญ่กว่ามาก

ตัวชี้วัดหลายตัวบอกเราว่าผลการสอบชั้นหนึ่งมีการกระจายมากกว่าการสอบชั้นสองมาก

ตัวอย่างเช่น ขอบเขตของคลาส 1 นั้นสูงกว่ามาก:

• ช่วงคลาส 1: 96 – 65 = 31
• ช่วงคลาส 2: 91 – 71 = 20

ช่วงระหว่างควอไทล์ของคลาส 1 ก็สูงกว่ามากเช่นกัน:

• ช่วงระหว่างควอไทล์คลาส 1: 90.25 – 71 = 19.25
• ช่วงระหว่างควอไทล์คลาส 2: 84.25 – 74.75 = 9.5

ค่าเบี่ยงเบนมาตรฐานของคลาส 1 ก็สูงกว่ามากเช่นกัน:

• ส่วนเบี่ยงเบนมาตรฐานคลาส 1: 10.21
• ส่วนเบี่ยงเบนมาตรฐานของคลาส 2: 6.43

แต่ละมาตรการเหล่านี้บอกเราว่าช่องว่างของคะแนนสอบสำหรับนักเรียนรุ่นที่ 1 นั้นสูงกว่าช่องว่างของคะแนนสอบสำหรับรุ่นที่ 2 มาก

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการทั่วไปอื่นๆ ใน Excel:

วิธีสร้างตารางสรุปใน Excel
วิธีการคำนวณค่ามัธยฐานตามกลุ่มใน Excel
วิธีการคำนวณค่าเบี่ยงเบนมาตรฐานและละเว้นศูนย์ใน Excel