วิธีการแก้ไข bonferroni ใน r

การวิเคราะห์ความแปรปรวนแบบทางเดียว ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่

หากค่า p-value โดยรวมของตาราง ANOVA ต่ำกว่าระดับนัยสำคัญที่กำหนด เราก็มีหลักฐานเพียงพอที่จะบอกว่าค่าเฉลี่ยของกลุ่มอย่างน้อยหนึ่งรายการแตกต่างจากค่าเฉลี่ยอื่นๆ

อย่างไรก็ตาม นี่ไม่ได้บอกเราว่ากลุ่ม ใด มีความแตกต่างกัน นี่บอกเราว่าค่าเฉลี่ยกลุ่มไม่เท่ากันทั้งหมด

หากต้องการทราบว่ากลุ่มใดมีความแตกต่างกัน เราต้องทำการทดสอบทีแบบคู่ระหว่างแต่ละกลุ่ม พร้อมกับควบคุม อัตราข้อผิดพลาดตามครอบครัว

วิธีหนึ่งที่พบบ่อยที่สุดในการบรรลุเป้าหมายนี้คือการใช้ การแก้ไข Bonferroni เมื่อคำนวณค่า p สำหรับการทดสอบทีแบบคู่แต่ละครั้ง

บทช่วยสอนนี้จะอธิบายวิธีการแก้ไข Bonferroni ใน R

ตัวอย่าง: การแก้ไข Bonferroni ใน R

สมมติว่าครูต้องการทราบว่าเทคนิคการเรียนสามแบบที่แตกต่างกันนำไปสู่คะแนนสอบที่แตกต่างกันของนักเรียนหรือไม่

เพื่อทดสอบสิ่งนี้ เธอสุ่มมอบหมายให้นักเรียน 10 คนใช้เทคนิคการเรียนรู้แต่ละอย่าง หลังจากใช้เทคนิคการเรียนที่ได้รับมอบหมายมาหนึ่งสัปดาห์ นักเรียนแต่ละคนจะสอบแบบเดียวกัน

เราสามารถใช้ขั้นตอนต่อไปนี้ใน R เพื่อให้พอดีกับการวิเคราะห์ความแปรปรวนแบบทางเดียว และใช้การแก้ไข Bonferroni เพื่อคำนวณความแตกต่างแบบคู่ระหว่างผลการสอบของแต่ละกลุ่ม

ขั้นตอนที่ 1: สร้างชุดข้อมูล

รหัสต่อไปนี้แสดงวิธีสร้างชุดข้อมูลที่มีผลการสอบของนักเรียนทั้ง 30 คน:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

ขั้นตอนที่ 2: ดูผลการสอบของแต่ละกลุ่ม

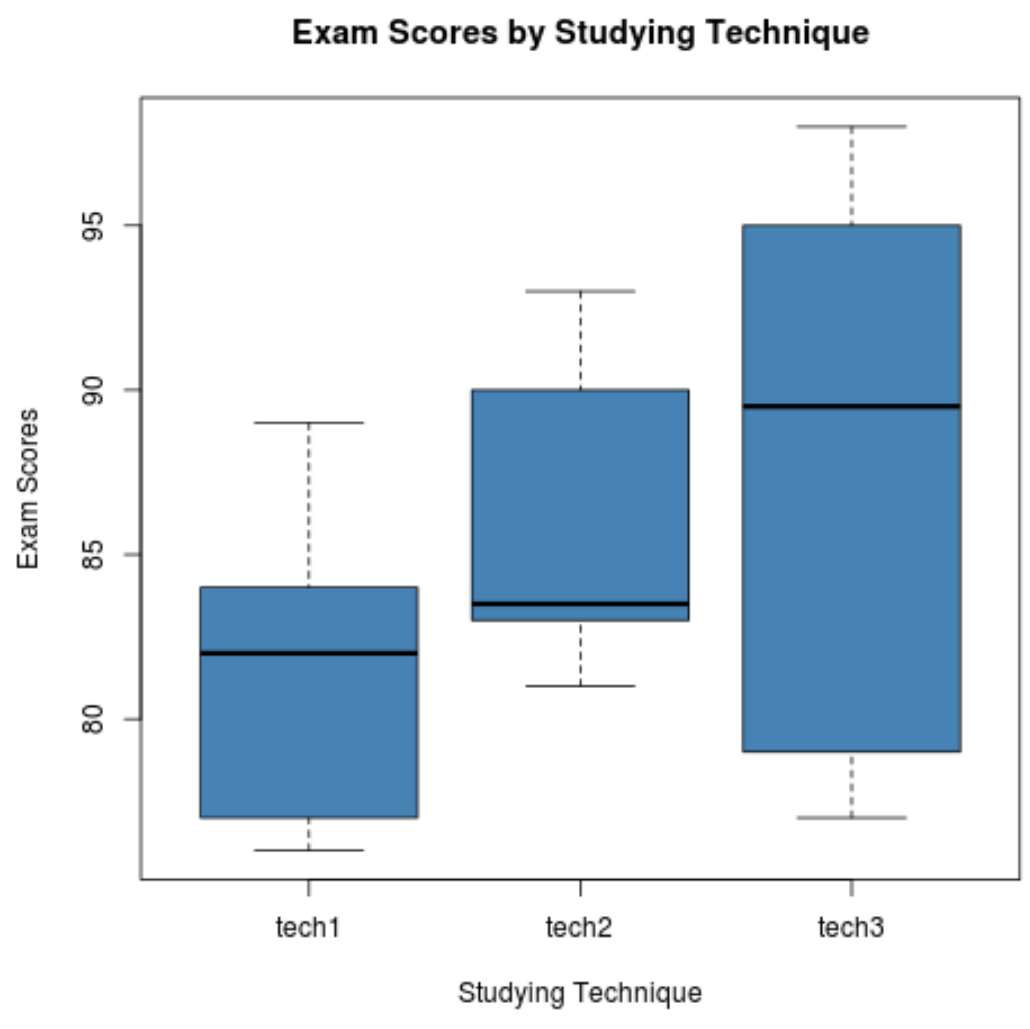
รหัสต่อไปนี้แสดงวิธีสร้าง boxplots เพื่อให้เห็นภาพการกระจายผลการสอบสำหรับแต่ละกลุ่ม:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

ขั้นตอนที่ 3: ดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียว

รหัสต่อไปนี้แสดงวิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อทดสอบความแตกต่างระหว่างคะแนนสอบเฉลี่ยในแต่ละกลุ่ม:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

เนื่องจากค่า p-value โดยรวม ( 0.0476 ) น้อยกว่า 0.05 แสดงว่าแต่ละกลุ่มมีคะแนนสอบเฉลี่ยไม่เท่ากัน

ต่อไป เราจะทำการทดสอบทีแบบคู่โดยใช้การแก้ไข Bonferroni สำหรับค่า p เพื่อคำนวณความแตกต่างแบบคู่ระหว่างผลการสอบของแต่ละกลุ่ม

ขั้นตอนที่ 4: ทำการทดสอบทีแบบคู่

ในการดำเนินการทดสอบค่าทีแบบคู่ด้วยการแก้ไข Bonferroni ใน R เราสามารถใช้ฟังก์ชัน pairwise.t.test() ซึ่งใช้ไวยากรณ์ต่อไปนี้:

pairwise.t.test(x, g, p.adjust.method=”bonferroni”)

ทอง:

• x: เวกเตอร์ตัวเลขของค่าตอบสนอง
• g: เวกเตอร์ที่ระบุชื่อกลุ่ม (เช่น เทคนิคการศึกษา)

รหัสต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้สำหรับตัวอย่างของเรา:

 #perform pairwise t-tests with Bonferroni's correction
pairwise.t.test(data$score, data$technique, p.adjust.method=" bonferroni ")

	Pairwise comparisons using t tests with pooled SD 

data: data$score and data$technique 

      tech1 tech2
tech2 0.309 -    
tech3 0.048 1.000

P value adjustment method: bonferroni

วิธีการตีความผลลัพธ์มีดังนี้:

• ค่า p ที่ปรับแล้วสำหรับผลต่างเฉลี่ยของคะแนนสอบระหว่างเทคนิคที่ 1 และเทคนิคที่ 2 คือ 0.309
• ค่า p ที่ปรับแล้วสำหรับผลต่างเฉลี่ยของคะแนนสอบระหว่างเทคนิคที่ 1 และเทคนิคที่ 3 คือ 0.048
• ค่า p ที่ปรับแล้วสำหรับผลต่างเฉลี่ยของคะแนนสอบระหว่างเทคนิคที่ 2 และเทคนิคที่ 3 คือ 1,000

จากผลลัพธ์ เราจะเห็นว่าความแตกต่างที่มีนัยสำคัญเพียงอย่างเดียวคือระหว่างเทคนิคที่ 1 และเทคนิคที่ 3

แหล่งข้อมูลเพิ่มเติม

ข้อมูลเบื้องต้นเกี่ยวกับการวิเคราะห์ความแปรปรวนแบบทางเดียว
วิธีดำเนินการวิเคราะห์ความแปรปรวนแบบทางเดียวใน R
วิธีทำการทดสอบ Tukey ใน R
วิธีทำการทดสอบ Dunnett ใน R