คำอธิบายง่ายๆ เกี่ยวกับการแก้ไขความต่อเนื่องในสถิติ
การแก้ไขความต่อเนื่อง จะใช้เมื่อคุณต้องการใช้การแจกแจงแบบต่อเนื่องเพื่อประมาณการแจกแจงแบบไม่ต่อเนื่อง โดยทั่วไปจะใช้เมื่อคุณต้องการใช้ การแจกแจงแบบปกติ เพื่อประมาณค่า การแจกแจงแบบทวินาม
โปรดจำไว้ว่าการแจกแจงแบบทวินามบอกเราถึงความน่าจะเป็นที่จะประสบความสำเร็จ x ในการทดลอง n ครั้ง โดยพิจารณาว่าความน่าจะเป็นที่จะประสบความสำเร็จในการทดลองครั้งเดียวคือ p ในการตอบคำถามเกี่ยวกับความน่าจะเป็นด้วยการแจกแจงแบบทวินาม เราก็แค่ใช้ เครื่องคำนวณการแจกแจงแบบทวินาม แต่เราก็ ประมาณ ความน่าจะเป็นได้โดยใช้การแจกแจงแบบปกติพร้อมการแก้ไขความต่อเนื่อง
การแก้ไขความต่อเนื่องคือชื่อที่กำหนดให้กับ การบวกหรือลบ 0.5 จากค่า x ที่ไม่ต่อเนื่อง
ตัวอย่างเช่น สมมติว่าเราต้องการหาความน่าจะเป็นที่เหรียญจะตกหัวน้อยกว่าหรือเท่ากับ 45 ครั้งในการเสี่ยง 100 ครั้ง นั่นคือเราต้องการหา P(X ≤ 45) หากต้องการใช้การแจกแจงแบบปกติเพื่อประมาณค่าการแจกแจงแบบทวินาม เราจะหา P(X ≤ 45.5) แทน
ตารางต่อไปนี้แสดงเวลาที่คุณควรบวกหรือลบ 0.5 ขึ้นอยู่กับประเภทของความน่าจะเป็นที่คุณพยายามค้นหา:
| ใช้การแจกแจงแบบทวินาม | การใช้การแจกแจงแบบปกติพร้อมการแก้ไขความต่อเนื่อง |
|---|---|
| เอ็กซ์ = 45 | 44.5 < X < 45.5 |
| เอ็กซ์ ≤ 45 | เอ็กซ์ < 45.5 |
| เอ็กซ์ < 45 | เอ็กซ์ < 44.5 |
| X ≥ 45 | เอ็กซ์ > 44.5 |
| เอ็กซ์ > 45 | เอ็กซ์ > 45.5 |
บันทึก:
ควรใช้การแก้ไขความต่อเนื่องกับการแจกแจงแบบปกติเพื่อประมาณค่าการแจกแจงแบบทวินาม เมื่อ n*p และ n*(1-p) มีค่าอย่างน้อย 5 ทั้งคู่
ตัวอย่างเช่น สมมติว่า n = 15 และ p = 0.6 ในกรณีนี้:
n*p = 15 * 0.6 = 9
n*(1-p) = 15 * (1 – 0.6) = 15 * (0.4) = 6
เนื่องจากตัวเลขทั้งสองนี้มากกว่าหรือเท่ากับ 5 จึงเป็นที่ยอมรับได้ที่จะใช้การแก้ไขความต่อเนื่องในสถานการณ์นี้
ตัวอย่างต่อไปนี้แสดงวิธีใช้การแก้ไขความต่อเนื่องกับการแจกแจงแบบปกติเพื่อประมาณค่าการแจกแจงแบบทวินาม
ตัวอย่างการประยุกต์ใช้การแก้ไขความต่อเนื่อง
สมมติว่าเราต้องการทราบความน่าจะเป็นที่เหรียญจะตกบนหัวน้อยกว่าหรือเท่ากับ 43 ครั้งในการโยน 100 ครั้ง ในกรณีนี้:
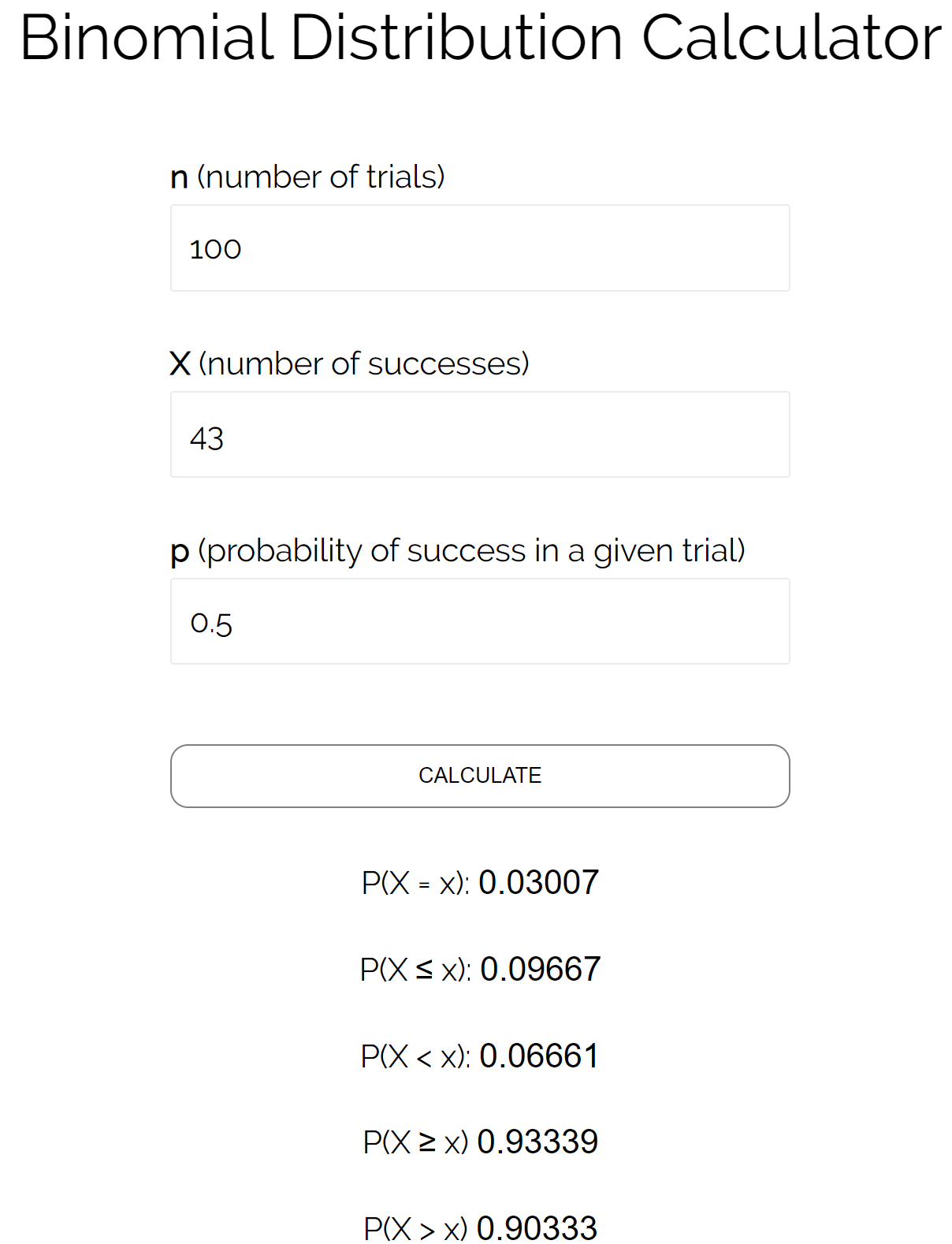
n = จำนวนการทดลอง = 100
X = จำนวนความสำเร็จ = 43
p = ความน่าจะเป็นที่จะประสบความสำเร็จในการทดลองที่กำหนด = 0.50
เราสามารถแทนค่าตัวเลขเหล่านี้ลงใน เครื่องคำนวณการกระจายตัวแบบทวินาม เพื่อดูว่าความน่าจะเป็นที่เหรียญตกบนหัวน้อยกว่าหรือเท่ากับ 43 เท่าคือ 0.09667
หากต้องการประมาณการแจกแจงแบบทวินามโดยใช้การแก้ไขความต่อเนื่องกับการแจกแจงแบบปกติ เราสามารถใช้ขั้นตอนต่อไปนี้:
ขั้นตอนที่ 1: ตรวจสอบว่า n*p และ n*(1-p) มีอย่างน้อย 5 ทั้งคู่
n*p = 100*0.5 = 50
n*(1-p) = 100*(1 – 0.5) = 100*0.5 = 50
ทั้งสองจำนวนมากกว่าหรือเท่ากับ 5 เราก็เลยไปต่อได้
ขั้นตอนที่ 2: พิจารณาว่าจะเพิ่มหรือลบ 0.5
จากตารางด้านบน เราจะเห็นว่าเราควร บวก 0.5 เมื่อเราทำงานกับความน่าจะเป็นในรูปของ X ≤ 43 ดังนั้น เราจะพบ P(X< 43.5)
ขั้นตอนที่ 3: ค้นหาค่าเฉลี่ย (μ) และส่วนเบี่ยงเบนมาตรฐาน (σ) ของการแจกแจงแบบทวินาม
µ = n*p = 100*0.5 = 50
σ = √ n*p*(1-p) = √ 100*.5*(1-.5) = √ 25 = 5
ขั้นตอนที่ 4: ค้นหาคะแนน z โดยใช้ค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานที่พบในขั้นตอนก่อนหน้า
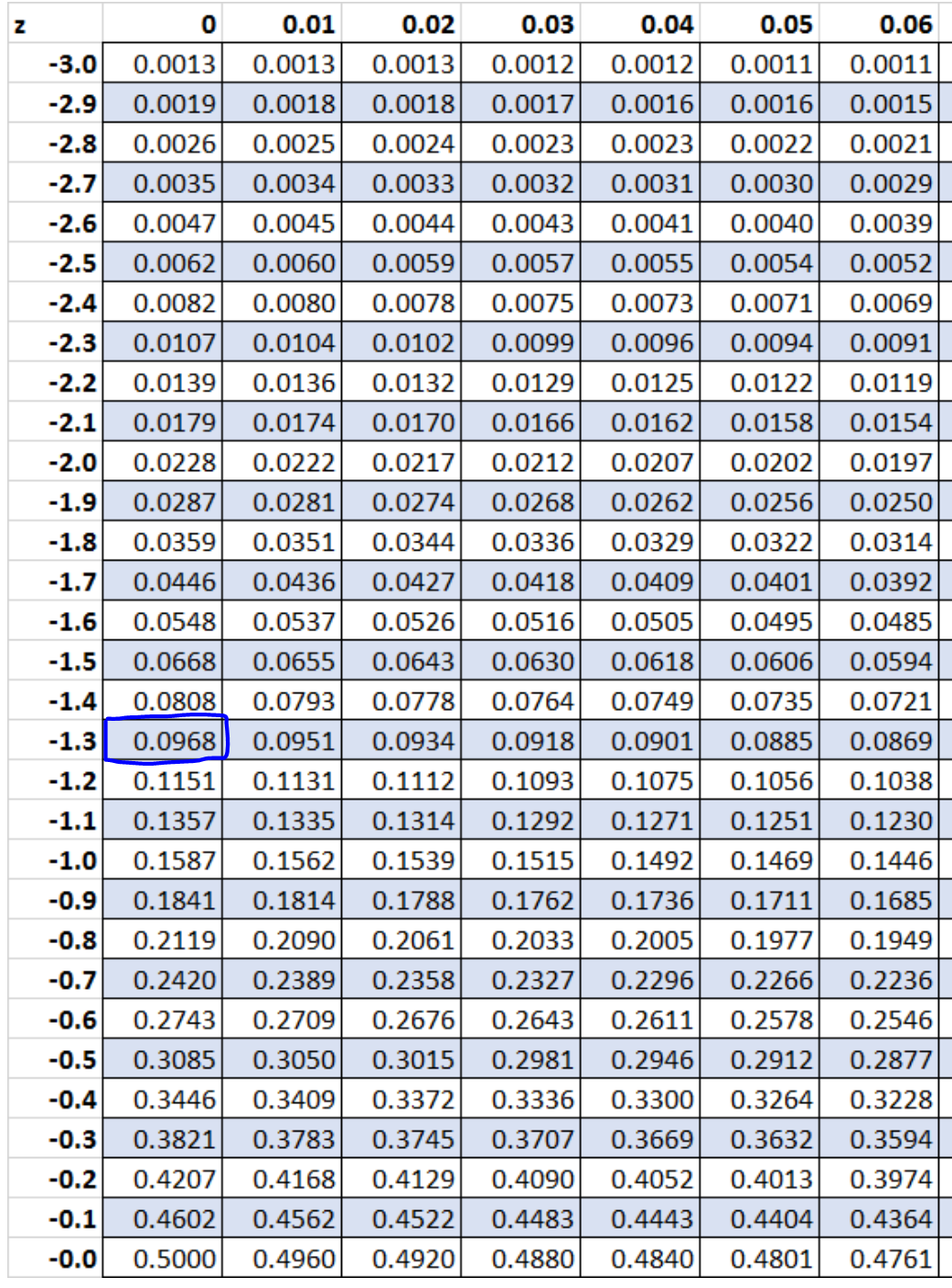
z = (x – μ) / σ = (43.5 – 50) / 5 = -6.5 / 5 = -1.3
ขั้นตอนที่ 5: ใช้ตาราง Z เพื่อค้นหาความน่าจะเป็นที่เกี่ยวข้องกับคะแนน z
ตามตาราง Z ความน่าจะเป็นที่เกี่ยวข้องกับ z = -1.3 คือ 0.0968
ดังนั้นความน่าจะเป็นที่แน่นอนที่เราพบจากการแจกแจงแบบทวินามคือ 0.09667 ในขณะที่ความน่าจะเป็นโดยประมาณที่เราพบโดยใช้การแก้ไขความต่อเนื่องด้วยการแจกแจงแบบปกติคือ 0.0968 สองค่านี้ค่อนข้างปิด
เมื่อใดจึงจะใช้การแก้ไขความต่อเนื่อง
ก่อนที่จะมีซอฟต์แวร์ทางสถิติสมัยใหม่และการคำนวณต้องทำด้วยตนเอง มักใช้การแก้ไขความต่อเนื่องเพื่อค้นหาความน่าจะเป็นที่เกี่ยวข้องกับการแจกแจงแบบไม่ต่อเนื่อง ทุกวันนี้ การแก้ไขความต่อเนื่องมีบทบาทน้อยลงในการคำนวณความน่าจะเป็น เนื่องจากโดยปกติแล้วเราสามารถพึ่งพาซอฟต์แวร์หรือเครื่องคิดเลขเพื่อคำนวณความน่าจะเป็นให้เราได้
แต่เป็นเพียงหัวข้อที่ครอบคลุมในหลักสูตรสถิติเพื่อแสดงความสัมพันธ์ระหว่างการแจกแจงแบบทวินามกับการแจกแจงแบบปกติ และเพื่อแสดงให้เห็นว่าเป็นไปได้ที่การแจกแจงแบบปกติจะประมาณค่าการแจกแจงแบบทวินามโดยใช้การแก้ไขความต่อเนื่อง
เครื่องคิดเลขแก้ไขความต่อเนื่อง
ใช้ เครื่องคำนวณการแก้ไขความต่อเนื่อง เพื่อใช้การแก้ไขความต่อเนื่องกับการแจกแจงแบบปกติกับความน่าจะเป็นแบบทวินามโดยประมาณ