การแจกแจงแบบทวินามลบ

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการแจกแจงแบบทวินามลบคืออะไร และใช้เพื่ออะไร นอกจากนี้ คุณยังจะพบสูตรสำหรับการแจกแจงแบบทวินามลบ ตัวอย่างที่เป็นรูปธรรม และคุณสมบัติของการแจกแจงความน่าจะเป็นประเภทนี้ สุดท้ายนี้ คุณจะสามารถคำนวณความน่าจะเป็นของการแจกแจงแบบทวินามที่เป็นลบด้วยเครื่องคิดเลขออนไลน์ได้

การแจกแจงแบบทวินามลบคืออะไร?

การแจกแจงแบบทวินามที่เป็นลบ คือการแจกแจงความน่าจะเป็นที่อธิบายจำนวนการทดลองเบอร์นูลลีที่จำเป็นเพื่อให้ได้ผลลัพธ์ที่เป็นบวกตามจำนวนที่กำหนด

ดังนั้น การแจกแจงแบบทวินามที่เป็นลบจึงมีพารามิเตอร์ลักษณะเฉพาะ 2 ตัว ได้แก่ r คือจำนวนผลลัพธ์ที่ต้องการ และ p คือความน่าจะเป็นที่จะสำเร็จสำหรับการทดลองเบอร์นูลลีแต่ละครั้ง

$X\sim \text{BN}(r,p)$

โปรดจำไว้ว่าการทดสอบเบอร์นูลลีเป็นการทดลองที่มีผลลัพธ์ที่เป็นไปได้สองแบบ: “ความสำเร็จ” และ “ความล้มเหลว” ดังนั้นหากความน่าจะเป็นของ “ความสำเร็จ” คือ p ความน่าจะเป็นของ “ความล้มเหลว” ก็คือ q=1-p

ดังนั้น การแจกแจงแบบทวินามที่เป็นลบจะกำหนดกระบวนการที่ดำเนินการทดลองเบอร์นูลลีหลายครั้งเท่าที่จำเป็นเพื่อให้ได้ ผลลัพธ์ ที่เป็นบวก นอกจากนี้ การทดลองของ Bernoulli ทั้งหมดนี้มีความเป็นอิสระและมีความน่าจะเป็นที่จะ ประสบความสำเร็จ อย่างต่อเนื่อง

ตัวอย่างเช่น ตัวแปรสุ่มที่ตามหลังการแจกแจงแบบทวินามที่เป็นลบคือจำนวนครั้งที่ต้องทอยลูกเต๋าจนกระทั่งทอยเลข 6 สามครั้ง

ความแตกต่างระหว่างการแจกแจงแบบทวินามที่เป็นลบและการแจกแจงแบบทวินามก็คือ การแจกแจงแบบทวินามเป็นลบจะนับจำนวนครั้งที่ต้องใช้เพื่อให้ได้ผลลัพธ์สำเร็จตามจำนวนที่กำหนด ในขณะที่การแจกแจงแบบทวินามจะนับจำนวนกรณีที่ประสบความสำเร็จในการทดสอบแบบเบอร์นูลลีแบบอนุกรม

➤ ดู: การแจกแจงแบบทวินามคืออะไร?

สูตรการกระจายทวินามลบ

เมื่อพิจารณาจากพารามิเตอร์ r, p, x ความน่าจะเป็นของการแจกแจงแบบทวินามลบจะคำนวณโดยการคูณจำนวนเชิงรวมกันของ x-1 ใน xr ด้วย (1-p) ^xr ด้วย p ^r

ดังนั้น สูตรในการคำนวณความน่าจะเป็นของการแจกแจงแบบทวินามลบ คือ:

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณความน่าจะเป็นของตัวแปรที่ตามหลังการแจกแจงแบบทวินามลบ

แก้แบบฝึกหัดของการแจกแจงแบบทวินามลบ

ความน่าจะเป็นที่ถ้าคุณโยนเหรียญแปดครั้ง เหรียญจะขึ้นหัวครั้งที่สี่ในการโยนครั้งที่แปดเป็นเท่าใด?

ขั้นแรก เราต้องคำนวณความน่าจะเป็นที่จะได้หัวเมื่อโยนเหรียญ ในกรณีนี้ เรามีผลลัพธ์เชิงบวกเพียง 1 รายการ (หัว) จากผลลัพธ์ที่เป็นไปได้ 2 รายการ (หัวและก้อย) ดังนั้นความน่าจะเป็นที่จะประสบความสำเร็จคือ:

$p=\cfrac{1}{2}=0,5$

ดังนั้น ตัวแปรสุ่มในปัญหานี้เป็นไปตามการแจกแจงทวินามลบ โดยที่ r=4 และ p=0.5 ดังนั้นเราจึงใช้สูตรการแจกแจงทวินามลบเพื่อคำนวณความน่าจะเป็นที่แบบฝึกหัดขอให้เราทำ

$\begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}$

ลักษณะของการแจกแจงแบบทวินามลบ

ด้านล่างนี้เป็นคุณลักษณะที่สำคัญที่สุดของการแจกแจงแบบทวินามลบ

การแจกแจงแบบทวินามที่เป็นลบถูกกำหนดโดยพารามิเตอร์ลักษณะเฉพาะสองตัว: r คือจำนวนของผลลัพธ์สำเร็จที่ต้องการ และ p คือความน่าจะเป็นที่จะสำเร็จสำหรับการทดลองเบอร์นูลลีแต่ละครั้งที่ทำ

 *** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.

ความแปรปรวนของการแจกแจงแบบทวินามที่เป็นลบจะเท่ากับ r คูณด้วย (1-p) หารด้วย p ²

$Var(X)=\cfrac{r\cdot (1-p)}{p^2}$

หากพารามิเตอร์ r มากกว่า 1 โหมดของการแจกแจงแบบทวินามลบสามารถคำนวณได้ด้วยสูตรต่อไปนี้:

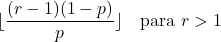
$\displaystyle \lfloor \frac{(r-1)(1-p)}{p}\rfloor\quad \text{para }r>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”221″ style=”vertical-align: -16px;”></p> </p> <ul> <li> ฟังก์ชันมวลซึ่งทำให้สามารถระบุความน่าจะเป็นของการแจกแจงแบบทวินามลบได้ดังต่อไปนี้:</li> </ul> <p class=$ $P[X=x]=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r$

ค่าสัมประสิทธิ์ความเบ้ของการแจกแจงแบบทวินามลบคำนวณได้จากนิพจน์ต่อไปนี้:

$\displaystyle A=\frac{2-p}{\sqrt{r\,(1-p)}}$

ความโด่งของการแจกแจงแบบทวินามลบสามารถพบได้โดยใช้สูตรต่อไปนี้:

$\displaystyle C=\frac{6}{r} + \frac{p^2}{r\,(1-p)}$

หากพารามิเตอร์ r เท่ากับ 1 เราจะมีกรณีของ การแจกแจงทางเรขาคณิต

$r=1 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad X\sim \text{Geometrica}(p)$

เครื่องคำนวณการกระจายทวินามเชิงลบ

ป้อนค่าของพารามิเตอร์ r, p, x ลงในเครื่องคิดเลขต่อไปนี้เพื่อคำนวณความน่าจะเป็น คุณต้องป้อนตัวเลขโดยใช้จุดเป็นตัวคั่นทศนิยม เช่น 0.50

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม