การแจกแจงแบบปกติผกผัน: คำจำกัดความและตัวอย่าง

คำว่า การแจกแจงแบบปกติ ผกผันหมายถึงวิธีการใช้ความน่าจะเป็นที่ทราบเพื่อค้นหาค่าวิกฤต z ที่สอดคล้องกันใน การแจกแจงแบบปกติ

ไม่ควรสับสนกับ การแจกแจงแบบเกาส์เซียนแบบผกผัน ซึ่งเป็นการแจกแจงความน่าจะเป็นแบบต่อเนื่อง

บทช่วยสอนนี้ให้ตัวอย่างหลายประการของการใช้การแจกแจงแบบปกติแบบผกผันในซอฟต์แวร์ทางสถิติต่างๆ

การแจกแจงแบบปกติแบบผกผัน เรามีเครื่องคิดเลข TI-83 หรือ TI-84

คุณมักจะพบคำว่า “การแจกแจงแบบปกติแบบผกผัน” ในเครื่องคิดเลข TI-83 หรือ TI-84 ซึ่งใช้ฟังก์ชันต่อไปนี้เพื่อค้นหาค่าวิกฤต z ที่สอดคล้องกับความน่าจะเป็นบางอย่าง:

invNorm(ความน่าจะเป็น, μ, σ)

ทอง:

• ความน่าจะเป็น: ระดับนัยสำคัญ
• μ: ค่าเฉลี่ยประชากร
• σ: ส่วนเบี่ยงเบนมาตรฐานประชากร

คุณสามารถเข้าถึงฟังก์ชันนี้บนเครื่องคิดเลข TI-84 ได้โดยกด 2 จากนั้นกด vars สิ่งนี้จะนำคุณไปยังหน้าจอ DISTR ซึ่งคุณสามารถใช้ invNorm() :

ตัวอย่างเช่น เราสามารถใช้ฟังก์ชันนี้เพื่อค้นหาค่าวิกฤต z ที่สอดคล้องกับค่าความน่าจะเป็น 0.05:

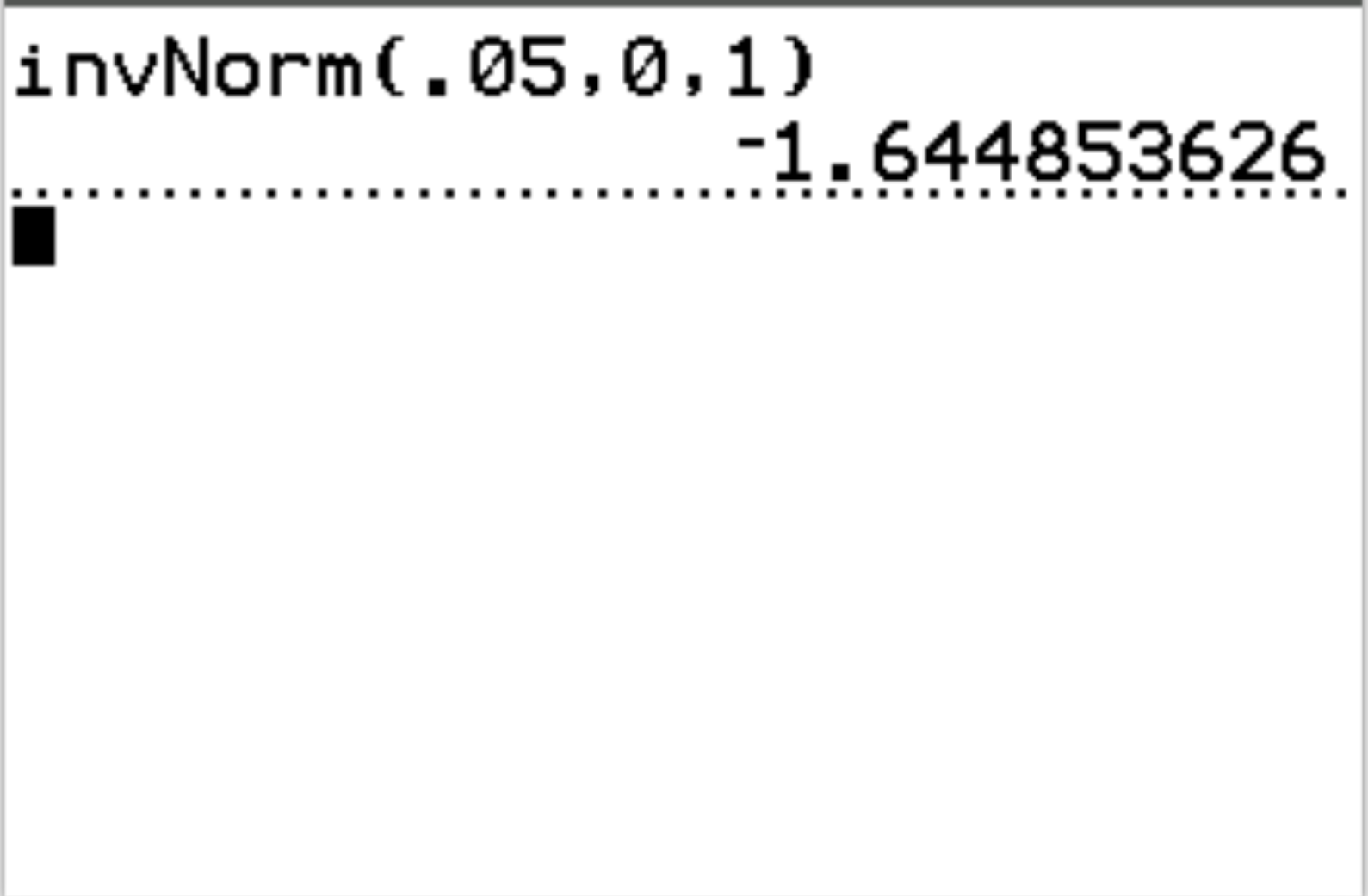
ค่าวิกฤต z ที่สอดคล้องกับค่าความน่าจะเป็น 0.05 คือ -1.64485

ที่เกี่ยวข้อง: วิธีใช้ invNorm บนเครื่องคิดเลข TI-84 (พร้อมตัวอย่าง)

การแจกแจงแบบปกติผกผันใน Excel

เมื่อต้องการค้นหาค่าวิกฤต z ที่เกี่ยวข้องกับค่าความน่าจะเป็นใน Excel เราสามารถใช้ฟังก์ชัน INVNORM() ซึ่งใช้ไวยากรณ์ต่อไปนี้:

INVNORM(p, ค่าเฉลี่ย, sd)

ทอง:

• p: ระดับความสำคัญ
• เฉลี่ย: ค่าเฉลี่ยประชากร
• sd: ส่วนเบี่ยงเบนมาตรฐานประชากร

ตัวอย่างเช่น เราสามารถใช้ฟังก์ชันนี้เพื่อค้นหาค่าวิกฤต z ที่สอดคล้องกับค่าความน่าจะเป็น 0.05:

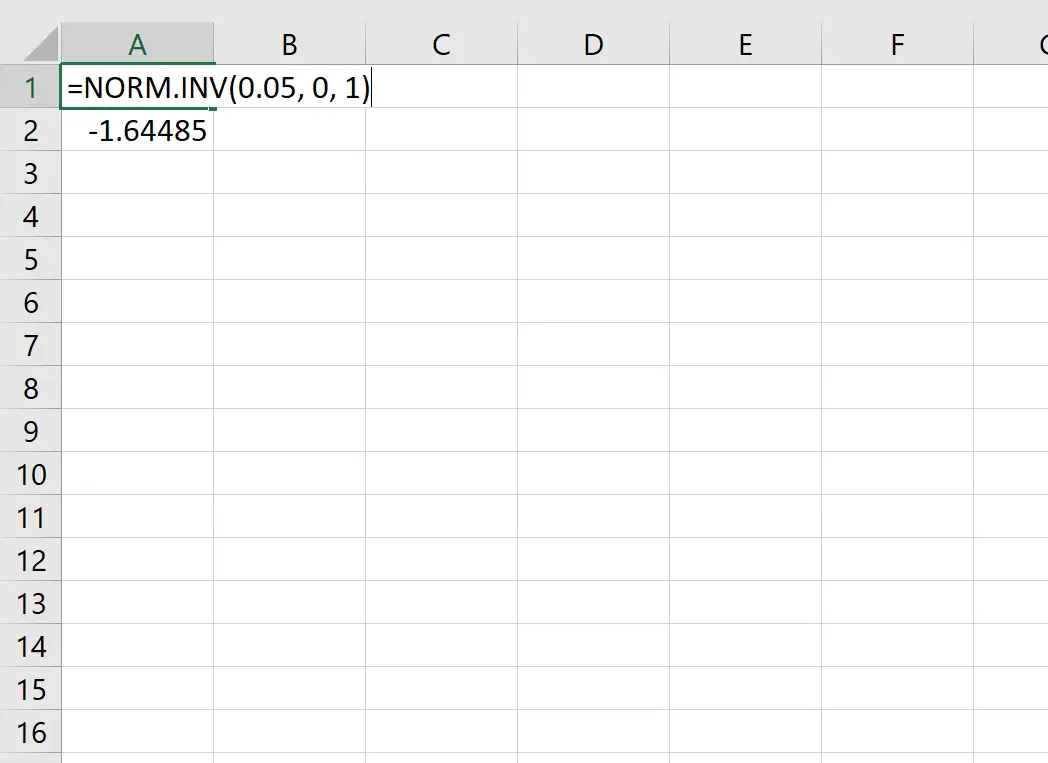
ค่าวิกฤต z ที่สอดคล้องกับค่าความน่าจะเป็น 0.05 คือ -1.64485

การแจกแจงแบบปกติผกผันใน R

หากต้องการค้นหาค่าวิกฤต z ที่เกี่ยวข้องกับค่าความน่าจะเป็นใน R เราสามารถใช้ฟังก์ชัน qnorm() ซึ่งใช้ไวยากรณ์ต่อไปนี้:

qnorm (p, ค่าเฉลี่ย, sd)

ทอง:

• p: ระดับความสำคัญ
• เฉลี่ย: ค่าเฉลี่ยประชากร
• sd: ส่วนเบี่ยงเบนมาตรฐานประชากร

ตัวอย่างเช่น เราสามารถใช้ฟังก์ชันนี้เพื่อค้นหาค่าวิกฤต z ที่สอดคล้องกับค่าความน่าจะเป็น 0.05:

 qnorm (p= .05 , mean= 0 , sd= 1 )

[1] -1.644854

ขอย้ำอีกครั้งว่าค่า z วิกฤตที่สอดคล้องกับค่าความน่าจะเป็น 0.05 คือ -1.64485