การแจกแจงแบบปกติและการแจกแจงแบบ t: อะไรคือความแตกต่าง?

การแจกแจงแบบปกติ คือการแจกแจงที่ใช้กันมากที่สุดในสถิติทั้งหมด และเป็นที่รู้กันว่าเป็นการแจกแจงแบบสมมาตรและเป็นรูปทรงระฆัง

การกระจายที่เกี่ยวข้องกันอย่างใกล้ชิดคือ การแจกแจงแบบ t ซึ่งมีลักษณะสมมาตรและมีรูปทรงระฆังเช่นกัน แต่มี “หาง” ที่หนักกว่าการกระจายแบบปกติ

กล่าวอีกนัยหนึ่ง ค่ามากกว่าในการแจกแจงจะอยู่ที่ส่วนท้ายมากกว่าตรงกลางเมื่อเทียบกับการแจกแจงแบบปกติ:

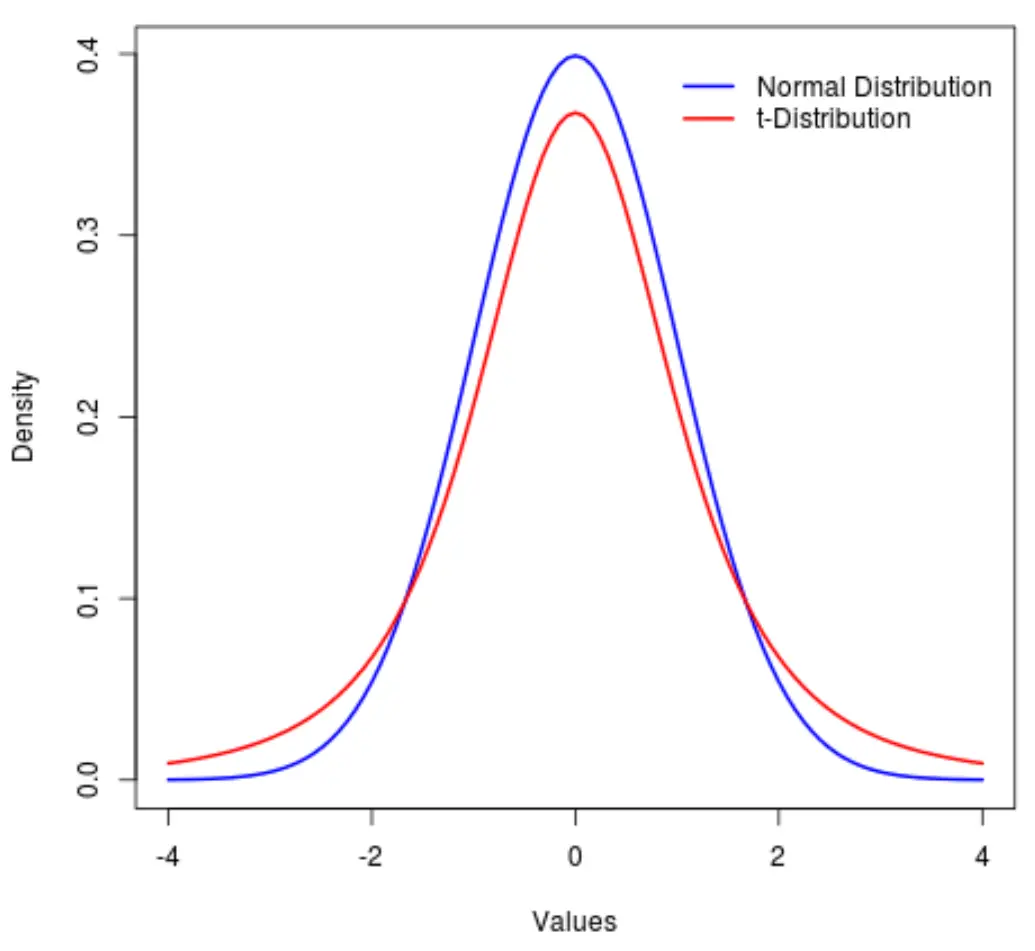
ในศัพท์แสงทางสถิติ เราใช้หน่วยเมตริกที่เรียกว่า เคอร์โทซิส เพื่อวัดว่าการกระจายนั้น “หนัก” เพียงใด ดังนั้น เราจะบอกว่าความโด่งของการแจกแจงแบบ t นั้นมากกว่าการแจกแจงแบบปกติ

ในทางปฏิบัติ เรามักใช้การแจกแจงแบบ t เมื่อทำการ ทดสอบสมมติฐาน หรือ สร้างช่วงความเชื่อมั่น

ตัวอย่างเช่น สูตรในการคำนวณช่วงความเชื่อมั่นสำหรับค่าเฉลี่ยประชากรคือ:

ช่วงความเชื่อมั่น = x +/- t _{1-α/2, n-1} *(s/√ n )

ทอง:

• x : ค่าเฉลี่ยตัวอย่าง
• t: ค่าวิกฤต t ซึ่งขึ้นอยู่กับระดับนัยสำคัญ α และขนาดตัวอย่าง n
• s: ค่าเบี่ยงเบนมาตรฐานตัวอย่าง
• n: ขนาดตัวอย่าง

ในสูตรนี้ เราใช้ค่าวิกฤตของตาราง t แทนค่าวิกฤตของตาราง z เมื่อเงื่อนไขข้อใดข้อหนึ่งต่อไปนี้เป็นจริง:

• เราไม่รู้ค่าเบี่ยงเบนมาตรฐานประชากร
• ขนาดตัวอย่างน้อยกว่าหรือเท่ากับ 30

ผังงานต่อไปนี้ให้วิธีที่เป็นประโยชน์ในการทราบว่าคุณควรใช้ค่าวิกฤตจากตาราง t หรือตาราง z:

ข้อแตกต่างที่สำคัญระหว่างการใช้การแจกแจงแบบ t และการใช้การแจกแจงแบบปกติเมื่อสร้างช่วงความเชื่อมั่นก็คือ ค่าวิกฤตของการแจกแจงแบบ t จะมีขนาดใหญ่ขึ้น นำไปสู่ช่วงความเชื่อมั่น ที่กว้างขึ้น

ตัวอย่างเช่น สมมติว่าเราต้องการสร้างช่วงความเชื่อมั่น 95% สำหรับน้ำหนักเฉลี่ยของประชากรเต่า เพื่อสุ่มตัวอย่างเต่าโดยมีข้อมูลต่อไปนี้:

• ขนาดตัวอย่าง n = 25
• น้ำหนักตัวอย่างเฉลี่ย x = 300
• ตัวอย่างค่าเบี่ยงเบนมาตรฐาน s = 18.5

ค่า z วิกฤตสำหรับระดับความเชื่อมั่น 95% คือ 1.96 ในขณะที่ค่า t วิกฤตสำหรับช่วงความเชื่อมั่น 95% โดยที่ df = 25-1 = 24 องศาอิสระคือ 2.0639

ดังนั้น ช่วงความเชื่อมั่น 95% สำหรับค่าเฉลี่ยประชากรที่ใช้ค่าวิกฤต z คือ:

CI 95% = 300 +/- 1.96*(18.5/√ 25 ) = [292.75, 307.25]

ในขณะที่ช่วงความเชื่อมั่น 95% สำหรับค่าเฉลี่ยประชากรที่ใช้ค่า t-critical คือ:

CI 95% = 300 +/- 2.0639*(18.5/√25) = [292.36, 307.64]

โปรดทราบว่าช่วงความเชื่อมั่นที่มีค่า t-critical นั้นกว้างกว่า

แนวคิดนี้คือเมื่อเรามีขนาดตัวอย่างน้อย เราจะไม่แน่ใจในค่าเฉลี่ยประชากรที่แท้จริง ดังนั้นจึงเป็นประโยชน์ที่จะใช้การแจกแจงแบบ t เพื่อสร้างช่วงความเชื่อมั่นที่กว้างขึ้นซึ่งมีโอกาสมากขึ้นที่จะมีค่าเฉลี่ยประชากรที่แท้จริง

การแสดงดีกรีอิสระสำหรับการแจกแจงแบบ t

ควรสังเกตว่าเมื่อระดับความเป็นอิสระเพิ่มขึ้น การแจกแจงแบบ t จะเข้าใกล้การแจกแจงแบบปกติ

เพื่ออธิบายสิ่งนี้ ให้พิจารณากราฟต่อไปนี้ซึ่งแสดงรูปร่างของการแจกแจงแบบ t โดยมีดีกรีอิสระดังต่อไปนี้:

• ดีเอฟ = 3
• ดีเอฟ = 10
• df = 30

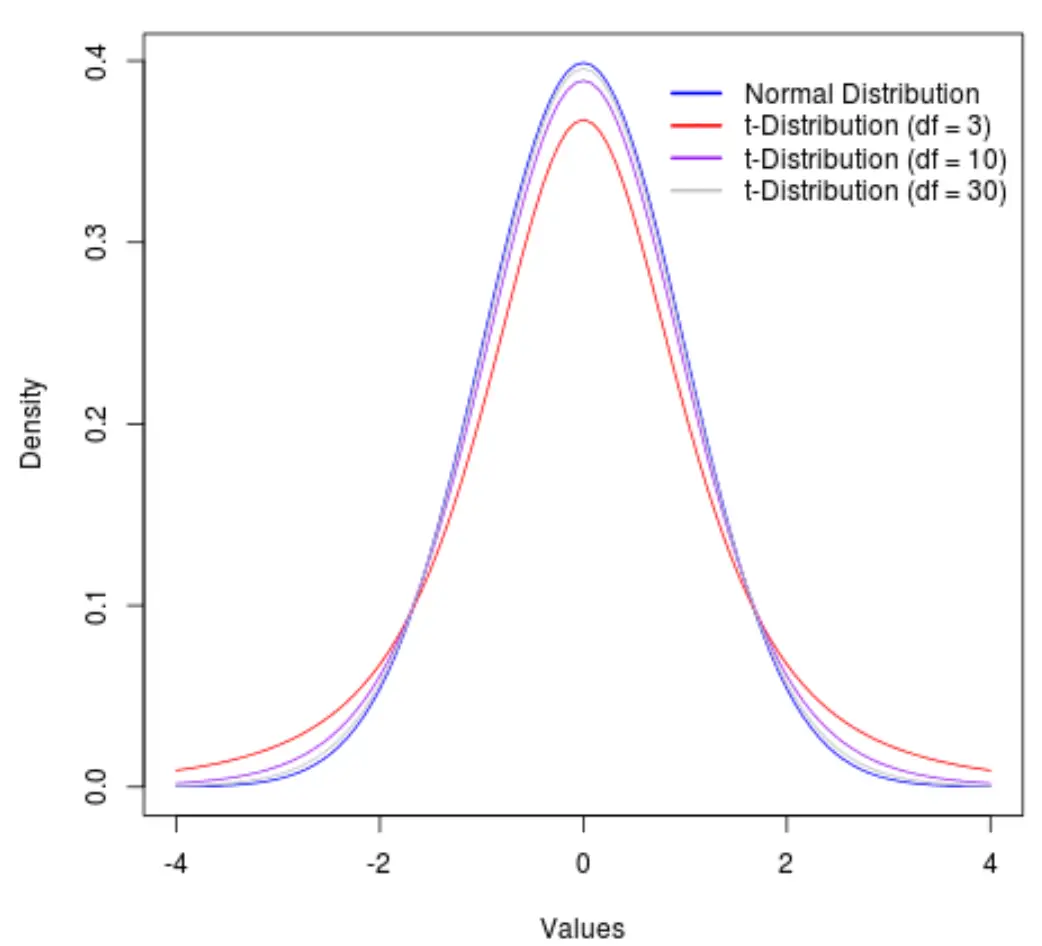
เมื่อเกิน 30 องศาของความเป็นอิสระ การแจกแจงแบบ t และการแจกแจงแบบปกติจะคล้ายกันมากจนความแตกต่างระหว่างการใช้ค่าวิกฤต t และค่าวิกฤติ z ในสูตรจะน้อยมาก