การกระจายแบบเอ็กซ์โปเนนเชียล

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าการแจกแจงแบบเอ็กซ์โปเนนเชียลในสถิติคืออะไร และใช้เพื่ออะไร ในทำนองเดียวกัน คุณจะพบคุณสมบัติของการแจกแจงแบบเอ็กซ์โปเนนเชียล รวมถึงสูตร กราฟ และแบบฝึกหัดที่แก้ไขได้ นอกจากนี้ คุณจะสามารถคำนวณความน่าจะเป็นได้ด้วยเครื่องคำนวณการแจกแจงแบบเอ็กซ์โพเนนเชียลแบบออนไลน์

การกระจายแบบเอ็กซ์โปเนนเชียลคืออะไร?

การแจกแจงแบบเอกซ์โปเนนเชียล เป็นการแจกแจงความน่าจะเป็นแบบต่อเนื่องที่ใช้ในการจำลองเวลารอคอยให้เกิดปรากฏการณ์สุ่ม

แม่นยำยิ่งขึ้น การแจกแจงแบบเอกซ์โปเนนเชียลช่วยให้เราสามารถอธิบายเวลาที่รอคอยระหว่างสองเหตุการณ์ที่ตามหลังการแจกแจงแบบปัวซอง ดังนั้นการแจกแจงแบบเอ็กซ์โปเนนเชียลจึงสัมพันธ์อย่างใกล้ชิดกับการแจกแจงแบบปัวซอง

➤ ดู: การแจกแจงแบบปัวซองคืออะไร

การแจกแจงแบบเอกซ์โปเนนเชียลมีพารามิเตอร์ลักษณะเฉพาะ แสดงด้วยตัวอักษรกรีก γ และระบุจำนวนครั้งที่เหตุการณ์ที่ศึกษาคาดว่าจะเกิดขึ้นในช่วงเวลาที่กำหนด

$X\sim \text{Exp}(\lambda)$

ในทำนองเดียวกัน การแจกแจงแบบเอกซ์โพเนนเชียลยังใช้ในการจำลองเวลาจนกระทั่งเกิดความล้มเหลวอีกด้วย การแจกแจงแบบเอ็กซ์โปเนนเชียลจึงนำไปประยุกต์ใช้หลายประการในทฤษฎีความน่าเชื่อถือและการอยู่รอด

ตัวอย่างของการแจกแจงแบบเอ็กซ์โปเนนเชียล

ตอนนี้เรารู้คำจำกัดความของการแจกแจงแบบเอ็กซ์โปเนนเชียลแล้ว เรามาดูตัวอย่างต่างๆ ของการแจกแจงประเภทนี้เพื่อทำความเข้าใจแนวคิดนี้กันดีกว่า

ตัวอย่างของการแจกแจงแบบเอ็กซ์โปเนนเชียล:

เวลาที่ผ่านไประหว่างการโทรสองครั้งในศูนย์บริการทางโทรศัพท์
เวลาที่บุคคลต้องรอจนกว่ารถแท็กซี่ฟรีจะผ่านไปบนถนนสายหนึ่งโดยเฉพาะ
ระยะเวลารอจนกว่าลูกค้าใหม่จะเข้าร้าน
เวลาที่ผ่านไประหว่างผู้ใช้สองคนที่เข้าสู่หน้าเว็บ
เวลาที่ผ่านไปที่สนามบินแห่งหนึ่งระหว่างเครื่องขึ้นและออกอีกเครื่องหนึ่ง

สูตรการกระจายแบบเอ็กซ์โปเนนเชียล

สูตรฟังก์ชันความหนาแน่นที่กำหนดการคำนวณความน่าจะเป็นของการแจกแจงแบบเอกซ์โปเนนเชียลจะเท่ากับ lam คูณด้วยจำนวน e กำลังของลบ lam คูณ x

กล่าวอีกนัยหนึ่ง สูตรในการคำนวณความน่าจะเป็นของการแจกแจงแบบเลขชี้กำลัง มีดังนี้

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างนี้เพื่อคำนวณความน่าจะเป็นของตัวแปรที่ตามหลังการแจกแจงแบบเอ็กซ์โปเนนเชียล

ในทางกลับกัน สูตรคำนวณความน่าจะเป็นสะสมของการแจกแจงแบบเลขชี้กำลังมีดังนี้

$P[X\leq x]=1-e^{-\lambda x}$

กราฟการกระจายแบบเอ็กซ์โปเนนเชียล

ในส่วนนี้ คุณจะเห็นการแสดงฟังก์ชันความหนาแน่นและฟังก์ชันการกระจายของการแจกแจงแบบเอ็กซ์โปเนนเชียลในรูปแบบกราฟิก

ด้านล่างนี้ คุณจะเห็นว่ากราฟของฟังก์ชันความหนาแน่นของการแจกแจงแบบเอ็กซ์โปเนนเชียลแตกต่างกันอย่างไร โดยขึ้นอยู่กับค่าของพารามิเตอร์ γ

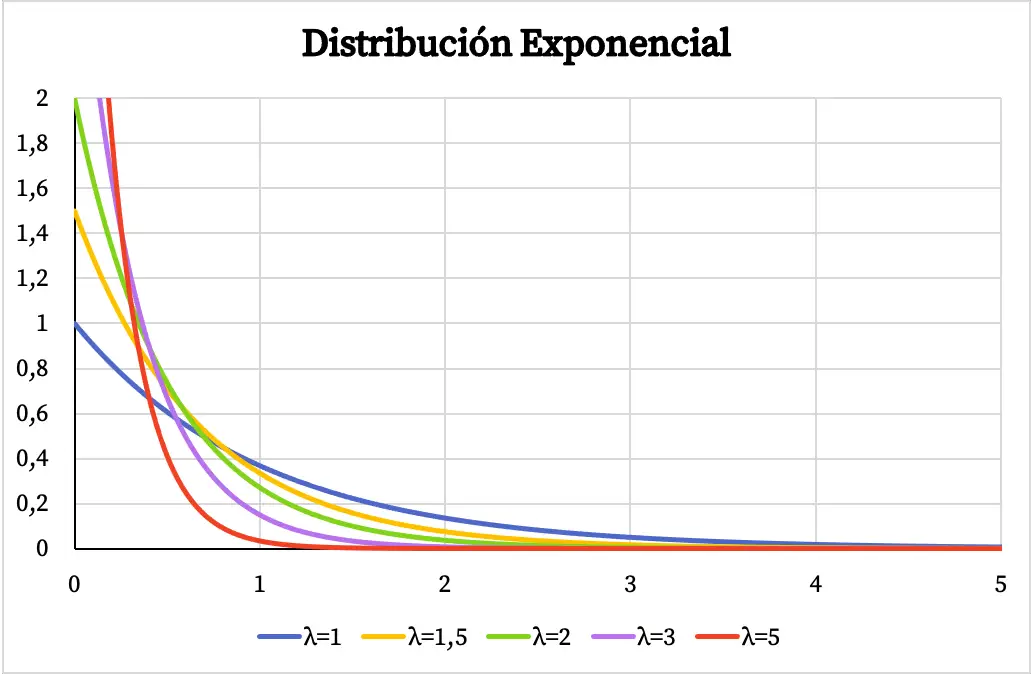
ในทำนองเดียวกัน ฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบเอ็กซ์โปเนนเชียลยังขึ้นอยู่กับค่าของพารามิเตอร์ γ ดังที่คุณเห็นในกราฟต่อไปนี้:

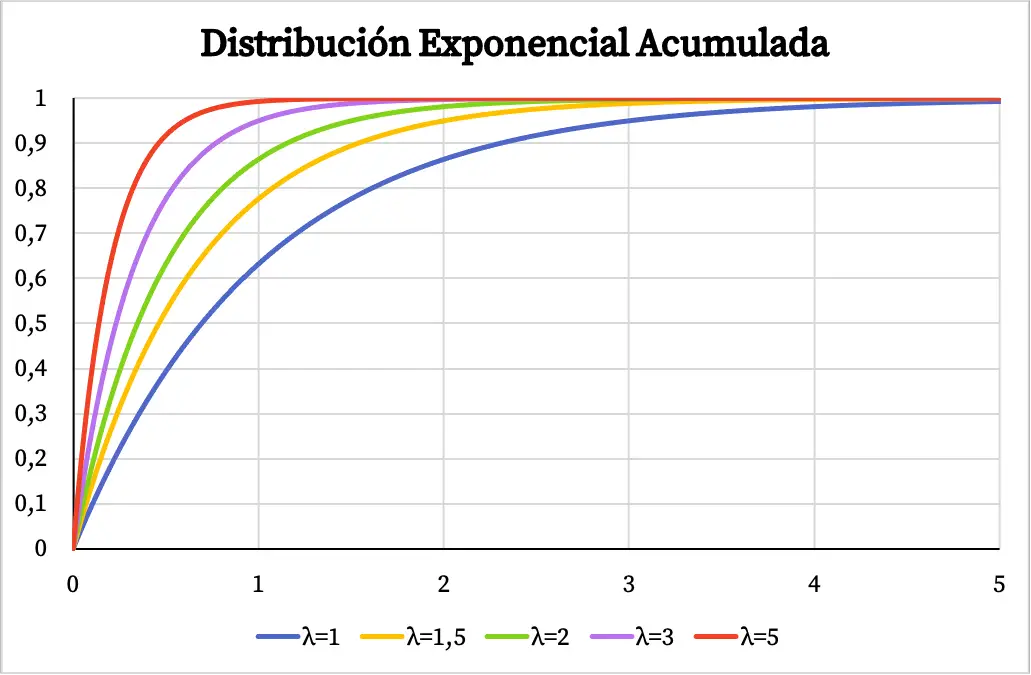
กราฟความน่าจะเป็นของการแจกแจงแบบเอ็กซ์โปเนนเชียลสะสม

แก้แบบฝึกหัดเรื่องการแจกแจงแบบเอ็กซ์โปเนนเชียล

โดยเฉลี่ย แล = 1 ผู้ใช้/นาที เข้าถึงหน้าเว็บที่ต้องการ ความน่าจะเป็นที่เวลาระหว่างผู้ใช้สองคนเข้าคือ 3 นาทีเป็นเท่าใด และความน่าจะเป็นที่จะเท่ากับหรือน้อยกว่า 2 นาที?

การแจกแจงที่กำหนดตัวแปรสุ่มของปัญหานี้คือการแจกแจงแบบเอ็กซ์โพเนนเชียล เนื่องจากเราศึกษาเวลาที่ผ่านไปจากช่วงเวลาที่เหตุการณ์เกิดขึ้น (การเข้ามาของผู้ใช้บนหน้าเว็บ) จนกระทั่งเหตุการณ์เดียวกันนี้เกิดขึ้นอีกครั้ง

$X\sim \text{Exp}(1)$

ดังนั้น ในการคำนวณความน่าจะเป็นที่เวลาที่ผ่านไประหว่างรายการของผู้ใช้สองคนที่แตกต่างกันคือสามนาที เราจำเป็นต้องใช้สูตรฟังก์ชันความหนาแน่น (ดูด้านบน):

$\begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}$

ในทางกลับกัน เพื่อพิจารณาความน่าจะเป็นสะสม เราต้องใช้สูตรฟังก์ชันการแจกแจงของการแจกแจงแบบเลขชี้กำลัง:

$\begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}$

ลักษณะของการแจกแจงแบบเอ็กซ์โปเนนเชียล

การแจกแจงแบบเอ็กซ์โปเนนเชียลมีลักษณะดังต่อไปนี้:

การแจกแจงแบบเอ็กซ์โพเนนเชียลมีพารามิเตอร์ลักษณะเฉพาะ แล ซึ่งระบุจำนวนครั้งที่ปรากฏการณ์ที่ศึกษาคาดว่าจะเกิดขึ้นในช่วงเวลาที่กำหนด

$X\sim \text{Exp}(\lambda)$

การแจกแจงแบบเอ็กซ์โปเนนเชียลไม่สามารถรับค่าลบได้ ดังนั้นโดเมนของการแจกแจงแบบเอ็กซ์โปเนนเชียลจึงประกอบด้วยจำนวนจริงทั้งหมดที่มากกว่าหรือเท่ากับศูนย์

$x\in [0,+\infty)$

ค่าเฉลี่ยของการแจกแจงแบบเอ็กซ์โพเนนเชียลเท่ากับหนึ่งหารด้วยพารามิเตอร์ลักษณะเฉพาะ แล

$E[X]=\cfrac{1}{\lambda}$

ความแปรปรวนของการแจกแจงแบบเอ็กซ์โปเนนเชียลคือกำลังสองของค่าเฉลี่ย ดังนั้นความแปรปรวนของการแจกแจงแบบเอ็กซ์โปเนนเชียลจึงเท่ากับ 1 ส่วนสัมประสิทธิ์ แลมพาร์ดกำลังสอง

$Var(X)=\cfrac{1}{\lambda^2 }$

ไม่ว่าค่าของ แล จะเป็นอย่างไร ค่าสัมประสิทธิ์ความไม่สมมาตรของการแจกแจงแบบเอ็กซ์โปเนนเชียลจะเท่ากับ 2 เสมอ

$A=2$

ในทำนองเดียวกัน ค่าสัมประสิทธิ์ความโด่งของการแจกแจงแบบเอ็กซ์โปเนนเชียลจะเท่ากับ 9 เสมอ

$C=9$

สูตรสำหรับฟังก์ชันความหนาแน่นของการแจกแจงแบบเลขชี้กำลังคือ:

$P[X=x]=\lambda e^{-\lambda x}$

ในขณะที่สูตรสำหรับฟังก์ชันความน่าจะเป็นสะสมของการแจกแจงแบบเลขชี้กำลังมีดังนี้

$P[X\leq x]=1-e^{-\lambda x}$

การแจกแจงแบบเอ็กซ์โปเนนเชียลเป็นหนึ่งในการแจกแจงความน่าจะเป็นไม่กี่แบบที่มีคุณสมบัติหน่วยความจำไม่เพียงพอ คุณสมบัตินี้หมายความว่าการเกิดขึ้นของเหตุการณ์ก่อนหน้าไม่ส่งผลกระทบต่อความน่าจะเป็นของเหตุการณ์นั้นที่จะเกิดขึ้นในอนาคต ตัวอย่างเช่น ในการแจกแจงแบบเอ็กซ์โพเนนเชียล ความน่าจะเป็นที่ผู้ใช้ใหม่จะเข้าถึงหน้าเว็บภายในเวลาไม่ถึงนาทีไม่ได้ขึ้นอยู่กับว่าผู้ใช้เพิ่งป้อนหรือไม่มีผู้ใช้เลยตั้งแต่นั้นมา มากกว่าสิบนาที

$P[X>x+y|X>y]=P[X>x]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”254″ style=”vertical-align: -5px;”></p> </p> <h2 class=$ เครื่องคำนวณการกระจายแบบเอ็กซ์โปเนนเชียล

ป้อนค่าของพารามิเตอร์ แลม และค่าของ x ลงในเครื่องคิดเลขต่อไปนี้เพื่อคำนวณความน่าจะเป็น คุณต้องเลือกความน่าจะเป็นที่คุณต้องการคำนวณและป้อนตัวเลขโดยใช้จุดเป็นตัวคั่นทศนิยม เช่น 0.50

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม