ขนาดเอฟเฟกต์: คืออะไรและเหตุใดจึงสำคัญ
“นัยสำคัญทางสถิติคือสิ่งที่น่าสนใจน้อยที่สุดเกี่ยวกับผลลัพธ์ คุณต้องอธิบายผลลัพธ์ในแง่ของขนาด – ไม่เพียงแต่การรักษาส่งผลกระทบต่อผู้คน แต่ยังส่งผลต่อพวกเขามากน้อยเพียงใด -ยีน วี.กลาส
ในเชิงสถิติ เรามักจะใช้ ค่า p เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างสองกลุ่มหรือไม่
ตัวอย่างเช่น สมมติว่าเราต้องการทราบว่าเทคนิคการศึกษาสองแบบที่แตกต่างกันนำไปสู่คะแนนการทดสอบที่แตกต่างกันหรือไม่ ดังนั้นเราจึงมีนักเรียนกลุ่มละ 20 คนที่ใช้เทคนิคการเรียนแบบหนึ่งเพื่อเตรียมตัวสำหรับการทดสอบ ในขณะที่นักเรียนอีกกลุ่มจำนวน 20 คนใช้เทคนิคการเรียนที่แตกต่างกัน จากนั้นเราจะให้นักเรียนแต่ละคนทำแบบทดสอบเดียวกัน
หลังจากทำการทดสอบทีสองตัวอย่างเพื่อหาความแตกต่างในค่าเฉลี่ย เราพบว่าค่า p สำหรับการทดสอบคือ 0.001 หากเราใช้ระดับนัยสำคัญที่ 0.05 หมายความว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างผลลัพธ์เฉลี่ยของทั้งสองกลุ่ม ดังนั้นเทคนิคการเรียนจึงส่งผลต่อผลการทดสอบ
อย่างไรก็ตาม แม้ว่าค่า p-value จะบอกเราว่าเทคนิคการเรียนรู้มีผลกระทบต่อคะแนนการทดสอบ แต่ก็ไม่ได้บอกเรา ถึงขนาด ของผลกระทบนั้น เพื่อให้เข้าใจสิ่งนี้ เราจำเป็นต้องทราบ ขนาดเอฟเฟกต์
ขนาดเอฟเฟกต์คืออะไร?
ขนาดเอฟเฟกต์ เป็นวิธีหาปริมาณความแตกต่างระหว่างสองกลุ่ม
แม้ว่าค่า p จะบอกเราได้ว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างสองกลุ่มหรือไม่ แต่ขนาดของเอฟเฟกต์สามารถบอกเราได้ว่าจริงๆ แล้วความแตกต่างนั้น ใหญ่แค่ไหน ในทางปฏิบัติ ขนาดเอฟเฟกต์มีความน่าสนใจและมีประโยชน์มากกว่าค่า p มาก
มีสามวิธีในการวัดขนาดเอฟเฟกต์ ขึ้นอยู่กับประเภทของการวิเคราะห์ที่คุณกำลังทำ:
1. ผลต่างค่าเฉลี่ยที่ได้มาตรฐาน
เมื่อคุณต้องการศึกษาความแตกต่างเฉลี่ยระหว่างสองกลุ่ม วิธีที่เหมาะสมในการคำนวณขนาดเอฟเฟกต์คือการใช้ ผลต่างเฉลี่ยที่เป็นมาตรฐาน สูตรที่นิยมใช้กันมากที่สุดเรียกว่า Cohen’s d ซึ่งคำนวณได้ดังนี้
D ของ โคเฮน = ( x1 – x2 )/ วินาที
โดยที่ x 1 และ x 2 เป็นค่าเฉลี่ยตัวอย่างของกลุ่ม 1 และกลุ่ม 2 ตามลำดับ และ s คือค่าเบี่ยงเบนมาตรฐานของประชากรที่ดึงทั้งสองกลุ่มมา
เมื่อใช้สูตรนี้ ขนาดของเอฟเฟกต์จะตีความได้ง่าย:
- d ของ 1 บ่งชี้ว่าค่าเฉลี่ยของทั้งสองกลุ่มต่างกันด้วยค่าเบี่ยงเบนมาตรฐานหนึ่งค่า
- d ของ 2 หมายความว่าค่าเฉลี่ยของกลุ่มต่างกันด้วยค่าเบี่ยงเบนมาตรฐาน 2 ค่า
- ค่า d ของ 2.5 บ่งชี้ว่าค่าเฉลี่ยทั้งสองต่างกันด้วยค่าเบี่ยงเบนมาตรฐาน 2.5 และอื่นๆ
วิธีตีความขนาดเอฟเฟกต์อีกวิธีหนึ่งคือ ขนาดเอฟเฟกต์ 0.3 หมายความว่าคะแนนของบุคคลโดยเฉลี่ยในกลุ่ม 2 มีค่าเบี่ยงเบนมาตรฐาน 0.3 ซึ่งสูงกว่าค่าเฉลี่ยบุคคลของกลุ่ม 1 และจึงเกินคะแนน 62% ของกลุ่ม 1 .
ตารางต่อไปนี้แสดงขนาดเอฟเฟกต์ที่แตกต่างกันและเปอร์เซ็นไทล์ที่สอดคล้องกัน:
| ขนาดเอฟเฟกต์ | เปอร์เซ็นต์ของกลุ่ม ที่ 2 ซึ่งจะต่ำกว่าค่าเฉลี่ยของคนในกลุ่มที่ 1 |
|---|---|
| 0.0 | 50% |
| 0.2 | 58% |
| 0.4 | 66% |
| 0.6 | 73% |
| 0.8 | 79% |
| 1.0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1.8 | 96% |
| 2.0 | 98% |
| 2.5 | 99% |
| 3.0 | 99.9% |
ยิ่งขนาดเอฟเฟกต์ใหญ่ขึ้น ความแตกต่างระหว่างบุคคลโดยเฉลี่ยในแต่ละกลุ่มก็จะยิ่งมากขึ้นเท่านั้น
โดยทั่วไป d 0.2 หรือน้อยกว่าถือเป็นขนาดเอฟเฟกต์ขนาดเล็ก d ประมาณ 0.5 ถือเป็นขนาดเอฟเฟกต์ปานกลาง และ d 0.8 หรือมากกว่านั้นถือเป็นขนาดเอฟเฟกต์ขนาดใหญ่
ดังนั้น หากค่าเฉลี่ยของทั้งสองกลุ่มไม่แตกต่างกันอย่างน้อย 0.2 ส่วนเบี่ยงเบนมาตรฐาน ความแตกต่างก็ไม่มีนัยสำคัญ แม้ว่าค่า p จะมีนัยสำคัญทางสถิติก็ตาม
2. ค่าสัมประสิทธิ์สหสัมพันธ์
เมื่อคุณต้องการศึกษาความสัมพันธ์เชิงปริมาณระหว่างตัวแปรสองตัว วิธีที่ใช้กันทั่วไปในการคำนวณขนาดเอฟเฟกต์คือใช้ สัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน เป็นการวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปร X และ Y สองตัว โดยมีค่าระหว่าง -1 ถึง 1 โดยที่:
- -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
- 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
- 1 บ่งชี้ความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
สูตรการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันค่อนข้างซับซ้อน แต่สำหรับผู้ที่สนใจสามารถพบได้ ที่นี่
ยิ่งค่าสัมประสิทธิ์สหสัมพันธ์จากศูนย์มากเท่าใด ความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัวก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น สิ่งนี้สามารถเห็นได้ด้วยการสร้างแผนภาพกระจายอย่างง่ายของค่าของตัวแปร X และ Y
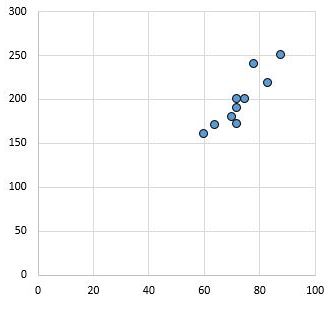
ตัวอย่างเช่น แผนภาพกระจายต่อไปนี้จะแสดงค่าของตัวแปรสองตัวที่มีค่าสัมประสิทธิ์สหสัมพันธ์เท่ากับ r = 0.94
ค่านี้อยู่ไกลจากศูนย์ ซึ่งบ่งชี้ว่ามีความสัมพันธ์เชิงบวกที่แข็งแกร่งระหว่างตัวแปรทั้งสอง
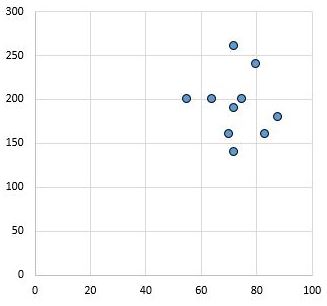
ในทางกลับกัน Scatterplot ต่อไปนี้จะแสดงค่าของตัวแปรสองตัวที่มีค่าสัมประสิทธิ์สหสัมพันธ์ r = 0.03 ค่านี้ใกล้กับศูนย์ ซึ่งบ่งชี้ว่าแทบไม่มีความสัมพันธ์กันระหว่างตัวแปรทั้งสอง
โดยทั่วไป ขนาดเอฟเฟกต์จะถือว่าน้อยหากค่าของสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน r อยู่ที่ประมาณ 0.1 ค่าปานกลางหาก r อยู่ที่ประมาณ 0.3 และมีขนาดใหญ่หาก r เท่ากับหรือมากกว่า 0.5
3. อัตราต่อรอง
เมื่อคุณต้องการศึกษาโอกาสที่จะประสบความสำเร็จในกลุ่มการรักษาเทียบกับโอกาสที่จะประสบความสำเร็จในกลุ่มควบคุม วิธีที่ใช้กันทั่วไปในการคำนวณขนาดผลลัพธ์คือการใช้ อัตราส่วนอัตราต่อรอง
ตัวอย่างเช่น สมมติว่าเรามีตารางต่อไปนี้:
| ขนาดเอฟเฟกต์ | #ความสำเร็จ | # หมากรุก |
|---|---|---|
| กลุ่มบำบัด | มี | บี |
| กลุ่มควบคุม | VS | ดี |
อัตราต่อรองจะถูกคำนวณดังนี้:
อัตราต่อรอง = (AD) / (BC)
ยิ่งอัตราส่วนอัตราต่อรองอยู่ที่ 1 มากเท่าใด ความน่าจะเป็นที่การรักษาจะได้ผลจริงก็จะยิ่งสูงขึ้นเท่านั้น
ประโยชน์ของการใช้ขนาดเอฟเฟกต์เหนือค่า P
ขนาดเอฟเฟกต์มีข้อดีมากกว่าค่า p หลายประการ:
1. ขนาดเอฟเฟกต์ช่วยให้เราเข้าใจได้ดีขึ้นว่าความแตกต่างระหว่างสองกลุ่มนั้น ใหญ่แค่ไหน หรือความสัมพันธ์ระหว่างสองกลุ่มนั้น แข็งแกร่งแค่ไหน ค่า p สามารถบอกเราได้เพียงว่า มี ความแตกต่างที่มีนัยสำคัญหรือมีความสัมพันธ์กันที่มีนัยสำคัญหรือไม่
2. ขนาดของเอฟเฟกต์สามารถใช้เพื่อเปรียบเทียบผลลัพธ์ของการศึกษาต่างๆ ที่ดำเนินการในสภาพแวดล้อมที่แตกต่างกันได้ ซึ่งต่างจากค่า p ด้วยเหตุนี้ จึงมักใช้ขนาดเอฟเฟกต์ในการวิเคราะห์เมตา
3. ค่า P อาจได้รับผลกระทบจากขนาดตัวอย่างขนาดใหญ่ ยิ่งขนาดตัวอย่างใหญ่ขึ้น การทดสอบสมมติฐานก็จะยิ่งมีพลังทางสถิติมากขึ้น ทำให้สามารถตรวจจับผลกระทบแม้เพียงเล็กน้อยได้ ซึ่งอาจส่งผลให้ค่า p ต่ำ แม้ว่าเอฟเฟกต์จะมีขนาดเล็กน้อยซึ่งอาจไม่มีความสำคัญในทางปฏิบัติก็ตาม
ตัวอย่างง่ายๆ สามารถอธิบายสิ่งนี้ได้อย่างชัดเจน: สมมติว่าเราต้องการทราบว่าเทคนิคการศึกษาสองเทคนิคนำไปสู่คะแนนการทดสอบที่แตกต่างกันหรือไม่ เรามีกลุ่มนักเรียน 20 คนที่ใช้เทคนิคการเรียนแบบหนึ่ง ในขณะที่อีกกลุ่มหนึ่งมีนักเรียน 20 คนใช้เทคนิคการเรียนที่แตกต่างกัน จากนั้นเราจะให้นักเรียนแต่ละคนทำแบบทดสอบเดียวกัน
คะแนนเฉลี่ยของกลุ่มที่ 1 คือ 90.65 และคะแนนเฉลี่ยของกลุ่มที่ 2 คือ 90.75 ค่าเบี่ยงเบนมาตรฐานสำหรับตัวอย่างที่ 1 คือ 2.77 และค่าเบี่ยงเบนมาตรฐานสำหรับตัวอย่างที่ 2 คือ 2.78
เมื่อเราทำการทดสอบทีแบบอิสระสองตัวอย่าง ปรากฎว่าสถิติการทดสอบคือ -0.113 และค่า p ที่สอดคล้องกันคือ 0.91 ความแตกต่างระหว่างคะแนนสอบเฉลี่ยไม่มีนัยสำคัญทางสถิติ
อย่างไรก็ตาม ให้พิจารณาว่าขนาดตัวอย่างของทั้งสองตัวอย่างมีค่าเท่ากับ 200 หรือไม่ แต่ค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานยังคงเหมือนเดิมทุกประการ
ในกรณีนี้ การทดสอบทีแบบอิสระสองตัวอย่างจะเผยให้เห็นว่าสถิติการทดสอบคือ -1.97 และค่า p ที่สอดคล้องกันนั้นต่ำกว่า 0.05 เพียงเล็กน้อย ความแตกต่างระหว่างคะแนนสอบเฉลี่ยมีนัยสำคัญทางสถิติ
สาเหตุเบื้องหลังว่าทำไมตัวอย่างขนาดใหญ่จึงสามารถนำไปสู่ข้อสรุปที่มีนัยสำคัญทางสถิติได้เนื่องมาจากสูตรที่ใช้ในการคำนวณสถิติ การทดสอบที :
สถิติทดสอบ t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
โปรดทราบว่าเมื่อ n 1 และ n 2 มีขนาดเล็ก ตัวส่วนจำนวนเต็มของสถิติ t -test จะมีค่าน้อย และเมื่อคุณหารด้วยจำนวนน้อย คุณจะได้จำนวนมาก. ซึ่งหมายความว่าสถิติของการทดสอบ ที จะมีขนาดใหญ่ และค่า p ที่สอดคล้องกันจะมีน้อย ซึ่งนำไปสู่ผลลัพธ์ที่มีนัยสำคัญทางสถิติ
ขนาดเอฟเฟกต์ที่ดีถือว่าเท่าไหร่?
คำถามที่นักเรียนมักถามคือ ขนาดเอฟเฟกต์ที่ดีจะถือว่ามีขนาดเท่าใด
คำตอบสั้นๆ: ขนาดของเอฟเฟกต์ไม่สามารถเป็น “ดี” หรือ “ไม่ดี” ได้ เนื่องจากเป็นเพียงการวัดขนาดของความแตกต่างระหว่างสองกลุ่มหรือจุดแข็งของความสัมพันธ์ระหว่างสองกลุ่ม
อย่างไรก็ตาม เราสามารถใช้กฎง่ายๆ ต่อไปนี้เพื่อระบุปริมาณว่าขนาดของเอฟเฟกต์มีขนาดเล็ก กลาง หรือใหญ่:
D ของโคเฮน:
- d 0.2 หรือน้อยกว่าถือเป็นขนาดเอฟเฟกต์ขนาดเล็ก
- d 0.5 ถือเป็นขนาดเอฟเฟกต์ปานกลาง
- d 0.8 ขึ้นไปถือเป็นขนาดเอฟเฟกต์ขนาดใหญ่
สัมประสิทธิ์สหสัมพันธ์เพียร์สัน
- ค่าสัมบูรณ์ของ r ประมาณ 0.1 ถือเป็นขนาดเอฟเฟกต์ขนาดเล็ก
- ค่าสัมบูรณ์ของ r ประมาณ 0.3 ถือเป็นขนาดเอฟเฟกต์ขนาดกลาง
- ค่าสัมบูรณ์ของ r ที่มากกว่า 0.5 ถือเป็นขนาดเอฟเฟกต์ขนาดใหญ่
อย่างไรก็ตาม คำจำกัดความของความสัมพันธ์ที่ “แข็งแกร่ง” อาจแตกต่างกันไปในแต่ละฟิลด์ อ่าน บทความนี้ เพื่อทำความเข้าใจสิ่งที่ถือเป็นความสัมพันธ์ที่แข็งแกร่งในอุตสาหกรรมต่างๆ