วิธีการคำนวณข้อผิดพลาดมาตรฐานของค่าเฉลี่ยใน excel

ค่าคลาดเคลื่อนมาตรฐานของค่าเฉลี่ย เป็นวิธีการวัดการกระจายของค่าในชุดข้อมูล มีการคำนวณดังนี้:

ข้อผิดพลาดมาตรฐาน = s / √n

ทอง:

• s : ค่าเบี่ยงเบนมาตรฐานตัวอย่าง
• n : ขนาดตัวอย่าง

คุณสามารถคำนวณข้อผิดพลาดมาตรฐานของค่าเฉลี่ยของชุดข้อมูลใดๆ ใน Excel ได้โดยใช้สูตรต่อไปนี้:

= STDEV (ช่วงของค่า) / SQRT ( COUNT (ช่วงของค่า))

ตัวอย่างต่อไปนี้แสดงวิธีการใช้สูตรนี้

ตัวอย่าง: ข้อผิดพลาดมาตรฐานใน Excel

สมมติว่าเรามีชุดข้อมูลต่อไปนี้:

ภาพหน้าจอต่อไปนี้แสดงวิธีคำนวณค่าคลาดเคลื่อนมาตรฐานของค่าเฉลี่ยสำหรับชุดข้อมูลนี้:

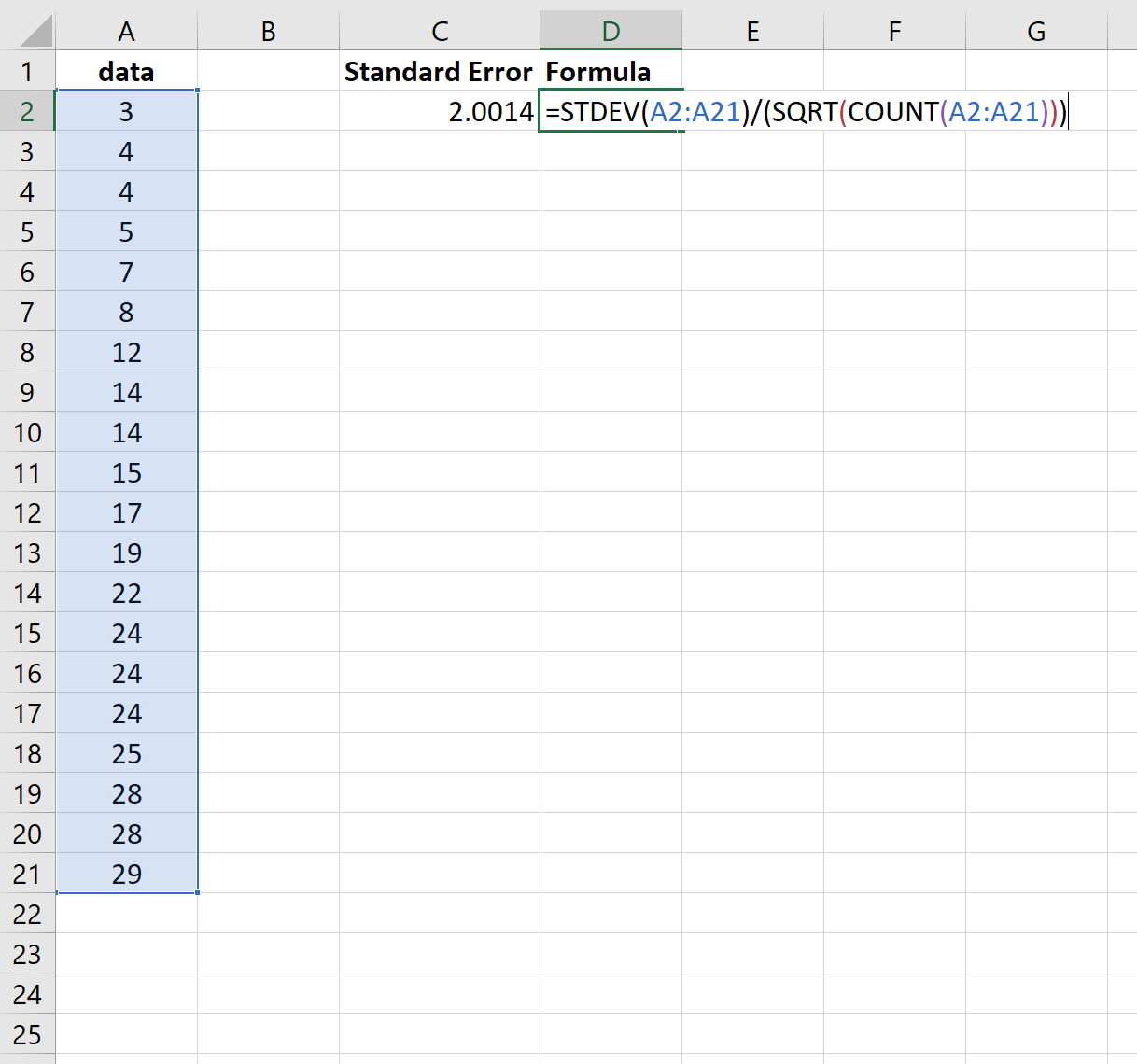
ข้อผิดพลาดมาตรฐานกลายเป็น 2.0014

โปรดทราบว่าฟังก์ชัน =STDEV() จะคำนวณค่าเฉลี่ยตัวอย่าง ซึ่งเทียบเท่ากับฟังก์ชัน =STDEV.S() ใน Excel

ดังนั้นเราจึงสามารถใช้สูตรต่อไปนี้เพื่อให้ได้ผลลัพธ์ที่เหมือนกัน:

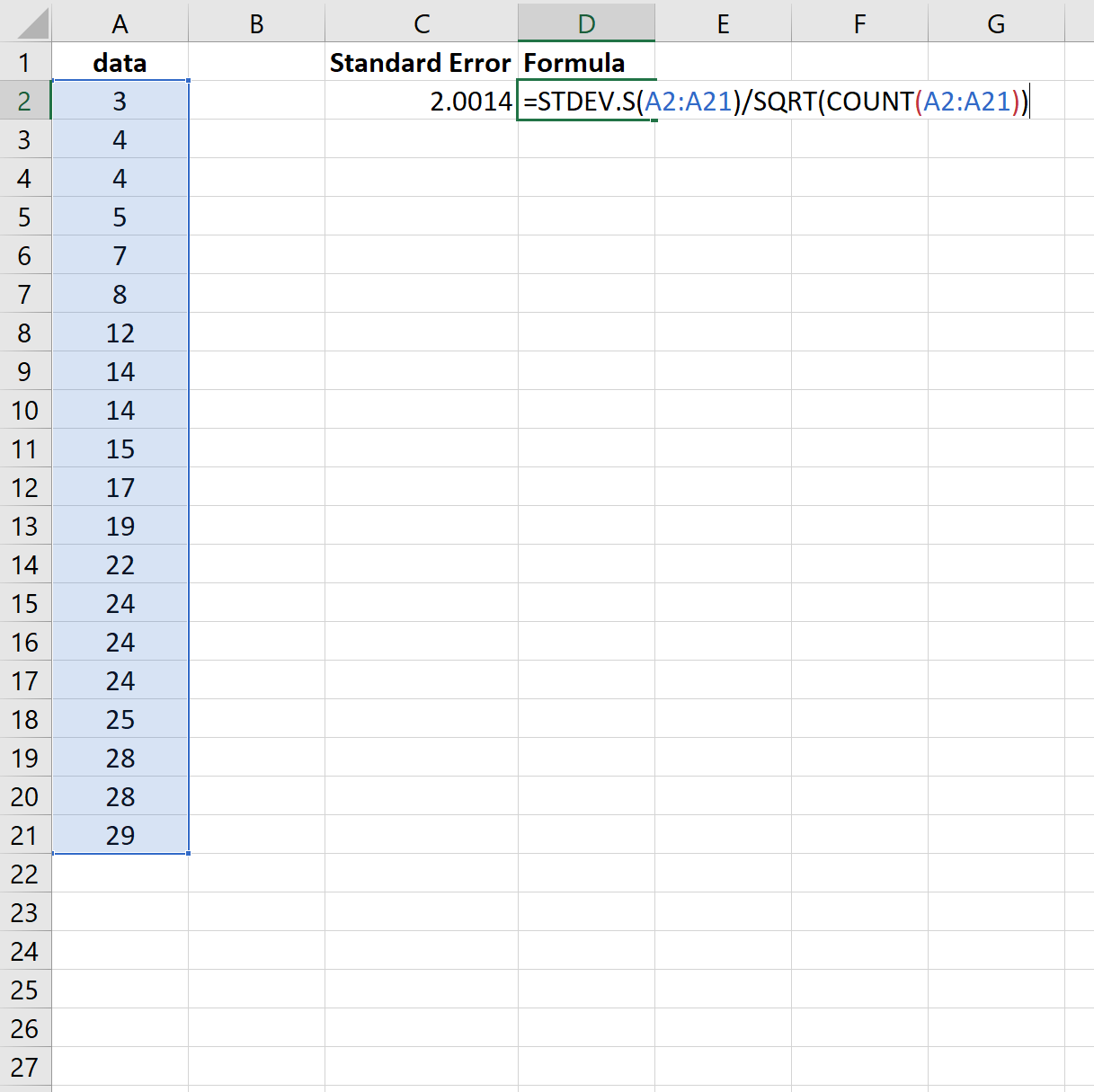
อีกครั้งที่ข้อผิดพลาดมาตรฐานกลายเป็น 2.0014

วิธีตีความความคลาดเคลื่อนมาตรฐานของค่าเฉลี่ย

ค่าคลาดเคลื่อนมาตรฐานของค่าเฉลี่ยเป็นเพียงการวัดการแพร่กระจายของค่ารอบค่าเฉลี่ย มีสองสิ่งที่ต้องคำนึงถึงเมื่อตีความค่าคลาดเคลื่อนมาตรฐานของค่าเฉลี่ย:

1. ยิ่งค่าคลาดเคลื่อนมาตรฐานของค่าเฉลี่ยมากเท่าใด ค่าที่กระจายอยู่รอบๆ ค่าเฉลี่ยในชุดข้อมูลก็จะยิ่งมากขึ้นเท่านั้น

เพื่ออธิบายสิ่งนี้ ให้พิจารณาว่าเราเปลี่ยนค่าสุดท้ายของชุดข้อมูลก่อนหน้าด้วยจำนวนที่มากกว่ามากหรือไม่:

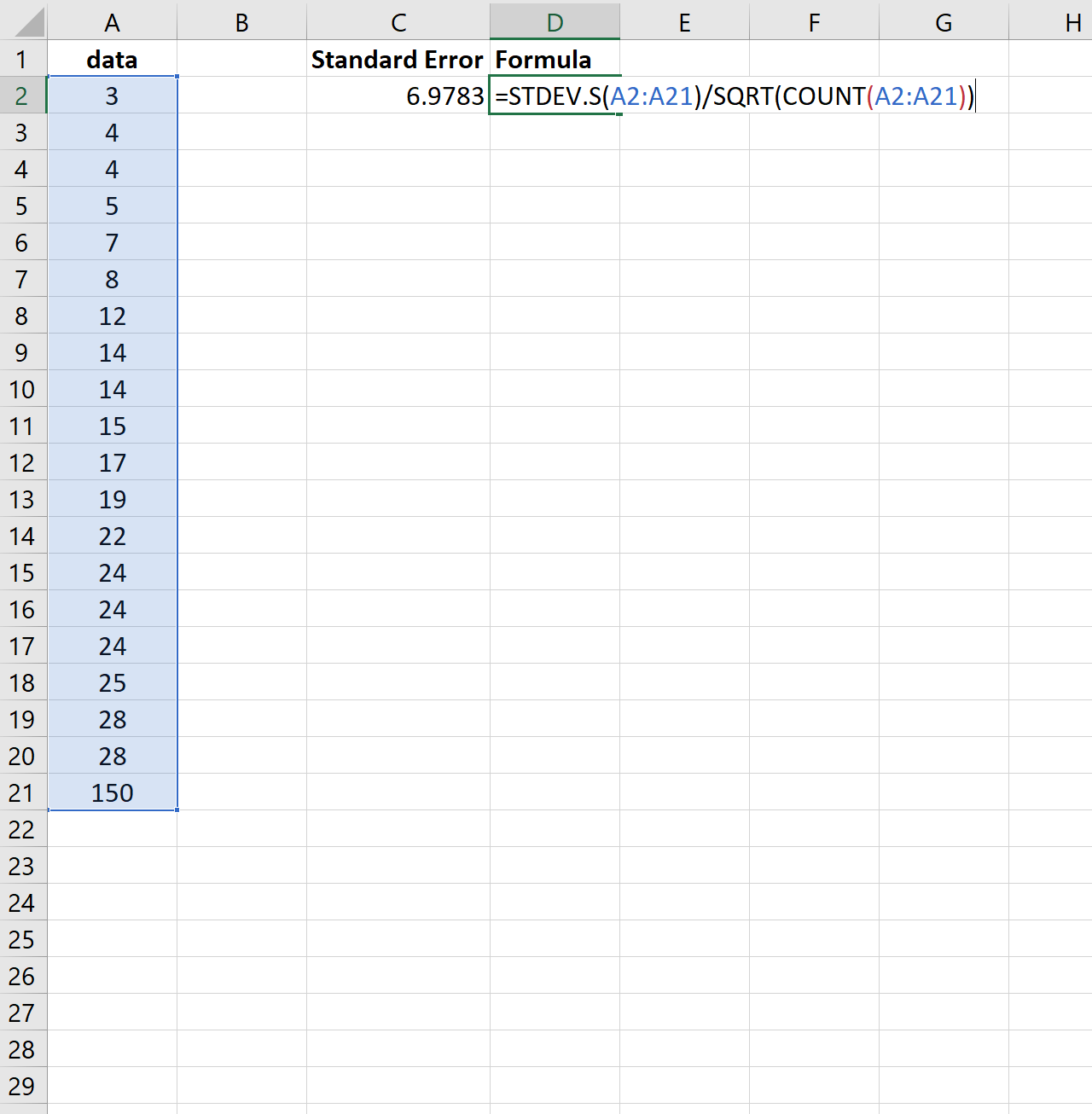
สังเกตว่าข้อผิดพลาดมาตรฐานเพิ่มขึ้นจาก 2.0014 เป็น 6.9783 อย่างไร สิ่งนี้บ่งชี้ว่าค่าในชุดข้อมูลนี้มีการกระจายตามค่าเฉลี่ยมากกว่าเมื่อเทียบกับชุดข้อมูลก่อนหน้า

2. เมื่อขนาดตัวอย่างเพิ่มขึ้น ความคลาดเคลื่อนมาตรฐานของค่าเฉลี่ยมีแนวโน้มลดลง

เพื่ออธิบายสิ่งนี้ ให้พิจารณาความคลาดเคลื่อนมาตรฐานของค่าเฉลี่ยสำหรับข้อมูลสองชุดต่อไปนี้:

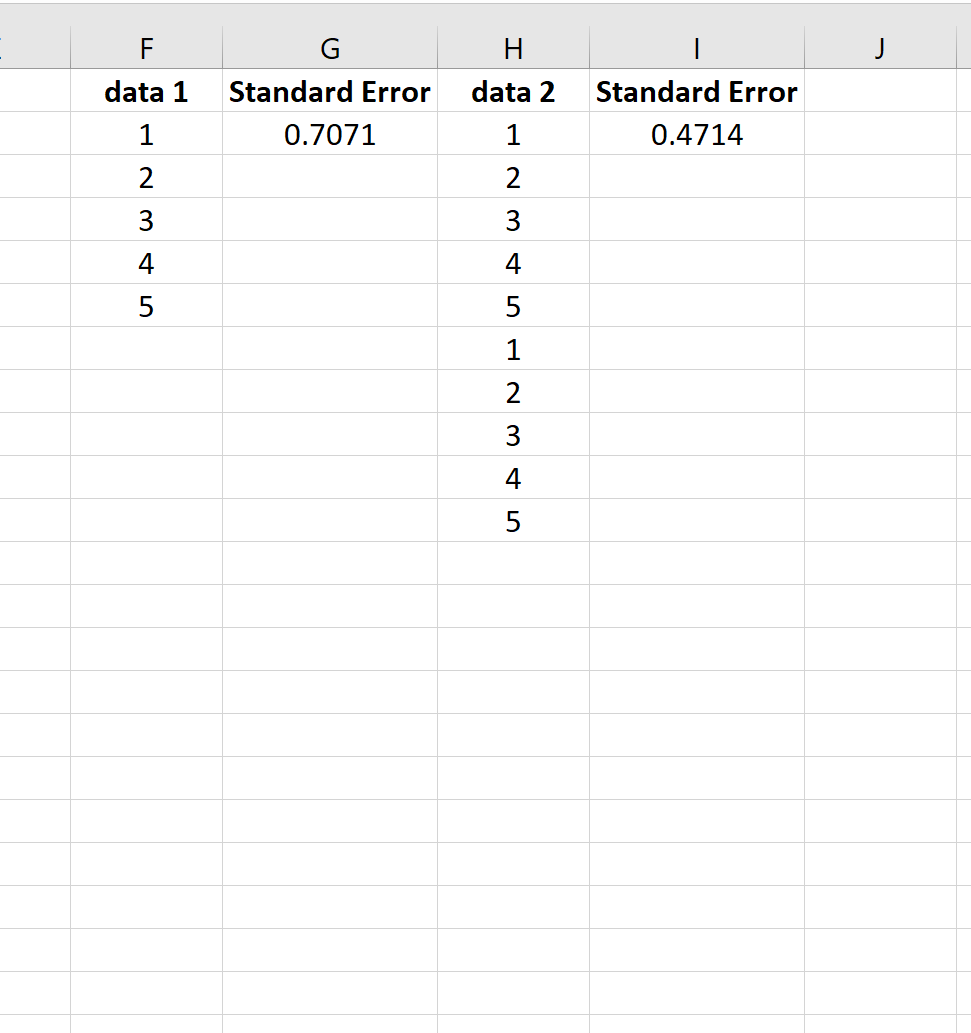
ชุดข้อมูลที่สองเป็นเพียงชุดข้อมูลชุดแรกที่ถูกทำซ้ำสองครั้ง ดังนั้นชุดข้อมูลทั้งสองชุดจึงมีค่าเฉลี่ยเท่ากัน แต่ชุดข้อมูลชุดที่สองมีขนาดตัวอย่างที่ใหญ่กว่า จึงมีข้อผิดพลาดมาตรฐานน้อยกว่า