ควอร์ไทล์

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

ในบทความนี้ เราจะอธิบายว่าควอไทล์คืออะไร คุณจะพบคำจำกัดความของแต่ละควอร์ไทล์ วิธีคำนวณ และตัวอย่างที่เป็นรูปธรรมหลายประการ นอกจากนี้เรายังแสดงวิธีคำนวณควอไทล์สำหรับข้อมูลที่จัดกลุ่มอีกด้วย นอกจากนี้ คุณยังสามารถคำนวณควอไทล์ของชุดข้อมูลใดๆ ได้ด้วยเครื่องคิดเลขออนไลน์

ควอไทล์คืออะไร?

ในสถิติ ควอไทล์คือค่าสามค่าที่แบ่งชุดข้อมูลที่เรียงลำดับออกเป็นสี่ส่วนเท่าๆ กัน ดังนั้นควอร์ไทล์ที่หนึ่ง สอง และสามจึงคิดเป็น 25%, 50% และ 75% ของข้อมูลทางสถิติทั้งหมดตามลำดับ

ควอไทล์แสดงด้วยตัวพิมพ์ใหญ่ Q และดัชนีควอร์ไทล์ ดังนั้นควอไทล์แรกคือ Q ₁ ควอไทล์ที่สองคือ Q ₂ และควอร์ไทล์ที่สามคือ Q ₃

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณควอไทล์ของชุดข้อมูลใดก็ได้

ควรสังเกตว่าควอไทล์เป็นการวัดตำแหน่งที่ไม่อยู่ตรงกลางในลักษณะเดียวกับควินไทล์ เดซิล และเปอร์เซ็นไทล์ คุณสามารถตรวจสอบได้ว่าแต่ละประเภทควอนไทล์เหล่านี้คืออะไรบนหน้าเว็บนี้

ควอไทล์แรก

ควอไทล์แรก หรือที่เรียกว่าควอไทล์ 1 คือค่าที่มากกว่า 25% ของข้อมูลทางสถิติในตัวอย่าง กล่าวอีกนัยหนึ่ง ควอไทล์แรกแสดงถึงมากกว่า 25% ของข้อมูลที่สังเกตได้

ควอไทล์แรกแสดงด้วยสัญลักษณ์ Q ₁ และใช้เพื่อแสดงถึงค่าข้อมูลที่น้อยที่สุดในตัวอย่าง

ควอไทล์ที่สอง

ควอไทล์ที่ 2 หรือที่เรียกว่าควอร์ไทล์ 2 คือค่าที่มากกว่า 50% ของข้อมูลทางสถิติในตัวอย่าง ดังนั้นควอไทล์ที่สองจะแยกข้อมูลออกเป็นสองซีกและตรงกับค่ามัธยฐานและเดไซล์ที่ห้า

สัญลักษณ์ของควอไทล์ที่ 2 คือ _Q2

ควอร์ไทล์ที่สาม

ควอไทล์ที่ 3 หรือที่เรียกว่าควอไทล์ที่ 3 คือค่าที่เกิน 75% ของข้อมูลทางสถิติในตัวอย่าง กล่าวอีกนัยหนึ่ง ควอไทล์ที่สามแสดงถึงมากกว่า 75% ของข้อมูลที่รวบรวม

ควอร์ไทล์ที่สามแสดงด้วยสัญลักษณ์ Q ₃ และแสดงถึงค่าที่ใหญ่ที่สุดในกลุ่มตัวอย่าง

วิธีการคำนวณควอไทล์

ใน การคำนวณตำแหน่งของควอไทล์ ของชุดข้อมูลทางสถิติ คุณต้องคูณจำนวนควอร์ไทล์ด้วยผลรวมของจำนวนข้อมูลทั้งหมดบวกหนึ่ง แล้วหารผลลัพธ์ด้วยสี่

สูตรสำหรับควอร์ไทล์ จึงเป็นดังนี้:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

โปรดทราบ: สูตรนี้บอกเราถึงตำแหน่งของควอไทล์ ไม่ใช่ค่าของควอไทล์ ควอไทล์จะเป็นข้อมูลที่อยู่ในตำแหน่งที่ได้จากสูตร

อย่างไรก็ตาม บางครั้งผลลัพธ์ของสูตรนี้จะทำให้เราได้เลขทศนิยม ดังนั้นเราจึงต้องแยกแยะสองกรณีขึ้นอยู่กับว่าผลลัพธ์เป็นเลขทศนิยมหรือไม่:

หากผลลัพธ์ของสูตรเป็น ตัวเลขที่ไม่มีทศนิยม ควอ ไทล์คือข้อมูลที่อยู่ในตำแหน่งที่ระบุในสูตรด้านบน
หากผลลัพธ์ของสูตรเป็น ตัวเลขที่มีส่วนทศนิยม ค่าควอไทล์จะคำนวณโดยใช้สูตรต่อไปนี้:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

โดยที่ x _i และ x _i+1 คือตัวเลขของตำแหน่งระหว่างตำแหน่งที่มีตัวเลขที่ได้จากสูตรแรกอยู่ และ d คือส่วนทศนิยมของตัวเลขที่ได้จากสูตรแรก

ทีนี้ การคำนวณควอไทล์อาจซับซ้อนมากสำหรับคุณ เพราะมีหลายสิ่งที่ต้องคำนึงถึง แต่ด้วยสองตัวอย่างในส่วนถัดไป คุณจะเห็นว่าจริงๆ แล้วมันค่อนข้างง่ายเพียงใด

หมายเหตุ : ในชุมชนวิทยาศาสตร์ ไม่มีความเห็นพ้องต้องกันเกี่ยวกับวิธีการคำนวณควอไทล์ ดังนั้นคุณจึงสามารถหาหนังสือสถิติที่อธิบายแตกต่างออกไปเล็กน้อยได้

ตัวอย่างการคำนวณควอร์ไทล์

เพื่อให้เข้าใจวิธีคำนวณควอไทล์อย่างถ่องแท้ คุณจะพบแบบฝึกหัดที่แก้ไขแล้วสองแบบฝึกหัดด้านล่างนี้ ควอไทล์แรกเป็นจำนวนเต็มและควอร์ไทล์ที่สองเป็นเลขทศนิยม ดังนั้นคุณจึงดูได้ว่าจะหากรณีใดได้บ้าง

ตัวอย่างที่ 1

คำนวณสามควอไทล์ของชุดข้อมูลต่อไปนี้:

ดังที่เราเห็นข้างต้น สูตรในการกำหนดควอไทล์คือ:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

ในกรณีนี้ n จำนวนการสังเกตทั้งหมดคือ 15 เราจึงต้องแทนที่ n ด้วย 15 และ k ด้วย 1 เพื่อค้นหาควอไทล์แรก:

$\cfrac{1\cdot (15+1)}{4}=4 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_1=39$

ดังนั้น ควอไทล์แรกคือตัวเลขในตำแหน่งที่สี่ของรายการค่าเรียงลำดับ ซึ่งในกรณีนี้คือ 39

ในทำนองเดียวกัน เราคำนวณควอร์ไทล์ที่สองโดยแทนที่สัมประสิทธิ์ k ด้วย 2:

$\cfrac{2\cdot (15+1)}{4}=8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_2=48$

ควอไทล์ 2 จึงเป็นตัวเลขที่แปดในรายการเรียงลำดับ ซึ่งสอดคล้องกับค่า 48

สุดท้าย เราใช้สูตรเป็นครั้งสุดท้ายโดยให้ k =3 เพื่อคำนวณควอไทล์ที่สาม:

$\cfrac{3\cdot (15+1)}{4}=12 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_3=60$

ควอร์ไทล์ที่ 3 สอดคล้องกับข้อมูลในตำแหน่งที่สิบสอง เช่น 60

ตัวอย่างที่ 2

ค้นหาสามควอร์ไทล์ของชุดข้อมูลต่อไปนี้:

ในตัวอย่างที่สองนี้ เรามีข้อสังเกต 24 รายการ ดังนั้นตัวเลขที่ได้จากสูตรควอไทล์จะเป็นทศนิยม

ขั้นแรกเราคำนวณตำแหน่งของควอไทล์แรกโดยการแทนที่ k ด้วย 1 ในสูตรทั่วไป:

$\cfrac{k\cdot (n+1)}{4}$

$\cfrac{1\cdot (24+1)}{4}=6,25$

แต่เราได้เลขฐานสิบ 6.25 ดังนั้นควอไทล์แรกจึงอยู่ระหว่างข้อมูลที่หกและเจ็ด ซึ่งก็คือ 22 และ 25 ตามลำดับ ดังนั้น ในการคำนวณควอไทล์ที่แน่นอน เราจำเป็นต้องใช้สูตรต่อไปนี้:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

ในกรณีนี้ x _i คือ 22, x _i+1 25 และ d เป็นส่วนทศนิยมของตัวเลขที่ได้รับ เช่น 0.25 ยัง:

$Q_1=22+0,25\cdot (25-22)=22,75$

ตอนนี้เราทำขั้นตอนเดียวกันเพื่อค้นหาควอไทล์ที่สอง:

$\cfrac{2\cdot (24+1)}{4}=12,5$

อีกครั้งเราได้รับเลขทศนิยมจากสูตร ในกรณีนี้คือ 12.5 ดังนั้นเราจึงต้องใช้สูตรเดียวกันกับตัวเลขที่สิบสองและสิบสามในตารางข้อมูลซึ่งสอดคล้องกับ 49 และ 50:

$Q_2=49+0,5\cdot (50-49)=49,5$

สุดท้าย เราทำซ้ำขั้นตอนเดียวกันเพื่อให้ได้ควอไทล์ที่สาม:

$\cfrac{3\cdot (24+1)}{4}=18,75$

แต่เลข 18.75 อยู่ระหว่างเลข 18 ถึง 19 ดังนั้นควอร์ไทล์ที่ 3 จะอยู่ระหว่างค่าของตำแหน่งเหล่านี้ (71 และ 73) แม่นยำยิ่งขึ้น นี่จะเป็นค่าที่เราได้รับจากนิพจน์ต่อไปนี้:

$Q_3=71+0,75\cdot (73-71)=72,5$

เครื่องคิดเลขควอไทล์

เสียบข้อมูลทางสถิติที่ตั้งไว้ในเครื่องคิดเลขด้านล่างเพื่อคำนวณควอไทล์ ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

ควอไทล์ในข้อมูลที่จัดกลุ่ม

ใน การคำนวณควอร์ไทล์เมื่อข้อมูลถูกจัดกลุ่มตามช่วงต่างๆ ขั้นแรกเราต้องค้นหาช่วงหรือถังที่ควอร์ไทล์อยู่โดยใช้สูตรต่อไปนี้:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

ควอร์ไทล์จึงอยู่ในช่วงที่ความถี่สะสมสัมบูรณ์มากกว่าจำนวนที่ได้รับจากนิพจน์ก่อนหน้าทันที

และเมื่อเรารู้ช่วงที่เป็นควอไทล์แล้ว เราต้องใช้สูตรต่อไปนี้เพื่อค้นหาค่าที่แน่นอนของควอไทล์:

$Q_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{4}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3$

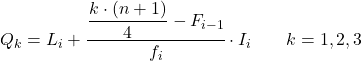
ทอง:

L _i คือขีดจำกัดล่างของช่วงเวลาที่ควอร์ไทล์อยู่
n คือจำนวนการสังเกตทั้งหมด
F _i-1 คือความถี่สัมบูรณ์สะสมของช่วงก่อนหน้า
f _i คือความถี่สัมบูรณ์ของช่วงเวลาที่ควอร์ไทล์อยู่
ฉัน _ฉัน คือความกว้างของช่วงควอไทล์

ตามตัวอย่าง ต่อไปนี้เป็นแบบฝึกหัดในการคำนวณควอร์ไทล์ในชุดข้อมูลที่จัดกลุ่ม:

ในการคำนวณควอไทล์แรก คุณต้องกำหนดช่วงเวลาที่ควอร์ไทล์แรกตกก่อน เมื่อต้องการทำเช่นนี้ เราใช้สูตรต่อไปนี้:

$\cfrac{k\cdot (n+1)}{4}$

$\cfrac{1\cdot (30+1)}{4} =7,75 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [50,60)$

ดังนั้นควอไทล์แรกจะอยู่ในช่วงที่มีความถี่สัมบูรณ์สะสมมากกว่า 7.75 ทันที ในกรณีนี้คือช่วง [50.60) ซึ่งมีความถี่สัมบูรณ์สะสมเท่ากับ 15 และเมื่อเราทราบช่วงควอร์ไทล์แล้ว เราก็ใช้สูตรกระบวนการที่สอง : :

$Q_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{4}-F_{i-1}}{f_i}\cdot I_i$

$Q_1=50+\cfrac{\displaystyle\frac{1\cdot (30+1)}{4}-7}{8}\cdot 10=50,94$

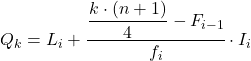
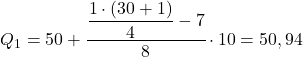
เราใช้ขั้นตอนเดิมอีกครั้งเพื่อให้ได้ควอไทล์ที่สอง ก่อนอื่นเราจะกำหนดช่วงเวลาที่ควอร์ไทล์อยู่:

$\cfrac{2\cdot (30+1)}{4} =15,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

ช่วงความถี่สัมบูรณ์สะสมมากกว่า 15.5 ทันทีคือ [60.70) โดยมีความถี่สัมบูรณ์สะสม 26 ควอไทล์ที่สองจึงเป็น:

$Q_2=60+\cfrac{\displaystyle\frac{2\cdot (30+1)}{4}-15}{11}\cdot 10=60,45$

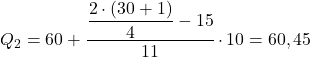
และสุดท้าย เราทำขั้นตอนนี้ซ้ำเพื่อค้นหาควอไทล์ที่สาม ขั้นแรกเราคำนวณช่วงเวลาที่มีควอไทล์:

$\cfrac{3\cdot (30+1)}{4} =22,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

ความถี่สัมบูรณ์สะสมที่สูงกว่า 23.25 ทันทีคือ 26 ดังนั้นช่วงควอไทล์ที่สามคือ [60.70) ดังนั้นเราจึงใช้สูตรในการคำนวณควอร์ไทล์ตามช่วงเวลานี้:

$Q_3=60+\cfrac{\displaystyle\frac{3\cdot (30+1)}{4}-15}{11}\cdot 10=67,5$

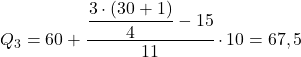
ควอไทล์ใช้ทำอะไร?

ควอร์ไทล์เป็นหน่วยวัดตำแหน่ง ดังนั้นจึงใช้รู้ว่าข้อมูลอยู่ในตำแหน่งใด กล่าวอีกนัยหนึ่ง ค่าของควอร์ไทล์ทั้งสามช่วยให้เราทราบว่ารายการข้อมูลสุ่มในกลุ่มตัวอย่างมีขนาดใหญ่มาก เล็กมาก หรือเป็นค่าเฉลี่ยหรือไม่

หากเราสุ่มเอาข้อมูลชิ้นหนึ่งจากตัวอย่าง เราสามารถบอกได้ว่าค่าของมันสูงหรือต่ำโดยเปรียบเทียบกับควอไทล์ ถ้าค่าข้อมูลสุ่มน้อยกว่าควอไทล์ที่ 1 ก็จะเป็นค่าน้อย แต่ถ้าค่ามากกว่าควอไทล์ที่ 3 ก็จะมีค่ามาก ในทำนองเดียวกัน หากค่าของข้อมูลดังกล่าวอยู่ระหว่างควอร์ไทล์ที่ 1 และ 3 ค่าดังกล่าวจะเป็นค่ากลาง

ในทางกลับกัน ควอร์ไทล์ยังใช้ในการคำนวณหน่วยวัดทางสถิติอื่นๆ เช่น ช่วงระหว่างควอร์ไทล์ (หรือช่วงระหว่างควอไทล์) และเพื่อสร้างไดอะแกรม เช่น พล็อตกล่องและมัสสุ (หรือบ็อกซ์พล็อต)

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

ควอไทล์คืออะไร?

ควอไทล์แรก

ควอไทล์ที่สอง

ควอร์ไทล์ที่สาม

วิธีการคำนวณควอไทล์

ตัวอย่างการคำนวณควอร์ไทล์

ตัวอย่างที่ 1

ตัวอย่างที่ 2

เครื่องคิดเลขควอไทล์

ควอไทล์ในข้อมูลที่จัดกลุ่ม

ควอไทล์ใช้ทำอะไร?

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น