ความถี่ร่วม: คำจำกัดความและตัวอย่าง

ตารางความถี่สองทาง คือตารางที่แสดงความถี่ของตัวแปรประเภทสองตัว

ตัวอย่างเช่น ตารางสองทางต่อไปนี้แสดงผลการสำรวจที่ถามผู้คน 100 คนว่าพวกเขาชอบกีฬาประเภทใด: เบสบอล บาสเก็ตบอล หรือฟุตบอล

แถวแสดงเพศของผู้ตอบแบบสอบถาม และคอลัมน์ระบุกีฬาที่พวกเขาเลือก:

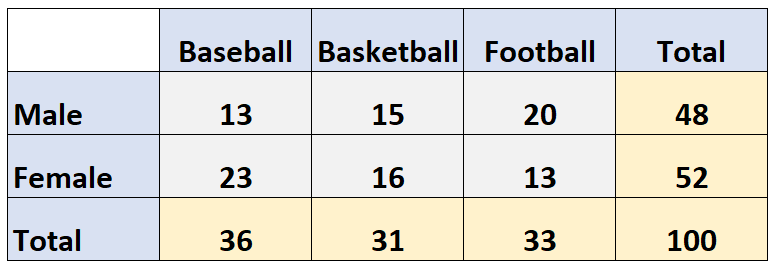
ความถี่ขอบ คือความถี่ที่ระบุในระยะขอบของตาราง:

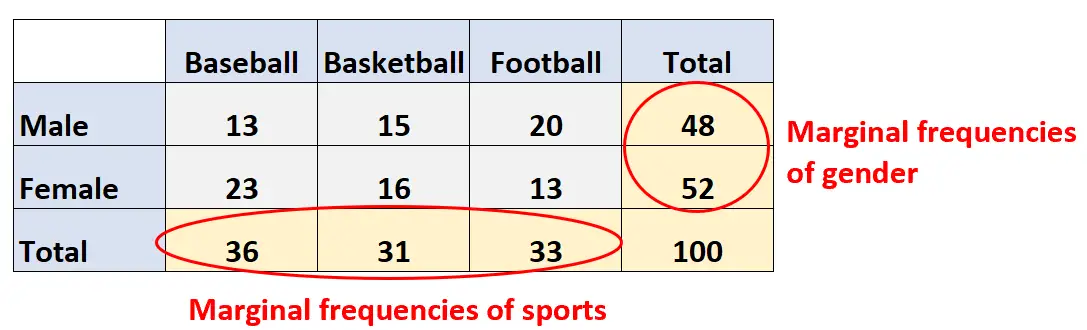
ค่าเหล่านี้บอกเราถึงค่ารวมของแต่ละตัวแปร ตัวอย่างเช่น:

• ผู้ตอบแบบสอบถามทั้งหมด 36 คนเลือกเบสบอลเป็นกีฬาโปรดของพวกเขา
• ผู้ตอบแบบสอบถามทั้งหมด 31 คนเลือกบาสเก็ตบอลเป็นกีฬาโปรดของพวกเขา
• ผู้ตอบแบบสอบถามทั้งหมด 33 คนเลือกฟุตบอลเป็นกีฬาโปรดของพวกเขา

เรายังสามารถดู:

• จำนวนผู้ตอบแบบสอบถามเป็นชายทั้งหมด 48 ราย
• ผู้ตอบแบบสอบถามทั้งหมด 52 คนเป็นผู้หญิง

ความถี่ร่วม คือความถี่ที่แสดงในเซลล์ตาราง:

ค่าเหล่านี้เรียกว่าความถี่ “ร่วม” เนื่องจากบอกเราถึงความถี่ของสองค่าที่เกิดขึ้นร่วมกัน

ตัวอย่างเช่น เราเห็น:

• มีผู้ตอบแบบสอบถามทั้งหมด 13 คนที่เป็นผู้ชาย และ ชอบเล่นเบสบอล
• มีผู้ตอบแบบสอบถามเป็นผู้ชาย และ ชอบเล่นบาสเก็ตบอลทั้งหมด 15 คน
• ผู้ตอบแบบสอบถามทั้งหมด 20 คนเป็นผู้ชาย และ ชอบฟุตบอล
• มีผู้ตอบแบบสอบถามทั้งหมด 23 คนที่เป็นผู้หญิง และ ชอบเล่นเบสบอล
• มีผู้ตอบแบบสอบถามเป็นผู้หญิง และ ชอบเล่นบาสเก็ตบอลทั้งหมด 16 คน
• ผู้ตอบแบบสอบถามทั้งหมด 13 คนเป็นผู้หญิง และ ชอบฟุตบอล

โปรดทราบว่าผลรวมของความถี่ร่วมทั้งหมดสอดคล้องกับจำนวนผู้ตอบแบบสอบถามทั้งหมด:

ผู้ตอบแบบสำรวจทั้งหมด = 13 + 15 + 20 + 23 + 16 + 13 = 100

ความถี่สัมพัทธ์ร่วมคืออะไร?

ความถี่สัมพัทธ์ร่วม บอกเราถึงความถี่ของตัวแปรหนึ่ง ที่สัมพันธ์ กับตัวแปรอื่น

ตัวอย่างเช่น ลองพิจารณาตาราง double-entry ของเราจากก่อนหน้านี้:

คำถามที่ 1: ความถี่สัมพัทธ์ร่วมที่ผู้ตอบแบบสำรวจชอบเบสบอลคือเท่าใด เนื่องจากเป็นผู้หญิง

เพื่อตอบคำถามนี้ เราจะพิจารณาเฉพาะบรรทัดที่มีคำตอบของผู้หญิงเท่านั้น จากนั้นเราจะนำจำนวนผู้หญิงที่ชอบเล่นเบสบอลมาหารด้วยจำนวนผู้หญิงทั้งหมด

นี่กลายเป็น 23/52 = 0.4423 = 44.23%

กล่าวอีกนัยหนึ่ง 44.23% ของผู้ตอบแบบสอบถามหญิงทั้งหมดชอบเบสบอลเป็นกีฬาโปรดของพวกเขา

คำถามที่ 2: ความถี่สัมพัทธ์ร่วมที่ผู้ตอบแบบสำรวจเป็นผู้ชายคือเท่าใด เนื่องจากเขาชอบฟุตบอลเป็นกีฬาโปรดของเขา

เพื่อตอบคำถามนี้ เราจะพิจารณาเฉพาะส่วนที่มีฟุตบอลเป็นกีฬาโปรดของเราเท่านั้น จากนั้นเราจะนำจำนวนผู้ชายที่ชอบฟุตบอลมาหารด้วยจำนวนผู้ตอบแบบสอบถามทั้งหมดที่ชอบฟุตบอล

นี่กลายเป็น 20/33 = 0.606 = 60.6%

กล่าวอีกนัยหนึ่ง 60.6% ของผู้ตอบแบบสำรวจทั้งหมดที่ชื่นชอบฟุตบอลคือผู้ชาย

แหล่งข้อมูลเพิ่มเติม

การกระจายส่วนเพิ่มคืออะไร?
การแจกแจงแบบมีเงื่อนไขคืออะไร
การแจกแจงความน่าจะเป็นร่วมคืออะไร?