ความถี่สัมบูรณ์สะสม

บทความนี้จะอธิบายว่าความถี่สัมบูรณ์สะสมคืออะไร และใช้เพื่ออะไร ดังนั้น คุณจะพบคำจำกัดความของความถี่สัมบูรณ์สะสม วิธีรับความถี่สัมบูรณ์สะสมจากชุดข้อมูล และยังมีแบบฝึกหัดสองบทที่แก้ไขทีละขั้นตอนอีกด้วย

ความถี่สัมบูรณ์สะสมคืออะไร?

ในสถิติ ความถี่สัมบูรณ์สะสม คือผลรวมสะสมของความถี่สัมบูรณ์ นั่นคือความถี่สัมบูรณ์สะสมของค่าจะเท่ากับความถี่สัมบูรณ์ของค่านั้นบวกกับความถี่สัมบูรณ์ของค่าทั้งหมดที่น้อยกว่านั้น

โดยปกติ ในทางสถิติ ตัวอักษร F ตัวพิมพ์ใหญ่ที่มีตัวห้อย i จะใช้แทนความถี่สัมบูรณ์สะสมของค่า i ดังนั้น สัญลักษณ์ของความถี่สัมบูรณ์สะสมคือ F _i

ตามหลักเหตุผล เพื่อทำความเข้าใจว่าความถี่สัมบูรณ์สะสมหมายถึงอะไร คุณต้องเข้าใจแนวคิดเรื่องความถี่สัมบูรณ์ให้ชัดเจน ดังนั้นจึงแนะนำให้ตรวจสอบบทความต่อไปนี้ก่อนที่จะอธิบายต่อ

วิธีการคำนวณความถี่สัมบูรณ์สะสม

ขั้นตอนในการคำนวณความถี่สัมบูรณ์สะสมมีดังนี้:

1. สร้างตารางที่มีค่าต่างๆ ทั้งหมดที่ปรากฏในชุดข้อมูล นั่นคือ วางค่าที่แตกต่างกันแต่ละค่าไว้ในแถวของตาราง
2. กำหนดความถี่สัมบูรณ์ของแต่ละค่า
3. ค้นหาความถี่สัมบูรณ์สะสมของแต่ละค่า ซึ่งคำนวณโดยการบวกความถี่สัมบูรณ์ของค่านั้นบวกกับความถี่สัมบูรณ์ของค่าที่น้อยกว่าทั้งหมด

โปรดทราบว่าหากตัวแปรมีความต่อเนื่องหรือมีค่าที่แตกต่างกันมากมาย คุณต้องจัดกลุ่มข้อมูลเป็นช่วงๆ ก่อน จากนั้นจึงใช้ขั้นตอนที่อธิบายไว้ข้างต้นเพื่อค้นหาความถี่สัมบูรณ์สะสม

ตัวอย่างความถี่สัมบูรณ์สะสม

เพื่อให้คุณสามารถดูวิธีคำนวณความถี่สัมบูรณ์สะสมได้ ด้านล่างนี้คือตัวอย่างการใช้งานจริงสองตัวอย่างทีละขั้นตอน ในตัวอย่างแรก มีการคำนวณความถี่สัมบูรณ์สะสมของตัวแปรที่ไม่ต่อเนื่องและในขั้นตอนที่สองของตัวแปรต่อเนื่อง

ตัวอย่างที่ 1: ตัวแปรไม่ต่อเนื่อง

• คะแนนที่ได้รับทางสถิติในชั้นเรียนจำนวน 30 คน มีดังนี้ ความถี่สัมบูรณ์สะสมของแต่ละโน้ตคือเท่าใด

เนื่องจากตัวเลขทั้งหมดสามารถเป็นจำนวนเต็มได้เท่านั้น จึงเป็นตัวแปรที่ไม่ต่อเนื่อง จึงไม่จำเป็นที่จะต้องจัดกลุ่มข้อมูลเป็นระยะๆ

ดังนั้น ในการหาความถี่สัมบูรณ์สะสม อันดับแรกเราต้องค้นหาความถี่สัมบูรณ์ของแต่ละค่า ซึ่งเป็นจำนวนครั้งที่แต่ละค่าปรากฏในตัวอย่างทางสถิติ

ตอนนี้เรารู้ความถี่สัมบูรณ์แล้ว เราก็สามารถคำนวณความถี่สัมบูรณ์สะสมได้ ในการทำเช่นนี้ เรามีสองทางเลือก: เราจะเพิ่มความถี่สัมบูรณ์ของค่าบวกกับความถี่สัมบูรณ์ทั้งหมดของค่าที่เล็กที่สุด หรือในทางกลับกัน เราจะเพิ่มความถี่สัมบูรณ์ของค่าบวกด้วยความถี่สัมบูรณ์สะสมของค่าก่อนหน้า . ค่า.

สรุปตารางความถี่สะสมสัมบูรณ์ของการออกกำลังกายมีดังนี้:

โปรดทราบว่าความถี่สัมบูรณ์สะสมของค่าสุดท้ายจะสอดคล้องกับจำนวนข้อมูลทั้งหมดเสมอ มิฉะนั้นก็หมายความว่าคุณทำผิดพลาดในการคำนวณ

ตัวอย่างที่ 2: ตัวแปรต่อเนื่อง

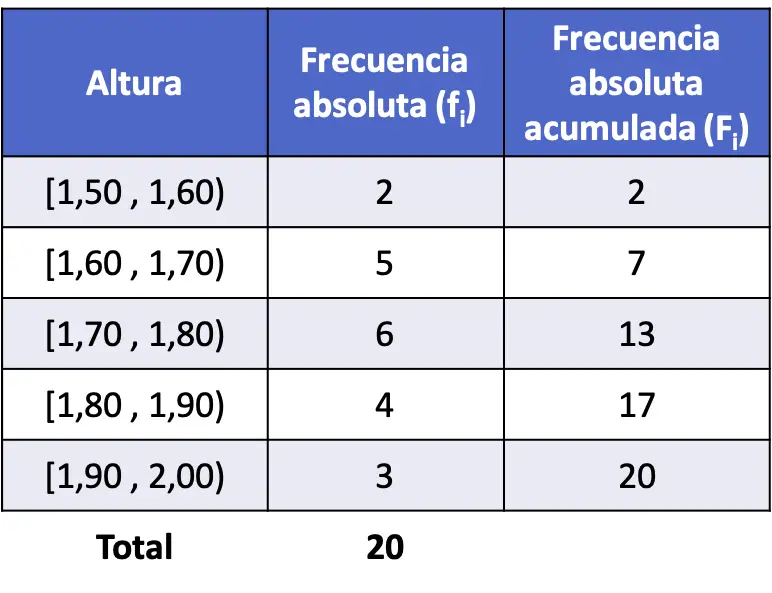
• วัดส่วนสูงจำนวน 20 คน และได้ผลลัพธ์ที่แสดงด้านล่าง แยกข้อมูลออกเป็นช่วงๆ และคำนวณความถี่สัมบูรณ์สะสมสำหรับแต่ละช่วงเวลา

การแจกแจงในตัวอย่างนี้เป็นแบบต่อเนื่อง เนื่องจากอาจเป็นเลขทศนิยมได้ ดังนั้นจึงควรจัดกลุ่มข้อมูลตามช่วงเวลาที่ต่างกัน

ดังนั้นเราจึงแยกข้อมูลออกเป็นระยะๆ และนับจำนวนครั้งที่ตัวเลขปรากฏในแต่ละช่วงเวลาเพื่อให้ได้ความถี่สัมบูรณ์:

จากนั้นเพื่อกำหนดความถี่สัมบูรณ์สะสมเพียงเพิ่มความถี่สัมบูรณ์ของค่าก่อนหน้าทั้งหมดบวกกับความถี่สัมบูรณ์ของค่าที่ต้องการ:

ความถี่สัมบูรณ์สะสมและความถี่สัมพัทธ์สะสม

ความแตกต่างระหว่างความถี่สัมบูรณ์สะสมและความถี่สัมพัทธ์สะสม สอดคล้องกับประเภทความถี่สะสม ความถี่สัมพัทธ์สะสมจะเท่ากับผลรวมของความถี่สัมบูรณ์ของค่าที่เท่ากันหรือต่ำกว่า ในขณะที่ความถี่สัมพัทธ์สะสมจะเทียบเท่ากับความถี่สัมพัทธ์ของค่าที่เท่ากันหรือต่ำกว่า

ดังนั้นความถี่สัมพัทธ์สะสมจะคำนวณจากความถี่สัมพัทธ์ ในขณะที่ความถี่สัมพัทธ์สะสมจะคำนวณจากความถี่สัมพัทธ์

คุณสามารถดูตัวอย่างการคำนวณความถี่สัมพัทธ์สะสมได้ที่นี่: