ความถี่สัมพัทธ์
ในบทความนี้ คุณจะได้เรียนรู้ว่าความถี่สัมพัทธ์ในสถิติคืออะไร วิธีหาความถี่สัมพัทธ์ และแบบฝึกหัดสองขั้นตอนเกี่ยวกับความถี่สัมพัทธ์ที่ได้รับการแก้ไขทีละขั้นตอน
ความถี่สัมพัทธ์คืออะไร?
ในสถิติ ความถี่สัมพัทธ์ คือหน่วยวัดที่ระบุจำนวนครั้งที่ค่าปรากฏในตัวอย่างข้อมูลเป็นสัดส่วนหรือเปอร์เซ็นต์ ความถี่สัมพัทธ์จะเท่ากับความถี่สัมบูรณ์หารด้วยจำนวนข้อมูลทั้งหมด
ตัวอย่างเช่น ถ้าความถี่สัมบูรณ์ของค่าคือ 15 และมีจุดข้อมูลทั้งหมด 100 จุด ความถี่สัมพัทธ์ของค่านั้นจะเท่ากับ 0.15 (15/100=0.15)
โดยทั่วไปสัญลักษณ์ h i ใช้แทนความถี่สัมพัทธ์ แม้ว่าจะยังไม่มีความเห็นพ้องต้องกันในชุมชนทางสถิติ ดังนั้นคุณจึงสามารถเห็นความถี่สัมพัทธ์ที่แสดงโดยสัญลักษณ์อื่นได้
วิธีการคำนวณความถี่สัมพัทธ์
ความถี่สัมพัทธ์เท่ากับความถี่สัมบูรณ์หารด้วยจำนวนข้อมูลทั้งหมด ดังนั้น ในการคำนวณความถี่สัมพัทธ์ คุณต้องหาความถี่สัมบูรณ์ก่อนแล้วจึงหารด้วยจำนวนการสังเกตทั้งหมด
ดังนั้น สูตรหาความถี่สัมพัทธ์ จึงเป็นดังนี้
![]()
ทอง:
-
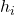
คือความถี่สัมพัทธ์
-

คือความถี่สัมบูรณ์
-

คือจำนวนข้อมูลทั้งหมด
ในทางกลับกัน หากต้องการคำนวณ ความถี่สัมพัทธ์เป็นเปอร์เซ็นต์ กล่าวคือความถี่สัมพัทธ์ที่แสดงเป็นเปอร์เซ็นต์ เพียงคูณสูตรก่อนหน้าด้วย 100:
![]()
ตัวอย่างความถี่สัมพัทธ์
เมื่อคุณได้เห็นคำจำกัดความของความถี่สัมพัทธ์แล้ว ด้านล่างนี้คือตัวอย่างสองตัวอย่างที่เกิดขึ้นจริงเพื่อให้คุณเห็นว่าความถี่ประเภทนี้มีการคำนวณอย่างไร ในตัวอย่างแรก ความถี่สัมพัทธ์ของตัวแปรแยกจะถูกกำหนด และในตัวอย่างที่สอง จะเป็นตัวแปรต่อเนื่อง
ตัวอย่างที่ 1: ตัวแปรไม่ต่อเนื่อง
- คะแนนที่ได้รับในวิชาสถิติในชั้นเรียนจำนวน 30 คน มีดังนี้ ความถี่สัมพัทธ์ของแต่ละโน้ตคือเท่าใด
![]()
![]()
![]()
ตัวแปรในแบบฝึกหัดนี้แยกจากกันเนื่องจากข้อมูลต้องเป็นจำนวนเต็มเท่านั้น ดังนั้นจึงไม่จำเป็นต้องจัดกลุ่มข้อมูลเป็นช่วงๆ
เพื่อที่จะหาความถี่สัมพัทธ์ เราต้องกำหนดความถี่สัมบูรณ์ก่อน ดังนั้นเราจึงสร้างตารางความถี่และคำนวณความถี่สัมบูรณ์สำหรับค่าที่แตกต่างกันแต่ละค่า:

ตอนนี้เราได้คำนวณความถี่สัมบูรณ์แล้ว เราก็สามารถคำนวณความถี่สัมพัทธ์ได้ เมื่อต้องการทำเช่นนี้ เพียงหารแต่ละความถี่สัมบูรณ์ด้วยจำนวนข้อมูลทั้งหมด (30):
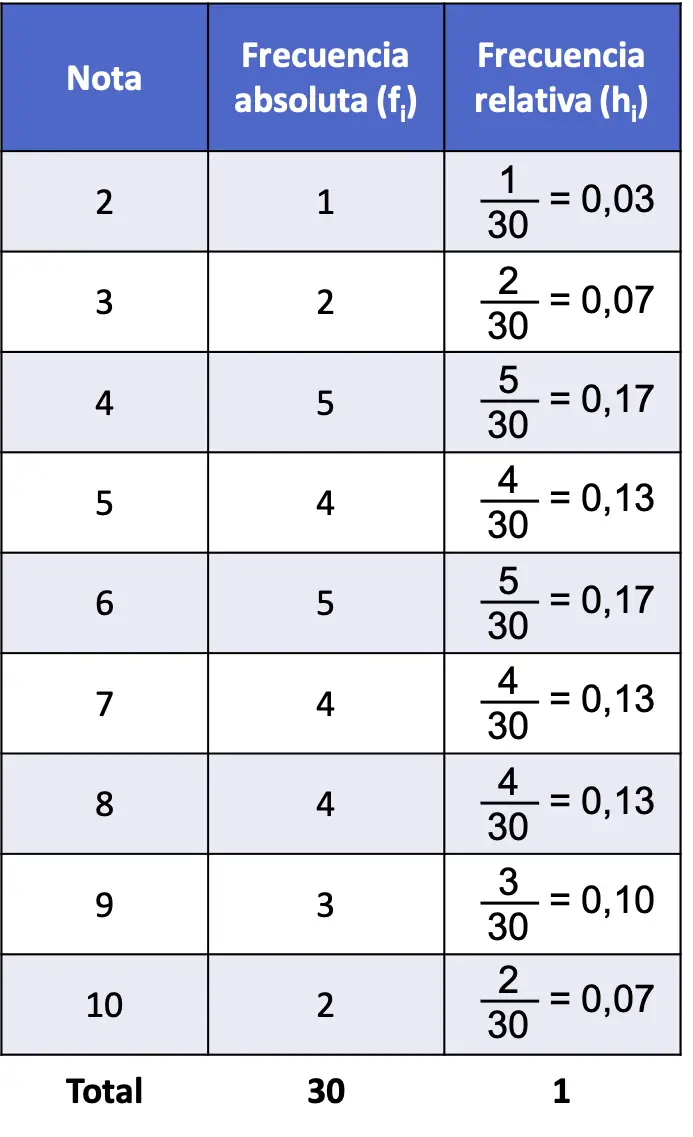
ดังนั้น ตารางความถี่ของปัญหาความถี่สัมบูรณ์และความถี่สัมพัทธ์จะเป็นดังนี้

โปรดทราบว่าผลรวมของความถี่สัมพัทธ์ทั้งหมดจะให้ 1 เสมอ ไม่เช่นนั้นก็หมายความว่าการคำนวณบางอย่างผิดพลาด
ตัวอย่างที่ 2: ตัวแปรต่อเนื่อง
- วัดส่วนสูงจำนวน 20 คน และได้ผลลัพธ์ตามที่ระบุไว้ด้านล่าง แยกข้อมูลออกเป็นช่วงๆ และค้นหาความถี่สัมพัทธ์ของแต่ละช่วง
![]()
![]()
ข้อมูลในตัวอย่างทางสถิตินี้เป็นของตัวแปรต่อเนื่อง เนื่องจากเป็นตัวเลขทศนิยม ดังนั้น ตัวแปรจึงสามารถรับค่าใดๆ ก็ได้ ดังนั้น ก่อนที่จะคำนวณความถี่ เราจะจัดกลุ่มข้อมูลออกเป็นช่วงๆ โดยมีแอมพลิจูด 10/10
ต่อไป เราจะสร้างตารางความถี่ที่มีความถี่สัมบูรณ์ของแต่ละช่วงเวลา:

และเมื่อเราพบความถี่สัมบูรณ์แล้ว เราก็จะได้ความถี่สัมพัทธ์ของแต่ละช่วงเวลาได้โดยการหารความถี่สัมบูรณ์ด้วยจำนวนข้อมูลทั้งหมด (20)

ความถี่สัมพัทธ์สะสม
ตามชื่อที่แสดง ความถี่สัมพัทธ์สะสมเป็นความถี่อีกประเภทหนึ่งที่ใช้ในสถิติและคำนวณจากความถี่สัมพัทธ์
แม่นยำยิ่งขึ้น ความถี่สัมพัทธ์สะสม ของค่าจะเท่ากับผลรวมของความถี่สัมพัทธ์ของค่านั้นบวกกับความถี่สัมพัทธ์ของค่าที่น้อยกว่าทั้งหมด
เพื่อให้คุณสามารถดูวิธีการรับความถี่สัมพัทธ์สะสม ความถี่สัมพัทธ์สะสมของชุดข้อมูลในตัวอย่างแรกได้รับการคำนวณด้านล่าง:
