ความถี่สัมพัทธ์สะสม

บทความนี้จะอธิบายว่าความถี่สัมพัทธ์สะสมในสถิติคืออะไร ดังนั้นคุณจะพบคำจำกัดความของความถี่สัมพัทธ์สะสม วิธีรับความถี่สัมพัทธ์สะสม และแบบฝึกหัดสองข้อที่แก้ไขทีละขั้นตอน

ความถี่สัมพัทธ์สะสมคืออะไร?

ในสถิติ ความถี่สัมพัทธ์สะสม คือผลรวมสะสมของความถี่สัมพัทธ์ นั่นคือความถี่สัมพัทธ์สะสมของค่าจะเท่ากับความถี่สัมพัทธ์ของค่านั้นบวกกับความถี่สัมพัทธ์ของค่าทั้งหมดที่น้อยกว่านั้น

สัญลักษณ์สำหรับความถี่สัมพัทธ์สะสมคือ H _i อย่างไรก็ตาม ในสถิติยังไม่มีความเห็นพ้องต้องกันอย่างสมบูรณ์เกี่ยวกับสัญลักษณ์สำหรับความถี่ประเภทนี้ ซึ่งเป็นสาเหตุที่คุณอาจพบว่ามีการแสดงสัญลักษณ์ดังกล่าวโดยใช้สัญลักษณ์อื่น

แน่นอนว่าเพื่อที่จะเข้าใจความหมายของความถี่สัมพัทธ์สะสม คุณต้องเข้าใจแนวคิดเรื่องความถี่สัมพัทธ์ให้ชัดเจนก่อน ซึ่งเป็นสาเหตุที่ฉันแนะนำให้คุณไปที่ลิงก์ต่อไปนี้ก่อนจะอธิบายต่อ:

วิธีการคำนวณความถี่สัมพัทธ์สะสม

ในการ คำนวณความถี่สัมพัทธ์สะสม ต้องปฏิบัติตามขั้นตอนต่อไปนี้:

1. สร้างตารางความถี่ที่มีค่าต่าง ๆ ทั้งหมดจากตัวอย่างทางสถิติ
2. คำนวณความถี่สัมบูรณ์ของแต่ละค่า
3. จากความถี่สัมบูรณ์ ให้กำหนดความถี่สัมพัทธ์ของแต่ละค่า
4. ค้นหาความถี่สัมพัทธ์สะสมของแต่ละค่า ซึ่งคำนวณโดยการบวกความถี่สัมพัทธ์ของค่านั้นบวกกับความถี่สัมพัทธ์ของค่าที่น้อยกว่าทั้งหมด

โปรดทราบว่าหากคุณต้องการคำนวณ เปอร์เซ็นต์ความถี่สัมพัทธ์สะสม ซึ่งก็คือความถี่สัมพัทธ์สะสมที่แสดงเป็นเปอร์เซ็นต์ คุณเพียงแค่ต้องทำตามขั้นตอนเดียวกันและคูณผลลัพธ์ด้วย 100

ตัวอย่างความถี่สัมพัทธ์สะสม

เพื่อให้คุณสามารถดูวิธีการคำนวณความถี่สัมพัทธ์สะสมได้ ตัวอย่างสองตัวอย่างที่แก้ไขทีละขั้นตอนจะแสดงอยู่ด้านล่าง ในตัวอย่างแรก เราค้นหาความถี่สัมพัทธ์สะสมของตัวแปรแยกส่วน และในตัวอย่างที่สองคือตัวแปรต่อเนื่อง เนื่องจากกระบวนการจะแตกต่างกันเล็กน้อย

ตัวอย่างที่ 1: ตัวแปรไม่ต่อเนื่อง

• คะแนนที่ได้รับในวิชาสถิติในชั้นเรียนจำนวน 30 คน มีดังนี้ ความถี่สัมพัทธ์สะสมของแต่ละโน้ตคือเท่าใด

ในกรณีนี้ ตัวแปรจะไม่ต่อเนื่อง เนื่องจากไม่สามารถรับค่าทศนิยมได้ ดังนั้นจึงไม่จำเป็นต้องจัดกลุ่มข้อมูลตามช่วงเวลา แต่สามารถคำนวณได้โดยตรง

ดังนั้นเราจึงจัดทำตารางความถี่และกำหนดความถี่สัมบูรณ์ของแต่ละค่าที่แตกต่างกัน:

ต่อไป เราจะคำนวณความถี่สัมพัทธ์ของแต่ละค่า (คุณสามารถดูวิธีการได้ในลิงก์ที่จุดเริ่มต้นของโพสต์)

และเมื่อเราคำนวณความถี่สัมบูรณ์และความถี่สัมพัทธ์ของชุดข้อมูลแล้ว เราก็จะได้ความถี่สัมพัทธ์สะสม ในการดำเนินการนี้ เราต้องบวกความถี่สัมพัทธ์ของค่าที่ต้องการบวกกับความถี่สัมพัทธ์ก่อนหน้าทั้งหมด หรืออีกนัยหนึ่งคือ ความถี่สัมพัทธ์สะสมก่อนหน้า:

กล่าวโดยสรุป ตารางความถี่ที่มีความถี่สัมบูรณ์ ความถี่สัมพัทธ์ และความถี่สัมพัทธ์สะสมมีดังนี้

โปรดทราบว่าค่าสุดท้ายของความถี่สัมพัทธ์สะสมควรเป็น 1 เสมอ หากคุณได้ตัวเลขอื่น แสดงว่าคำนวณผิดพลาด

ตัวอย่างที่ 2: ตัวแปรต่อเนื่อง

• วัดส่วนสูงจำนวน 20 คน และได้ผลลัพธ์ตามที่ระบุไว้ด้านล่าง แยกข้อมูลออกเป็นช่วงๆ และค้นหาความถี่สัมพัทธ์สะสมของแต่ละช่วง

กรณีนี้แตกต่างจากปัญหาก่อนหน้าเนื่องจากตัวเลขเป็นทศนิยม ซึ่งหมายความว่าตัวแปรสามารถรับค่าใดๆ ก็ได้และต่อเนื่องกัน ดังนั้นเราจะสร้างตารางความถี่โดยการจัดกลุ่มข้อมูลตามช่วงเวลา

ดังนั้นเราจึงสร้างตารางและรับความถี่สัมบูรณ์ของแต่ละช่วงเวลา:

ตอนนี้เราคำนวณความถี่สัมพัทธ์โดยการหารความถี่สัมบูรณ์ของแต่ละช่วงเวลาด้วยจำนวนจุดข้อมูลทั้งหมด:

และสุดท้าย เราก็พบความถี่สัมพัทธ์สะสมของช่วงเวลาทั้งหมด เช่นเดียวกับเมื่อก่อน เพื่อกำหนดความถี่สัมพัทธ์สะสมของช่วงเวลาหนึ่งๆ จำเป็นต้องเพิ่มความถี่สัมพัทธ์ของช่วงเวลาดังกล่าวบวกกับความถี่สัมพัทธ์ก่อนหน้า:

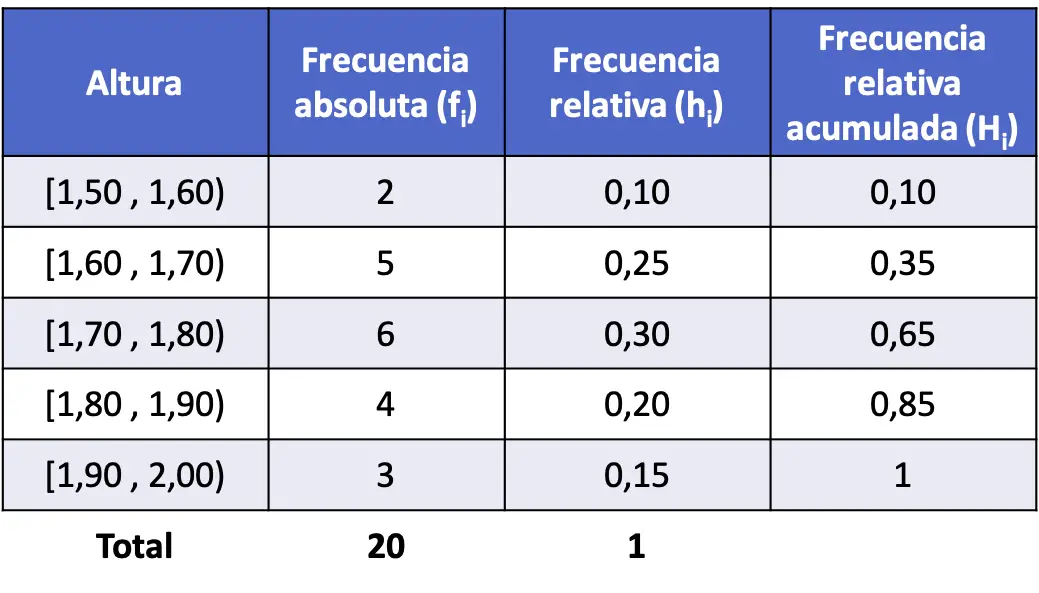
ความถี่สัมพัทธ์สะสมและความถี่สัมบูรณ์สะสม

เราเพิ่งเห็นว่าความถี่สัมพัทธ์สะสมได้มาจากความถี่สัมพัทธ์อย่างไร อย่างไรก็ตาม ความถี่ประเภทนี้สามารถพบได้โดยใช้ความถี่สัมบูรณ์สะสม

ความถี่สัมพัทธ์สะสมสามารถคำนวณได้โดยการหารความถี่สัมบูรณ์สะสมด้วยจำนวนข้อมูลทั้งหมดในตัวอย่าง

ดังนั้น สูตรสำหรับความถี่สัมพัทธ์สะสม คือ:

ทอง:

• 

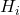
  คือความถี่สัมพัทธ์สะสม

• 

  คือ ความถี่สัมบูรณ์สะสม

• 

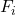
  คือจำนวนข้อมูลทั้งหมด

ตามตัวอย่างแรกที่พัฒนาขึ้นข้างต้น ต่อไปนี้เป็นวิธีค้นหาความถี่สัมพัทธ์สะสมจากความถี่สัมบูรณ์สะสม:

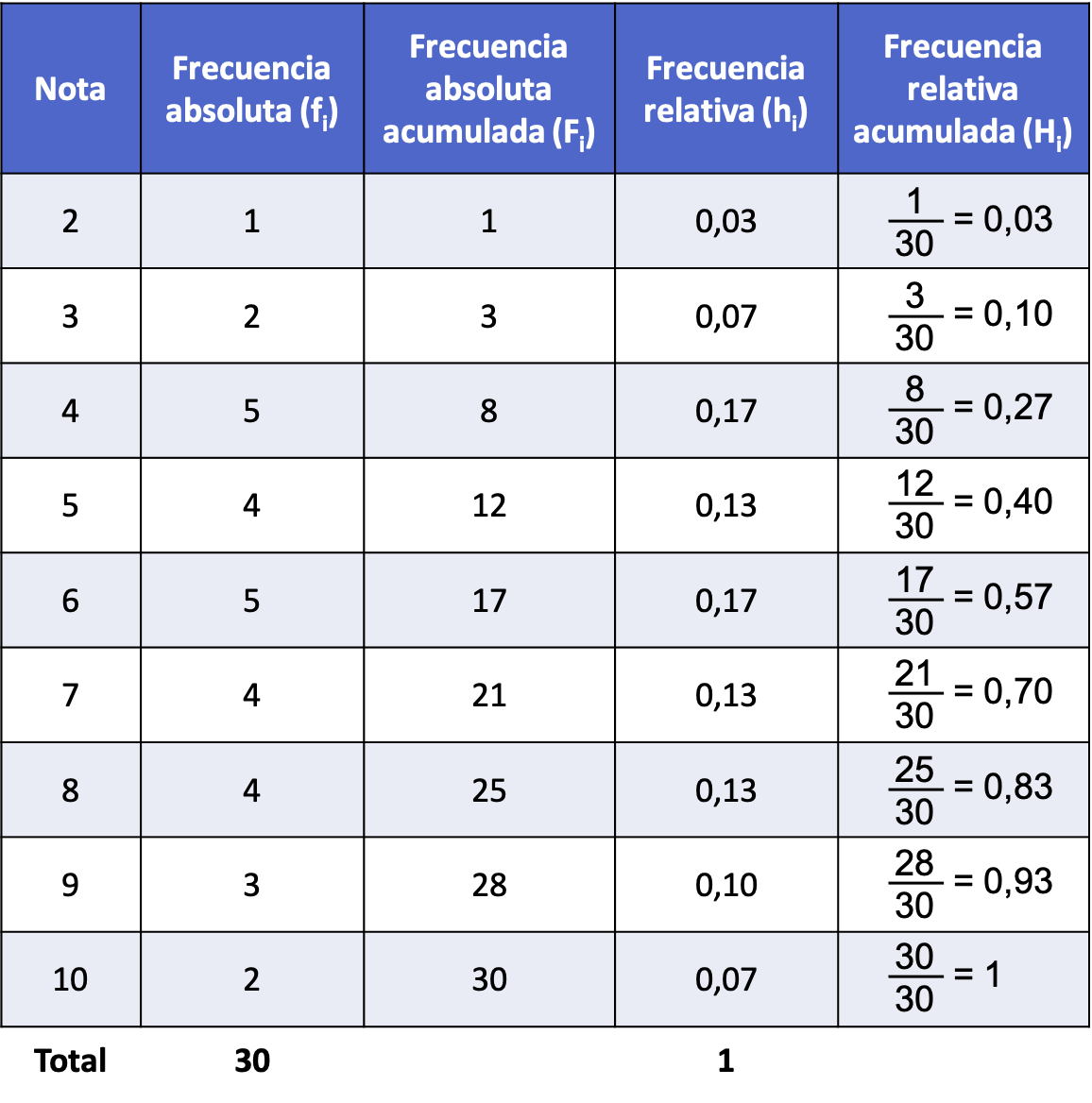
ตารางด้านบนเนื่องจากมีความถี่ทางสถิติทุกประเภท จึงเรียกว่าตารางความถี่ คลิกที่นี่เพื่อหาข้อมูลเพิ่มเติม: