ความน่าจะเป็นที่จุดตัดกันของเหตุการณ์

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 1, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายวิธีคำนวณความน่าจะเป็นที่จุดตัดกันของเหตุการณ์ต่างๆ ดังนั้นคุณจะพบว่าอะไรคือสูตรของความน่าจะเป็นที่จุดตัดของเหตุการณ์และนอกจากนี้แบบฝึกหัดยังแก้ไขได้ทีละขั้นตอน

จุดตัดของเหตุการณ์คืออะไร?

ในทฤษฎีความน่าจะ เป็น จุดตัดของเหตุการณ์ คือการดำเนินการของเหตุการณ์ที่ผลลัพธ์ประกอบด้วยเหตุการณ์เบื้องต้นที่เหมือนกันกับเหตุการณ์ทั้งหมดของการดำเนินการ นั่นคือจุดตัดของเหตุการณ์ A และ B เกิดขึ้นจากเหตุการณ์ทั้งหมดที่เป็นของ A และ B ในเวลาเดียวกัน

จุดตัดของเหตุการณ์ทั้งสองแสดงด้วยสัญลักษณ์ ⋂ ดังนั้น จุดตัดของเหตุการณ์ A และ B จึงเขียนว่า A⋂B

ตัวอย่างเช่น ในการทดลองสุ่มของการทอยลูกเต๋า ถ้าเหตุการณ์หนึ่งคือว่าเลขคู่ถูกทอย A={2, 4, 6} และอีกเหตุการณ์หนึ่งคือว่าเลขที่มากกว่าสามถูกทอย B={4, 5, 6 } จุดตัดของเหตุการณ์ทั้งสองคือ A⋂B={4, 6}

สูตรความน่าจะเป็นที่เหตุการณ์จะตัดกัน

ความน่าจะเป็นที่จุดตัดกันของสองเหตุการณ์ จะเท่ากับความน่าจะเป็นของเหตุการณ์หนึ่งที่เกิดขึ้น คูณความน่าจะเป็นแบบมีเงื่อนไขของอีกเหตุการณ์หนึ่งที่เกิดขึ้นจากเหตุการณ์แรก

ดังนั้น สูตรความน่าจะเป็นที่จุดตัดของเหตุการณ์สองเหตุการณ์ คือ P(A⋂B)=P(A) P(B|A)=P(B) P(A|B)

$P(A\cap B)=P(A)\cdot P(B|A)=P(B)\cdot P(A|B)$

ทอง:

$A$

และ

$B$

นี่เป็นเหตุการณ์ที่ต้องพึ่งพาสองเหตุการณ์
$P(A\cap B)$

คือความน่าจะเป็นที่จุดตัดของเหตุการณ์ A และเหตุการณ์ B
$P(A)$

คือความน่าจะเป็นที่เหตุการณ์ A จะเกิดขึ้น
$P(B|A)$

คือความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ B ที่เกิดขึ้นเมื่อพิจารณาจากเหตุการณ์ A
$P(B)$

คือความน่าจะเป็นที่เหตุการณ์ B จะเกิดขึ้น
$P(A|B)$

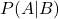
คือความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ A ที่เกิดขึ้นเมื่อพิจารณาจากเหตุการณ์ B

➤ ดู: ความน่าจะเป็นแบบมีเงื่อนไข (หรือ ความน่าจะเป็นแบบมีเงื่อนไข)

อย่างไรก็ตาม หากทั้งสองเหตุการณ์เป็นอิสระต่อกัน หมายความว่าความน่าจะเป็นที่เหตุการณ์หนึ่งจะเกิดขึ้นไม่ได้ขึ้นอยู่กับว่าอีกเหตุการณ์หนึ่งเกิดขึ้นหรือไม่ ดังนั้นสูตรความน่าจะเป็นที่จุดตัดกันของเหตุการณ์อิสระทั้งสองจึงเป็นดังนี้

$P(A\cap B)=P(A)\cdot P(B)$

ทอง:

$A$

และ

$B$

นี่เป็นสองเหตุการณ์ที่เป็นอิสระ
$P(A\cap B)$

คือความน่าจะเป็นที่จุดตัดกันของเหตุการณ์ A และเหตุการณ์ B
$P(A)$

คือความน่าจะเป็นที่เหตุการณ์ A จะเกิดขึ้น
$P(B)$

คือความน่าจะเป็นที่เหตุการณ์ B จะเกิดขึ้น

➤ ดู: กิจกรรมอิสระ

ตัวอย่างความน่าจะเป็นทางแยกของเหตุการณ์ในโลกแห่งความเป็นจริง

ต่อไป เราจะปล่อยตัวอย่างสองตัวอย่างให้คุณแก้ไขทีละขั้นตอน เพื่อให้คุณสามารถดูวิธีการคำนวณความน่าจะเป็นที่จุดตัดกันของเหตุการณ์สองเหตุการณ์ ขั้นแรกเราจะเห็นตัวอย่างของจุดตัดกันของเหตุการณ์อิสระสองเหตุการณ์ จากนั้นจึงเห็นเหตุการณ์ที่ขึ้นต่อกันสองเหตุการณ์ ดังนั้นคุณจึงสามารถเห็นทั้งสองกรณีได้

ความน่าจะเป็นที่จุดตัดกันของเหตุการณ์อิสระสองเหตุการณ์

การจับสลากเกิดขึ้นสามครั้งติดต่อกัน ค้นหาความน่าจะเป็นที่จะได้หัวจากการเสี่ยงทั้งสามครั้ง

ในกรณีนี้ เหตุการณ์ที่เราต้องการคำนวณความน่าจะเป็นร่วมนั้นมีความเป็นอิสระ เนื่องจากผลลัพธ์ของการจับฉลากไม่ได้ขึ้นอยู่กับผลลัพธ์ที่ได้รับในการจับรางวัลครั้งก่อน ดังนั้น เพื่อกำหนดความน่าจะเป็นที่จะได้หัว 3 ครั้งติดต่อกัน เราต้องใช้สูตรความน่าจะเป็นแบบตัดกันสำหรับเหตุการณ์อิสระ:

$P(A\cap B)=P(A)\cdot P(B)$

การออกสลากมีเพียงสองผลลัพธ์เท่านั้นที่เราจะออกหัวหรือก้อยได้ ดังนั้น ความน่าจะเป็นที่จะได้หัวหรือก้อยเมื่อโยนเหรียญคือ:

$P(\text{cara})=\cfrac{1}{2}=0,5$

ดังนั้น เพื่อหาความน่าจะเป็นที่จะได้หัวจากการโยนเหรียญทั้งสามครั้ง เราต้องคูณความน่าจะเป็นที่จะได้หัวด้วยสาม:

$\begin{aligned}P(\text{cara}\cap \text{cara}\cap \text{cara})&=P(\text{cara})\cdot P(\text{cara})\cdot P(\text{cara})\\[2ex]&=0,5\cdot 0,5\cdot 0,5\\[2ex]&=0,125\end{aligned}$

กล่าวโดยสรุป ความน่าจะเป็นที่จะได้หัวสามครั้งติดต่อกันคือ 12.5%

ความน่าจะเป็นที่จุดตัดกันของเหตุการณ์ที่ขึ้นต่อกันสองเหตุการณ์

ในกล่องเปล่าเราใส่ลูกบอลสีน้ำเงิน 8 ลูก ลูกบอลสีส้ม 4 ลูก และลูกบอลสีเขียว 2 ลูก ถ้าเราจั่วลูกแรกแล้วอีกลูกหนึ่งโดยไม่นำลูกแรกที่ดึงกลับเข้าไปในกรอบ ความน่าจะเป็นที่ลูกแรกเป็นสีฟ้าและลูกที่สองสีส้มเป็นเท่าใด

ในกรณีนี้ เหตุการณ์จะขึ้นอยู่กับ เนื่องจากความน่าจะเป็นในการหยิบลูกบอลสีส้มในการจับฉลากครั้งที่สองขึ้นอยู่กับสีของลูกบอลในการจับฉลากครั้งแรก ดังนั้น ในการคำนวณความน่าจะเป็นที่ปัญหาถามเรา เราต้องใช้สูตรความน่าจะเป็นของจุดตัดสำหรับเหตุการณ์ที่ไม่ขึ้นอยู่กับ:

$P(A\cap B)=P(A)\cdot P(B|A)$

ความน่าจะเป็นที่จะได้ลูกบอลสีน้ำเงินในการจับฉลากครั้งแรกนั้นง่ายต่อการกำหนด เพียงหารจำนวนลูกบอลสีน้ำเงินด้วยจำนวนลูกบอลทั้งหมด:

$P(\text{bola azul})=\cfrac{8}{8+4+2}=\cfrac{8}{14}=0,57$

ในทางกลับกัน ความน่าจะเป็นที่จะจั่วลูกบอลสีส้มหลังจากหยิบลูกบอลสีน้ำเงินจะคำนวณแตกต่างกันเนื่องจากจำนวนลูกบอลสีส้มแตกต่างกัน และยิ่งไปกว่านั้น ตอนนี้มีลูกบอลน้อยกว่าหนึ่งลูกในกล่อง:

$P(\text{bola naranja}|\text{bola azul})=\cfrac{4}{7+4+2}=\cfrac{4}{13}=0,31$

ดังนั้น ความน่าจะเป็นที่จะจั่วลูกบอลสีน้ำเงินก่อนแล้วจึงได้ลูกบอลสีส้มจึงคำนวณโดยการคูณความน่าจะเป็นทั้งสองที่พบด้านบน:

$\begin{array}{l}P(\text{bola azul}\cap\text{bola naranja})=\\[2ex]=P(\text{bola azul})\cdot P(\text{bola naranja}|\text{bola azul})=\\[2ex]=0,57\cdot 0,31= \\[2ex]=0,18\end{array}$

➤ ดู: ความน่าจะเป็นของการรวมกันของเหตุการณ์

คุณสมบัติทางแยกเหตุการณ์

ในทฤษฎีความน่าจะเป็น จุดตัดของเหตุการณ์มีคุณสมบัติดังต่อไปนี้

สมบัติการสับเปลี่ยน: ลำดับของเหตุการณ์ทางแยกไม่เปลี่ยนแปลงผลลัพธ์ของการดำเนินการ

$A\cap B=B\cap A$

ทรัพย์สินที่เชื่อมโยง: จุดตัดกันของเหตุการณ์สามเหตุการณ์สามารถคำนวณในลำดับใดก็ได้ เนื่องจากผลลัพธ์จะเหมือนกัน

$(A\cap B)\cap C=A\cap (B\cap C)$

ทรัพย์สินการกระจาย: จุดตัดของเหตุการณ์เป็นไปตามคุณสมบัติการกระจายที่การรวมกันของเหตุการณ์

$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$

➤ ดู: การปฏิบัติการกับเหตุการณ์

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม