ความน่าจะเป็นหลัง: คำจำกัดความ + ตัวอย่าง

ความน่าจะเป็นภายหลัง คือความน่าจะเป็นที่อัปเดตแล้วที่เหตุการณ์จะเกิดขึ้นหลังจากพิจารณาข้อมูลใหม่แล้ว

ตัวอย่างเช่น เราอาจสนใจความน่าจะเป็นที่เหตุการณ์ “A” จะเกิดขึ้นหลังจากการบัญชีสำหรับเหตุการณ์ “B” ที่เพิ่งเกิดขึ้น เราสามารถคำนวณความน่าจะเป็นหลังนี้ได้โดยใช้สูตรต่อไปนี้:

P(A|B) = P(A) * P(B|A) / P(B)

ทอง:

P(A|B) = ความน่าจะเป็นที่เหตุการณ์ A จะเกิดขึ้น เมื่อพิจารณาว่าเหตุการณ์ B เกิดขึ้นแล้ว โปรดทราบว่า “| » หมายถึง “ให้”

P(A) = ความน่าจะเป็นที่เหตุการณ์ A จะเกิดขึ้น

P(B) = ความน่าจะเป็นที่เหตุการณ์ B จะเกิดขึ้น

P(B|A) = ความน่าจะเป็นที่เหตุการณ์ B จะเกิดขึ้น เมื่อพิจารณาว่าเหตุการณ์ A เกิดขึ้นแล้ว

ตัวอย่าง: การคำนวณความน่าจะเป็นภายหลัง

ป่าประกอบด้วยต้นโอ๊ก 20% และเมเปิ้ล 80% สมมติว่าเรารู้ว่าต้นโอ๊ก 90% มีสุขภาพดี ในขณะที่ต้นเมเปิลเพียง 50% เท่านั้นที่มีสุขภาพดี สมมติว่าจากระยะไกล คุณสามารถบอกได้ว่าต้นไม้ต้นใดต้นหนึ่งมีสุขภาพดี ความน่าจะเป็นที่ต้นไม้จะเป็นต้นโอ๊กเป็นเท่าไร?

ระลึกไว้ว่าความน่าจะเป็นที่เหตุการณ์ A จะเกิดขึ้นเมื่อเหตุการณ์ B เกิดขึ้นคือ:

P(A|B) = P(A) * P(B|A) / P(B)

ในตัวอย่างนี้ ความน่าจะเป็นที่ต้นไม้จะเป็นต้นโอ๊กโดยพิจารณาว่าต้นไม้นั้นแข็งแรงดีคือ:

P(โอ๊ค|ดีต่อสุขภาพ) = P(โอ๊ค) * P(ดีต่อสุขภาพ|โอ๊ค) / P(ดีต่อสุขภาพ)

P(Oak) = ความน่าจะเป็นที่ต้นไม้ที่กำหนดเป็นต้นโอ๊กคือ 0.2 เพราะ 20% ของต้นไม้ทั้งหมดในป่าเป็นต้นโอ๊ก

P(Healthy) = ความน่าจะเป็นที่ต้นไม้ที่กำหนดแข็งแรงสามารถคำนวณได้ดังนี้ (0.20)*(0.9) + (0.8)*(0.5) = 0.58

P(Healthy|Oak) = ความน่าจะเป็นที่ต้นไม้มีสุขภาพดีหากเป็นต้นโอ๊กคือ 0.9 เนื่องจากเราได้รับแจ้งว่า 90% ของต้นโอ๊กมีสุขภาพดี

เมื่อใช้ตัวเลขทั้งสามนี้ เราจะสามารถหาความน่าจะเป็นที่ต้นไม้ต้นนั้นจะเป็นต้นโอ๊กเมื่อพิจารณาว่าต้นไม้แข็งแรง:

P(โอ๊ค|ดีต่อสุขภาพ) = P(โอ๊ค) * P(ดีต่อสุขภาพ|โอ๊ค) / P(ดีต่อสุขภาพ) = (0.2) * (0.9) / (0.58) = 0.3103

เพื่อให้เข้าใจถึงความน่าจะเป็นนี้โดยสัญชาตญาณ สมมติว่าตารางต่อไปนี้แสดงถึงป่าที่มีต้นไม้ 100 ต้น ต้นโอ๊ก 20 ต้นและ 18 ต้นมีสุขภาพดี ต้นเมเปิลอีก 80 ต้นและอีก 40 ต้นมีสุขภาพดี

(O = โอ๊ค, M = เมเปิ้ล, เขียว = ดีต่อสุขภาพ, แดง = ไม่ดีต่อสุขภาพ)

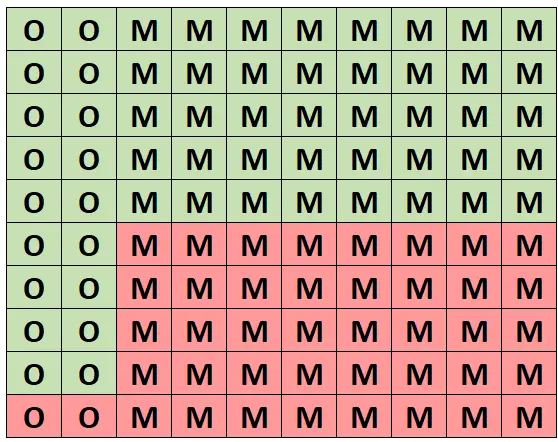
จากต้นไม้ทั้งหมด มี 58 ต้นที่มีสุขภาพดีจริงๆ และ 18 ต้นที่มีสุขภาพดีนั้นเป็นต้นโอ๊ก ดังนั้น หากเรารู้ว่าเราได้เลือกต้นไม้ที่แข็งแรงแล้ว ความน่าจะเป็นที่จะเป็นต้นโอ๊กคือ 18/58 = 0.3103

เมื่อใดที่คุณควรใช้ความน่าจะเป็นภายหลัง

ความน่าจะเป็นภายหลังถูกนำมาใช้ในหลากหลายสาขา รวมถึงการเงิน การแพทย์ เศรษฐศาสตร์ และการพยากรณ์อากาศ

จุดประสงค์ของการใช้ความน่าจะเป็นภายหลังคือการปรับปรุงความเชื่อก่อนหน้านี้ที่เรามีเกี่ยวกับบางสิ่งบางอย่างเมื่อเราได้รับข้อมูลใหม่

จำจากตัวอย่างก่อนหน้านี้ที่เรารู้ว่าความน่าจะเป็นที่ต้นไม้ที่กำหนดในป่าคือต้นโอ๊กคือ 20% สิ่งนี้เรียกว่าความ น่าจะเป็นก่อนหน้า หากเราสุ่มเลือกต้นไม้ต้นหนึ่ง เราก็รู้ว่าความน่าจะเป็นที่ต้นไม้ต้นนั้นจะเท่ากับ 0.20

อย่างไรก็ตาม เมื่อเราได้รับข้อมูลใหม่ว่าต้นไม้ที่เราเลือกนั้นมีสุขภาพดี เราก็สามารถใช้ข้อมูลใหม่นี้เพื่อพิจารณาว่าความ น่าจะเป็นภายหลัง ที่ต้นไม้ต้นนี้จะเป็นต้นโอ๊กคือ 0.3103 แทน

ในโลกแห่งความเป็นจริง ผู้คนค้นพบข้อมูลใหม่ๆ อยู่ตลอดเวลา ข้อมูลใหม่นี้ช่วยให้เราปรับปรุงความเชื่อเดิมของเรา ในแง่สถิติ หมายความว่าเราสามารถสร้างความน่าจะเป็นภายหลังของเหตุการณ์ที่เกิดขึ้น ซึ่งช่วยให้เราเข้าใจโลกได้แม่นยำยิ่งขึ้น และช่วยให้เราคาดการณ์เหตุการณ์ในอนาคตได้แม่นยำยิ่งขึ้น