วิธีสร้างเมทริกซ์ความสับสนใน r (ทีละขั้นตอน)

การถดถอยแบบโลจิสติก เป็นการถดถอยประเภทหนึ่งที่เราสามารถใช้ได้เมื่อตัวแปรตอบสนองเป็นไบนารี

วิธีทั่วไปในการประเมินคุณภาพของแบบจำลองการถดถอยโลจิสติกคือการสร้าง เมทริกซ์ความสับสน ซึ่งเป็นตาราง 2 × 2 ที่แสดงค่าที่คาดการณ์ของแบบจำลองเทียบกับค่าจริงของชุดข้อมูลทดสอบ

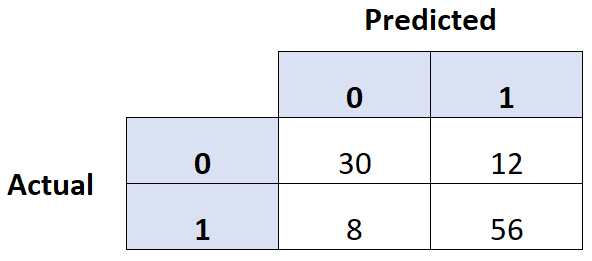
ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีสร้างเมทริกซ์ความสับสนใน R

ขั้นตอนที่ 1: ปรับแบบจำลองการถดถอยโลจิสติก

สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูล เริ่มต้น จากแพ็คเกจ ISLR เราจะใช้สถานะนักศึกษา ยอดคงเหลือในธนาคาร และรายได้ต่อปีเพื่อคาดการณ์แนวโน้มที่บุคคลนั้นจะผิดนัดชำระหนี้เงินกู้

รหัสต่อไปนี้แสดงวิธีปรับแบบจำลองการถดถอยโลจิสติกให้พอดีกับชุดข้อมูลนี้:

 #load necessary packages
library (caret)
library (InformationValue)
library (ISLR)

#load dataset
data <-Default

#split dataset into training and testing set
set. seeds (1)
sample <- sample(c(TRUE, FALSE), nrow(data), replace= TRUE , prob=c(0.7,0.3))
train <- data[sample, ]
test <- data[!sample, ]

#fit logistic regression model
model <- glm(default~student+balance+income, family=" binomial ", data=train)

ขั้นตอนที่ 2: สร้างเมทริกซ์ความสับสน

ต่อไป เราจะใช้ฟังก์ชัน ความสับสนMatrix() จากแพ็คเกจ คาเร็ต เพื่อสร้างเมทริกซ์ความสับสน:

 #use model to predict probability of default
predicted <- predict(model, test, type="response")

#convert defaults from "Yes" and "No" to 1's and 0's
test$default <- ifelse(test$default==" Yes ", 1, 0)

#find optimal cutoff probability to use to maximize accuracy
optimal <- optimalCutoff(test$default, predicted)[1]

#create confusion matrix
confusionMatrix(test$default, predicted)

     0 1
0 2912 64
1 21 39

ขั้นตอนที่ 3: ประเมินเมทริกซ์ความสับสน

นอกจากนี้เรายังสามารถคำนวณหน่วยวัดต่อไปนี้โดยใช้เมทริกซ์ความสับสน:

• ความอ่อนไหว: “อัตราผลบวกที่แท้จริง” – เปอร์เซ็นต์ของบุคคลที่แบบจำลองคาดการณ์อย่างถูกต้องจะเป็นค่าเริ่มต้น
• ความจำเพาะ: “อัตราติดลบที่แท้จริง” – เปอร์เซ็นต์ของบุคคลที่แบบจำลองคาดการณ์อย่างถูกต้องจะ ไม่ เป็นค่าเริ่มต้น
• อัตราการจัดประเภทผิดทั้งหมด: เปอร์เซ็นต์ของการจัดประเภทผิดทั้งหมดที่ทำโดยแบบจำลอง

รหัสต่อไปนี้แสดงวิธีคำนวณหน่วยวัดเหล่านี้:

 #calculate sensitivity
sensitivity(test$default, predicted)

[1] 0.3786408

#calculate specificity
specificity(test$default, predicted)

[1] 0.9928401

#calculate total misclassification error rate
misClassError(test$default, predicted, threshold =optimal)

[1] 0.027

อัตราความผิดพลาดในการจำแนกประเภทรวมคือ 2.7% สำหรับรุ่นนี้

โดยทั่วไป ยิ่งอัตรานี้ต่ำลง โมเดลก็ยิ่งสามารถทำนายผลลัพธ์ได้ดีขึ้นเท่านั้น รูปแบบเฉพาะนี้จึงพิสูจน์ได้ว่ามีประสิทธิภาพมากในการทำนายว่าบุคคลจะผิดนัดชำระหรือไม่