ความสัมพันธ์ลำดับศูนย์คืออะไร?

ในทางสถิติ ความสัมพันธ์ ระหว่างตัวแปรสองตัวบอกเราเกี่ยวกับความสัมพันธ์ระหว่างตัวแปรทั้งสองนี้

ความสัมพันธ์ประเภทพื้นฐานที่สุดประเภทหนึ่งเรียกว่าความ สัมพันธ์แบบลำดับศูนย์ ซึ่งหมายถึงความสัมพันธ์ระหว่างตัวแปรสองตัวโดยไม่ต้องควบคุมอิทธิพลที่เป็นไปได้ของตัวแปรอื่น

ตัวอย่างของความสัมพันธ์ประเภทนี้คือ ค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน ซึ่งวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัวและสามารถรับค่าระหว่าง -1 ถึง 1 โดยที่:

• -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
• 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
• 1 บ่งชี้ความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรสองตัว

ยิ่งความสัมพันธ์เพิ่มเติมจากศูนย์ ความสัมพันธ์ระหว่างตัวแปรทั้งสองก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น

ความสัมพันธ์ลำดับที่หนึ่งและสอง

หากเราคำนวณความสัมพันธ์ระหว่างตัวแปร A และ B สองตัวในขณะที่ควบคุมอิทธิพลของตัวแปร C ตัวที่สาม เราจะเรียกความสัมพันธ์ระหว่าง A และ B ว่าความสัมพันธ์ลำดับที่หนึ่ง

ในทำนองเดียวกัน ถ้าเราคำนวณความสัมพันธ์ระหว่างตัวแปร A และ B สองตัวในขณะที่ควบคุมอิทธิพลของตัวแปร C และ D เราจะเรียกความสัมพันธ์ระหว่าง A และ B ว่าความสัมพันธ์ลำดับที่สอง

ตัวอย่างความสัมพันธ์แบบไม่มีลำดับ

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งแสดงจำนวนชั่วโมงที่ใช้ในการเรียนและเกรดที่นักเรียน 10 คนได้รับจากการสอบ:

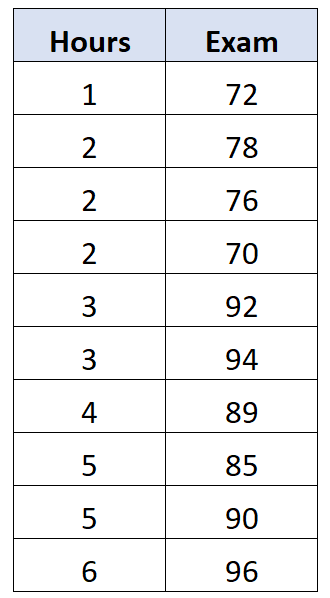
ปรากฎว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองนี้คือ 0.762 . นี่จะถือเป็น ความสัมพันธ์แบบไม่มีลำดับ ระหว่างตัวแปรทั้งสอง เนื่องจากเราไม่ได้ควบคุมอิทธิพลที่อาจเกิดขึ้นของตัวแปรตัวที่สาม

อย่างไรก็ตาม ในความเป็นจริง มีความเป็นไปได้ที่ปัจจัยอื่นๆ จะส่งผลต่อความสัมพันธ์ระหว่างตัวแปรทั้งสองนี้

ตัวอย่างเช่น คะแนนปัจจุบันของนักเรียนในชั้นเรียนอาจส่งผลต่อคะแนนสอบของพวกเขา สมมติว่าเราสามารถเข้าถึงข้อมูลนี้ได้เช่นกัน:

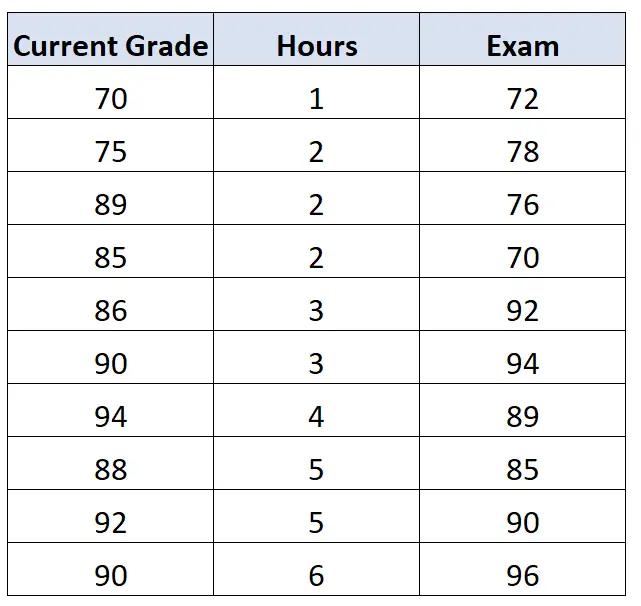
หากเราคำนวณความสัมพันธ์ระหว่างชั่วโมงกับการสอบ โดยควบคุมผลของเกรดปัจจุบัน เราจะพบว่าความ สัมพันธ์อันดับแรก ระหว่างชั่วโมงกับการสอบคือ 0.578

ซึ่งหมายความว่ายังคงมีความสัมพันธ์เชิงบวกที่ค่อนข้างชัดเจนระหว่างชั่วโมงเรียนกับเกรดการสอบ แม้ว่าจะควบคุมผลกระทบของเกรดปัจจุบันของนักเรียนในชั้นเรียนแล้วก็ตาม

หมายเหตุ: ความสัมพันธ์ลำดับที่หนึ่งบางครั้งเรียกว่าความสัมพันธ์บางส่วน บทช่วยสอนนี้ จะอธิบายวิธีการคำนวณความสัมพันธ์บางส่วนใน Excel

ความสัมพันธ์แบบไม่มีลำดับในเมทริกซ์สหสัมพันธ์

เราสร้าง เมทริกซ์สหสัมพันธ์ เมื่อใดก็ตามที่สำหรับชุดของตัวแปร ค่าสัมประสิทธิ์สหสัมพันธ์ที่แสดงในเมทริกซ์จะเป็นความสัมพันธ์แบบไม่มีลำดับเสมอ เพราะเป็นเพียงความสัมพันธ์ระหว่างแต่ละชุดของตัวแปรในทิศทางคู่ โดยไม่คำนึงถึงอิทธิพลของตัวแปรอื่น ๆ

ตัวอย่างเช่น พิจารณาชุดข้อมูลจากตัวอย่างก่อนหน้านี้:

หากเราสร้างเมทริกซ์สหสัมพันธ์สำหรับชุดข้อมูลนี้ จะมีลักษณะดังนี้:

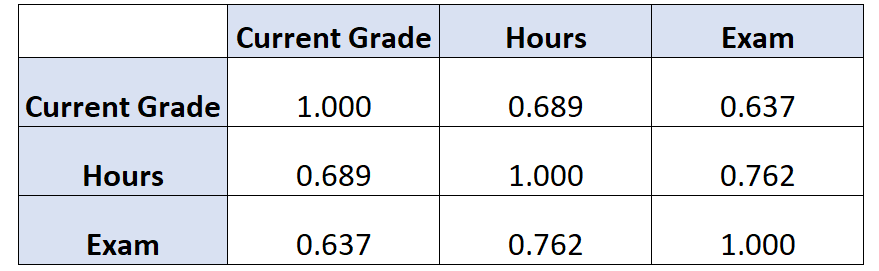
วิธีการตีความนี้คือ:

• ความสัมพันธ์ระหว่างเกรดปัจจุบันกับชั่วโมงเรียนคือ 0.689
• ความสัมพันธ์ระหว่างคะแนนปัจจุบันกับคะแนนที่ได้รับในการสอบคือ 0.637 .
• ความสัมพันธ์ระหว่างชั่วโมงเรียนกับคะแนนสอบเท่ากับ 0.762

แต่ละความสัมพันธ์เหล่านี้เป็น ความสัมพันธ์แบบไม่มีลำดับ

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับค่าสัมประสิทธิ์สหสัมพันธ์:

ความรู้เบื้องต้นเกี่ยวกับสัมประสิทธิ์สหสัมพันธ์เพียร์สัน
วิธีอ่านเมทริกซ์สหสัมพันธ์
วิธีการคำนวณความสัมพันธ์บางส่วนใน Excel