เหตุใดค่ามัธยฐานจึงมีความสำคัญในสถิติ?

ค่ามัธยฐาน แสดงถึงค่ากลางของชุดข้อมูล เมื่อค่าทั้งหมดเรียงลำดับจากน้อยไปหามาก

ตัวอย่างเช่น ค่ามัธยฐานในชุดข้อมูลต่อไปนี้คือ 19:

ชุดข้อมูล: 3, 4, 11, 15, 19 , 22, 23, 23, 26

ค่ามัธยฐานยังแสดงถึงเปอร์เซ็นไทล์ ^{ที่ 50} ของชุดข้อมูลอีกด้วย นั่นคือครึ่งหนึ่งของค่าในชุดข้อมูลนั้นอยู่เหนือค่ามัธยฐานและครึ่งหนึ่งของค่าอยู่ต่ำกว่า

ค่ามัธยฐานเป็นตัวชี้วัดที่สำคัญในการคำนวณเพราะมันช่วยให้เราทราบว่า “ศูนย์กลาง” ของชุดข้อมูลอยู่ที่ไหน นอกจากนี้ยังช่วยให้เราทราบถึงค่า “ทั่วไป” ในชุดข้อมูลที่กำหนด

ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลที่มีราคาขายของบ้านที่แตกต่างกัน 10,000 หลังในเมืองหนึ่งๆ

แทนที่จะดู ข้อมูลดิบ เป็นแถวๆ เราสามารถคำนวณค่ามัธยฐานเพื่อให้เข้าใจราคาขายเฉลี่ยของบ้านในเมืองนั้นได้อย่างรวดเร็ว

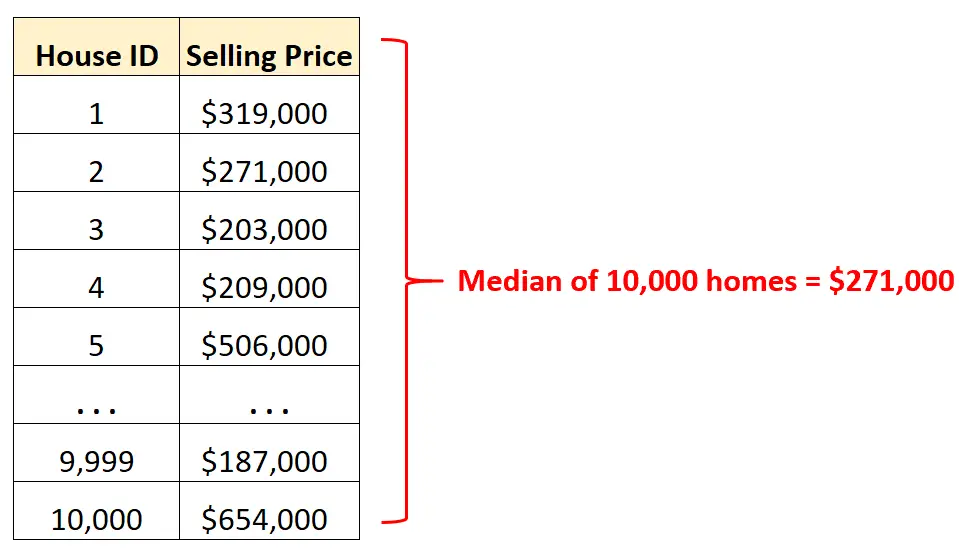
เมื่อรู้ว่าราคาขายเฉลี่ยอยู่ที่ 271,000 ดอลลาร์ เราจึงรู้ว่าบ้านครึ่งหนึ่งของ 10,000 หลังขายได้ในราคาที่มากกว่านั้น และอีกครึ่งหนึ่งขายได้น้อยกว่า

นอกจากนี้ยังช่วยให้เราทราบราคาขาย “ทั่วไป” ของบ้านในเมืองนี้อีกด้วย

เมื่อใดจึงจะใช้ค่ามัธยฐาน

เมื่อวิเคราะห์ชุดข้อมูล เรามักจะต้องการเข้าใจว่าค่ากลางอยู่ที่ใด

ในทางสถิติ มีหน่วยวัดทั่วไปสองหน่วยที่เราใช้ในการวัดศูนย์กลางของชุดข้อมูล:

• Mean : ค่าเฉลี่ยในชุดข้อมูล
• ค่า มัธยฐาน : ค่ามัธยฐานในชุดข้อมูล

ปรากฎว่าค่ามัธยฐานเป็นการวัดที่มีประโยชน์มากกว่าในสถานการณ์ต่อไปนี้:

• เมื่อการกระจาย ตัวไม่สมมาตร
• เมื่อการแจกแจงมีค่าผิดปกติ

เพื่ออธิบายสิ่งนี้ ให้พิจารณาสองตัวอย่างต่อไปนี้

ตัวอย่างที่ 1: การคำนวณค่ามัธยฐานของการแจกแจงแบบเบ้

พิจารณาการกระจายเงินเดือนต่อไปนี้สำหรับผู้อยู่อาศัยในเมืองใดเมืองหนึ่ง:

ค่ามัธยฐานสะท้อนถึงเงินเดือน “ทั่วไป” ของผู้อยู่อาศัยได้ดีกว่าค่าเฉลี่ย เนื่องจากการแจกแจงจะเบ้ไปทางขวา

ซึ่งหมายความว่าค่าจ้างที่สูงทางด้านขวาของการแจกแจงจะผลักค่าเฉลี่ยออกไปจากศูนย์กลางของการแจกแจง

ในตัวอย่างนี้ เงินเดือนโดยเฉลี่ยอยู่ที่ 47,000 เหรียญสหรัฐฯ ในขณะที่เงินเดือนเฉลี่ยอยู่ที่ 32,000 เหรียญสหรัฐฯ ค่ามัธยฐานเป็นตัวแทนของเงินเดือนทั่วไปในเมืองนี้มากกว่ามาก

ตัวอย่างที่ 2: การคำนวณค่ามัธยฐานเมื่อมีค่าผิดปกติ

พิจารณากราฟต่อไปนี้ซึ่งแสดงพื้นที่เป็นตารางฟุตของบ้านบนถนนเส้นหนึ่ง:

ค่าเฉลี่ยได้รับอิทธิพลอย่างมากจากบ้านหลังใหญ่มากบางหลัง ในขณะที่ค่ามัธยฐานไม่ได้รับอิทธิพล

เราจะเห็นว่าค่ามัธยฐานทำงานได้ดีกว่าในการจับภาพพื้นที่เป็นตารางฟุต “ทั่วไป” ของบ้านบนถนนเส้นนั้นมากกว่าค่าเฉลี่ย เนื่องจากไม่ได้รับอิทธิพลจากค่าผิดปกติ

สรุป

นี่เป็นบทสรุปโดยย่อของประเด็นหลักที่กล่าวถึงในบทความนี้:

• ค่ามัธยฐานแสดงถึงค่ากลางในชุดข้อมูล
• ค่ามัธยฐานมีความสำคัญเนื่องจากช่วยให้เราทราบว่าค่ากลางอยู่ที่ใดในชุดข้อมูล
• ค่ามัธยฐานมีแนวโน้มที่จะมีประโยชน์ในการคำนวณมากกว่าค่าเฉลี่ยเมื่อมีการแจกแจงที่เบ้และ/หรือมีค่าผิดปกติ

แหล่งข้อมูลเพิ่มเติม

ตัวอย่างที่เป็นรูปธรรม: การใช้ค่าเฉลี่ย ค่ามัธยฐาน และโหมด
เมื่อใดควรใช้ Mean vs. ค่ามัธยฐาน: พร้อมตัวอย่าง
เหตุใดโหมดจึงมีความสำคัญในสถิติ