เหตุใดค่าเฉลี่ยจึงมีความสำคัญในสถิติ?
ค่า เฉลี่ย ของชุดข้อมูลแสดงถึงค่าเฉลี่ยของชุดข้อมูล มีการคำนวณดังนี้:
ค่าเฉลี่ย = Σx i / n
ทอง:
- Σ: สัญลักษณ์ที่หมายถึง “ผลรวม”
- x i : การสังเกต ครั้งที่ 1 ในชุดข้อมูล
- n: จำนวนการสังเกตทั้งหมดในชุดข้อมูล
ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลต่อไปนี้พร้อมข้อสังเกต 11 รายการ:
ชุดข้อมูล: 3, 4, 4, 6, 7, 8, 12, 13, 15, 16, 17
ค่าเฉลี่ยของชุดข้อมูลคำนวณดังนี้:
ค่าเฉลี่ย = (3+4+4+6+7+8+12+13+15+16+17) / 11 = 9.54
ในทางสถิติ ค่าเฉลี่ยมีความสำคัญด้วยเหตุผลดังต่อไปนี้:
1. ค่าเฉลี่ยช่วยให้เราทราบว่า “ศูนย์กลาง” ของชุดข้อมูลอยู่ที่ไหน
2. เนื่องจากวิธีการคำนวณ ค่าเฉลี่ยจึงมีข้อมูลจาก การสังเกต แต่ละครั้ง ในชุดข้อมูล
ตัวอย่างต่อไปนี้แสดงให้เห็นถึงเหตุผลสองประการนี้
ตัวอย่าง: คำนวณค่าเฉลี่ยของชุดข้อมูล
สมมติว่าเรามีชุดข้อมูลที่มีราคาขายของบ้านที่แตกต่างกัน 10,000 หลังในเมืองหนึ่งๆ

แทนที่จะดู ข้อมูลดิบ หลายพันแถว เราสามารถคำนวณค่าเฉลี่ยเพื่อทำความเข้าใจราคาขายเฉลี่ยของบ้านในเมืองนั้นได้อย่างรวดเร็ว
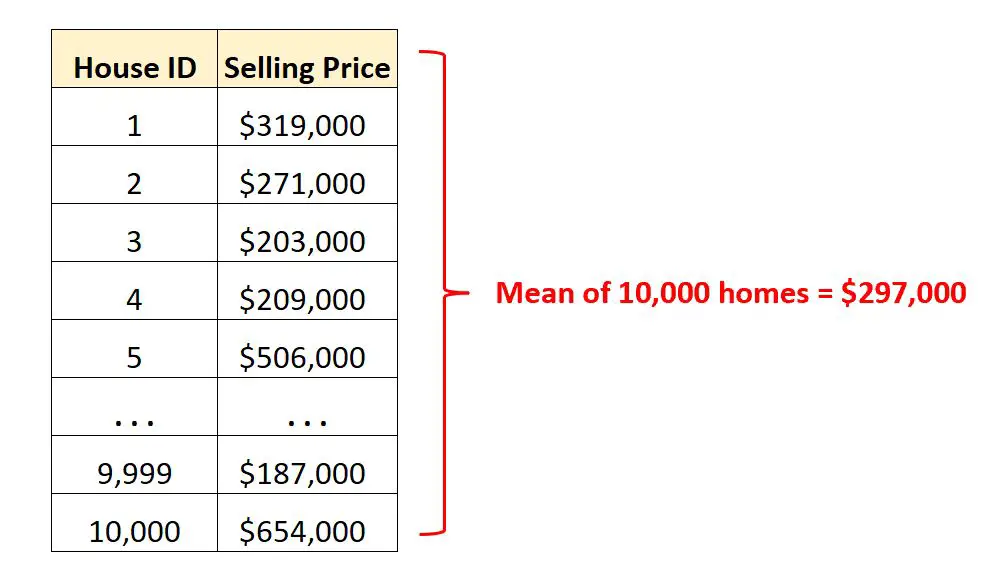
การรู้ว่าราคาขายเฉลี่ยอยู่ที่ 297,000 ดอลลาร์ทำให้เรามีความคิดว่าบ้าน “ทั่วไป” ขายในราคาเท่าใดในเมืองนี้
ค่าเฉลี่ยเพียงค่าเดียวนี้ตีความได้ง่ายกว่าการดูข้อมูลดิบทุกแถว
และเนื่องจากราคาขายบ้านแต่ละหลังถูกนำมาใช้ในการคำนวณค่าเฉลี่ย เราจึงสามารถคูณราคาขายเฉลี่ยด้วยจำนวนบ้านทั้งหมดเพื่อหาราคาขายรวมของบ้านทั้งหมดในเมืองนั้นได้:
- ราคาขายรวมของบ้านทั้งหมด = ราคาขายเฉลี่ย * จำนวนบ้าน
- ราคาขายรวมของบ้านทั้งหมด = 297,000 เหรียญสหรัฐ * 10,000
- ราคาขายรวมของบ้านทั้งหมด = 2,970,000,000 เหรียญสหรัฐ
เราจะเห็นว่าราคาขายรวมของบ้านทั้งหมดในเมืองนี้อยู่ที่ 2.97 พันล้านดอลลาร์
เมื่อใดจึงควรใช้ค่าเฉลี่ย
เมื่อวิเคราะห์ชุดข้อมูล เรามักจะต้องการเข้าใจว่าค่ากลางอยู่ที่ใด
ในทางสถิติ มีหน่วยวัดทั่วไปสองหน่วยที่เราใช้ในการวัดศูนย์กลางของชุดข้อมูล:
- Mean : ค่าเฉลี่ยในชุดข้อมูล
- ค่า มัธยฐาน : ค่ามัธยฐานในชุดข้อมูล
ค่าเฉลี่ยเป็นวิธีที่ใช้กันทั่วไปในการวัดศูนย์กลางของชุดข้อมูล แต่จริงๆ แล้วอาจทำให้เข้าใจผิดได้ในสถานการณ์ต่อไปนี้:
- เมื่อการกระจาย ตัวไม่สมมาตร
- เมื่อการแจกแจงมี ค่าผิดปกติ
เพื่ออธิบายสิ่งนี้ ให้พิจารณาสองตัวอย่างต่อไปนี้
ตัวอย่างที่ 1: การคำนวณค่าเฉลี่ยของการแจกแจงแบบเบ้
พิจารณาการกระจายเงินเดือนต่อไปนี้สำหรับผู้อยู่อาศัยในเมืองใดเมืองหนึ่ง:

ค่าจ้างที่สูงทางด้านขวาของการแจกแจงจะผลักค่าเฉลี่ยออกจากศูนย์กลางของการแจกแจง
ดังนั้นค่ามัธยฐานจึงสะท้อนถึงเงินเดือน “ปกติ” ของผู้อยู่อาศัยได้ดีกว่าค่าเฉลี่ย เนื่องจากการกระจายจะเบ้ไปทางขวา
ในตัวอย่างนี้ เงินเดือนโดยเฉลี่ยอยู่ที่ 47,000 เหรียญสหรัฐฯ ในขณะที่เงินเดือนเฉลี่ยอยู่ที่ 32,000 เหรียญสหรัฐฯ
ดังนั้นค่ามัธยฐานจึงเป็นตัวแทนของเงินเดือนทั่วไปในเมืองนั้นมากกว่ามาก
ตัวอย่างที่ 2: การคำนวณค่าเฉลี่ยเมื่อมีค่าผิดปกติ
พิจารณากราฟต่อไปนี้ซึ่งแสดงพื้นที่เป็นตารางฟุตของบ้านบนถนนเส้นหนึ่ง:

ค่าเฉลี่ยได้รับอิทธิพลอย่างมากจากบ้านหลังใหญ่มากบางหลัง ในขณะที่ค่ามัธยฐานไม่ได้รับอิทธิพล
เราจะเห็นว่าค่ามัธยฐานทำงานได้ดีกว่าในการจับภาพพื้นที่เป็นตารางฟุต “ทั่วไป” ของบ้านบนถนนเส้นนั้นมากกว่าค่าเฉลี่ย เนื่องจากไม่ได้รับอิทธิพลจากค่าผิดปกติ
สรุป
นี่เป็นบทสรุปโดยย่อเกี่ยวกับประเด็นหลักจากบทความนี้:
- ค่าเฉลี่ยแสดงถึงค่าเฉลี่ยในชุดข้อมูล
- ค่าเฉลี่ยมีความสำคัญเนื่องจากช่วยให้เราทราบว่าค่ากลางอยู่ที่ใดในชุดข้อมูล
- ค่าเฉลี่ยก็มีความสำคัญเช่นกันเนื่องจากมีข้อมูลจากการสังเกต แต่ละครั้ง ในชุดข้อมูล
- ค่าเฉลี่ยอาจทำให้เข้าใจผิดได้เมื่อชุดข้อมูลบิดเบี้ยวหรือมีค่าผิดปกติ ในสถานการณ์เหล่านี้ ค่ามัธยฐานจะให้แนวคิดที่แม่นยำมากขึ้นว่า “ศูนย์กลาง” ของชุดข้อมูลอยู่ที่ไหน
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับสถิติเชิงพรรณนาอื่นๆ:
เหตุใดค่ามัธยฐานจึงมีความสำคัญในสถิติ?
เหตุใดค่าเบี่ยงเบนมาตรฐานจึงมีความสำคัญในสถิติ
เมื่อใดควรใช้ค่าเฉลี่ยกับค่ามัธยฐาน