ความแตกต่างปานกลาง

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าค่าเบี่ยงเบนเฉลี่ยคืออะไรและคำนวณอย่างไร นอกจากนี้คุณยังจะพบตัวอย่างที่เป็นรูปธรรมของการคำนวณค่าเบี่ยงเบนเฉลี่ย และยิ่งกว่านั้น คุณจะสามารถคำนวณค่าเบี่ยงเบนเฉลี่ยของชุดข้อมูลทางสถิติใดๆ ได้โดยใช้เครื่องคิดเลขออนไลน์

ค่าเบี่ยงเบนเฉลี่ยคืออะไร?

ค่าเบี่ยงเบนเฉลี่ย หรือที่เรียกว่า ค่าเบี่ยงเบนเฉลี่ยสัมบูรณ์ เป็นการวัดการกระจายตัวทางสถิติ

ค่าเบี่ยงเบนเฉลี่ยของชุดข้อมูลคือค่าเฉลี่ยของค่าเบี่ยงเบนสัมบูรณ์ ดังนั้นค่าเบี่ยงเบนเฉลี่ยจึงเท่ากับผลรวมของการเบี่ยงเบนของแต่ละรายการข้อมูลจากค่าเฉลี่ยเลขคณิตหารด้วยจำนวนรายการข้อมูลทั้งหมด

กล่าวอีกนัยหนึ่ง สูตรสำหรับส่วนเบี่ยงเบนเฉลี่ย มีดังนี้:

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณค่าเบี่ยงเบนเฉลี่ยของชุดข้อมูลใดก็ได้

ในสถิติ ค่าเบี่ยงเบนเฉลี่ยเรียกอีกอย่างว่า ค่าเบี่ยงเบนสัมบูรณ์เฉลี่ย

การตีความค่าเบี่ยงเบนเฉลี่ยทำได้ดังนี้ ยิ่งค่าเบี่ยงเบนเฉลี่ยมีค่ามากขึ้น หมายความว่าข้อมูลโดยเฉลี่ยอยู่ไกลจากค่าเฉลี่ยเลขคณิต ในทางกลับกัน ยิ่งค่าเบี่ยงเบนเฉลี่ยต่ำ ค่าก็จะยิ่งใกล้มากขึ้น ข้อมูลคือ ค่าเบี่ยงเบนเฉลี่ยจึงบ่งชี้ถึงการกระจายตัวของชุดข้อมูล

การวัดอื่นๆ ที่ถือว่ามีการกระจาย ได้แก่ พิสัย พิสัยระหว่างควอร์ไทล์ ค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนมาตรฐาน) ความแปรปรวน และสัมประสิทธิ์ของการแปรผัน

วิธีการคำนวณส่วนเบี่ยงเบนเฉลี่ย

ในการคำนวณค่าเบี่ยงเบนเฉลี่ยของชุดข้อมูล ต้องปฏิบัติตามขั้นตอนต่อไปนี้:

คำนวณค่าเฉลี่ยเลขคณิต ของชุดข้อมูลทางสถิติ
คำนวณค่าเบี่ยงเบนของแต่ละจุดข้อมูลจากค่าเฉลี่ย ซึ่งกำหนดเป็นค่าสัมบูรณ์ของความแตกต่างระหว่างข้อมูลกับค่าเฉลี่ย
รวมผลต่างทั้งหมดที่คำนวณในขั้นตอนก่อนหน้า
หารด้วยจำนวนข้อมูลทั้งหมด ผลลัพธ์ที่ได้คือค่าเบี่ยงเบนเฉลี่ยของชุดข้อมูล

โดยสรุปสูตรที่ต้องใช้ในการหาค่าเบี่ยงเบนเฉลี่ยคือ

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

ตัวอย่างการคำนวณค่าเบี่ยงเบนเฉลี่ย

เมื่อพิจารณาคำจำกัดความของค่าเบี่ยงเบนเฉลี่ย ด้านล่างนี้คือตัวอย่างการคำนวณค่าเบี่ยงเบนเฉลี่ยของตัวอย่างทางสถิติที่ได้รับการแก้ไขทีละขั้นตอน วิธีนี้จะทำให้คุณเข้าใจวิธีหาค่าเบี่ยงเบนเฉลี่ยได้ดีขึ้น

นักวิเคราะห์ศึกษาผลลัพธ์ทางเศรษฐกิจของบริษัทในปีที่ผ่านมา และมีข้อมูลเกี่ยวกับผลกำไรที่บริษัทได้รับในแต่ละไตรมาสของปีดังกล่าว: 2, 3, 7 และ 5 ล้านดอลลาร์ ค่าเบี่ยงเบนเฉลี่ยของข้อมูลคือเท่าไร?

ขั้นแรก เราต้องหาค่าเฉลี่ยของข้อมูล จากนั้นจึงบวกและหารด้วยจำนวนข้อสังเกตทั้งหมด (4):

$\overline{x}=\cfrac{2+3+7+5}{4}=4,25$

เมื่อเราคำนวณค่าเฉลี่ยเลขคณิตแล้ว เราจะใช้สูตรส่วนเบี่ยงเบนค่าเฉลี่ย:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

เราแทนที่ข้อมูลลงในสูตร:

$D_{\overline{x}}=\cfrac{|2-4,25|+|3-4,25|+|7-4,25|+|5-4,25|}{4}$

เราทำการคำนวณในตัวเศษ:

$D_{\overline{x}}=\cfrac{|-2,25|+|-1,25|+|2,75|+|0,75|}{4}$

$D_{\overline{x}}=\cfrac{2,25+1,25+2,75+0,75}{4}$

$D_{\overline{x}}=\cfrac{7}{4}$

และสุดท้าย เราหารด้วยจำนวนข้อมูลทั้งหมดเพื่อให้ได้ค่าเบี่ยงเบนเฉลี่ยของกลุ่มตัวอย่าง:

$D_{\overline{x}}=1,75$

เครื่องคำนวณค่าเบี่ยงเบนเฉลี่ย

ป้อนชุดข้อมูลทางสถิติลงในเครื่องคิดเลขต่อไปนี้เพื่อคำนวณค่าเบี่ยงเบนเฉลี่ย ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

ค่าเบี่ยงเบนเฉลี่ยสำหรับข้อมูลที่จัดกลุ่ม

ในการคำนวณค่าเบี่ยงเบนเฉลี่ยของข้อมูลที่จัดกลุ่มตามช่วงเวลา ต้องปฏิบัติตามขั้นตอนต่อไปนี้:

หาค่าเฉลี่ยเลขคณิตของชุดข้อมูลทางสถิติ เนื่องจากข้อมูลถูกจัดกลุ่ม นิพจน์ในการคำนวณค่าเฉลี่ยคือ:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}$

คำนวณค่าเบี่ยงเบนของแต่ละช่วงจากค่าเฉลี่ย ซึ่งเท่ากับค่าสัมบูรณ์ของผลต่างระหว่างเกรดของชั้นเรียนกับค่าเฉลี่ย

$|x_i-\overline{x}|$

คูณค่าเบี่ยงเบนของแต่ละช่วงเวลาด้วยความถี่สัมบูรณ์

$|x_i-\overline{x}|\cdot f_i$

รวมผลลัพธ์ทั้งหมดจากขั้นตอนก่อนหน้า จากนั้นหารด้วยจำนวนข้อมูลทั้งหมด ผลลัพธ์ที่ได้คือค่าเบี่ยงเบนเฉลี่ยของกลุ่มตัวอย่างที่จัดกลุ่มตามช่วงต่างๆ

$\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

โดยสรุป สูตรการหาค่าเบี่ยงเบนเฉลี่ยจากข้อมูลที่จัดกลุ่ม คือ

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

เมื่อมีการจัดกลุ่มข้อมูล มักจะหมายความว่ามีข้อมูลจำนวนมาก และการค้นหาค่าเบี่ยงเบนเฉลี่ยนั้นมีหลายขั้นตอน ดังนั้นจึงมักใช้ตารางความถี่ในการคำนวณ

ด้านล่างนี้คือแบบฝึกหัดทีละขั้นตอนเกี่ยวกับวิธีคำนวณค่าเบี่ยงเบนเฉลี่ยเมื่อข้อมูลถูกจัดกลุ่มตามช่วงเวลา:

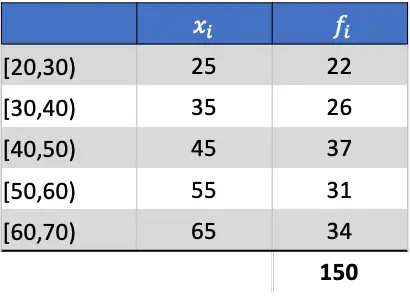
สิ่งแรกที่ต้องทำคือการคำนวณค่าเฉลี่ยของข้อมูลที่จัดกลุ่ม เมื่อต้องการทำเช่นนี้ เราจะเพิ่มคอลัมน์ลงในตารางโดยการคูณบันทึกย่อของชั้นเรียนด้วยความถี่:

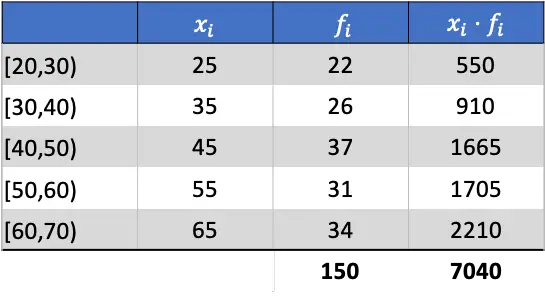
ค่าเฉลี่ยเลขคณิตจึงเป็นผลมาจากการหารผลรวมของคอลัมน์ที่บวกด้วยผลรวมของความถี่สัมบูรณ์:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}=\cfrac{7040}{150}=46,93$

ตอนนี้เราทราบค่าเฉลี่ยของข้อมูลแล้ว เราก็สามารถเพิ่มคอลัมน์ที่จำเป็นทั้งหมดเพื่อค้นหาค่าเบี่ยงเบนเฉลี่ยได้:

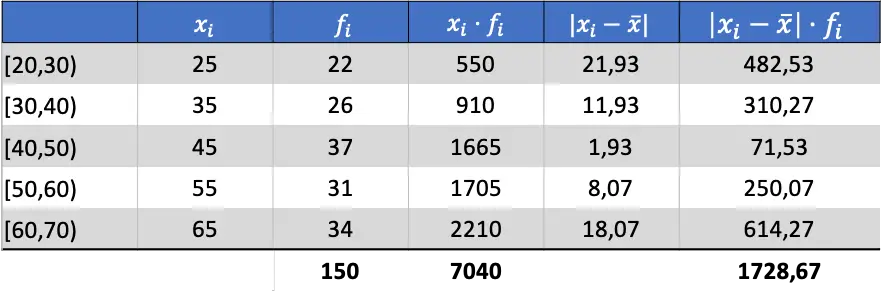
ดังนั้น เพื่อให้ได้ค่าเบี่ยงเบนเฉลี่ย คุณต้องหารผลรวมของคอลัมน์สุดท้ายด้วยจำนวนการสังเกตทั้งหมด:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}=\cfrac{1728,67}{150}=11,52$

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม