ความแปรปรวน
ในบทความนี้ เราจะอธิบายว่าความแปรปรวนหรือที่เรียกว่าความแปรปรวนคืออะไร และวิธีการคำนวณ คุณจะพบกับสูตรความแปรปรวน ซึ่งเป็นตัวอย่างที่ชัดเจนของการคำนวณความแปรปรวน และนอกจากนี้ คุณจะสามารถคำนวณความแปรปรวนของชุดข้อมูลใดๆ ด้วยเครื่องคิดเลขออนไลน์ได้
นอกจากนี้เรายังแสดงวิธีค้นหาความแปรปรวนของข้อมูลที่จัดกลุ่มด้วย เนื่องจากวิธีนี้ใช้วิธีอื่น สุดท้ายนี้ เราจะสอนคุณถึงความแตกต่างระหว่างความแปรปรวนประชากรและความแปรปรวนตัวอย่าง ความแตกต่างระหว่างความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน และคุณสมบัติของการวัดทางสถิตินี้
ความแปรปรวนคืออะไร?
ในสถิติ ความแปรปรวนคือการวัดการกระจายตัวซึ่งบ่งชี้ถึงความแปรปรวนของตัวแปรสุ่ม ความแปรปรวนเท่ากับผลรวมของกำลังสองของส่วนที่เหลือหารด้วยจำนวนการสังเกตทั้งหมด
โปรดทราบว่าส่วนที่เหลือเข้าใจว่าเป็นความแตกต่างระหว่างค่าของจุดข้อมูลทางสถิติและค่าเฉลี่ยของชุดข้อมูล
ในทฤษฎีความน่าจะเป็น สัญลักษณ์ของความแปรปรวนคืออักษรกรีกซิกมากำลังสอง (σ 2 ) แม้ว่าโดยปกติจะแสดงเป็น Var(X) โดยที่ X เป็นตัวแปรสุ่มที่ใช้คำนวณความแปรปรวน
โดยทั่วไป การตีความค่าความแปรปรวนของตัวแปรสุ่ม นั้นทำได้ง่าย ยิ่งค่าความแปรปรวนมากขึ้น ข้อมูลก็จะยิ่งกระจัดกระจายมากขึ้น และในทางกลับกัน ยิ่งค่าความแปรปรวนน้อยลง การกระจายตัวในชุดข้อมูลก็จะยิ่งน้อยลง อย่างไรก็ตาม เมื่อตีความความแปรปรวน เราต้องระวังค่า ผิดปกติ เนื่องจากค่าเหล่านี้สามารถบิดเบือนค่าความแปรปรวนได้
ความแปรปรวน การวัดอื่นๆ ที่พิจารณานอกเหนือจากการกระจายตัว ได้แก่ พิสัย ส่วนเบี่ยงเบนมาตรฐาน ส่วนเบี่ยงเบนเฉลี่ย และสัมประสิทธิ์ของการแปรผัน
วิธีการคำนวณช่องว่าง
ในการคำนวณผลต่าง ต้องดำเนินการขั้นตอนต่อไปนี้:
- ค้นหา ค่าเฉลี่ยเลขคณิต ของชุดข้อมูล
- คำนวณค่าคงเหลือโดยกำหนดเป็นส่วนต่างระหว่างค่ากับค่าเฉลี่ยของชุดข้อมูล
- ยกกำลังสองแต่ละส่วนที่เหลือ
- เพิ่มผลลัพธ์ทั้งหมดที่คำนวณในขั้นตอนก่อนหน้า
- หารด้วยจำนวนข้อมูลทั้งหมด ผลลัพธ์ที่ได้คือความแปรปรวนของชุดข้อมูล
โดยสรุป สูตรในการคำนวณความแปรปรวน ของชุดข้อมูลคือ:

ทอง:
-

คือตัวแปรสุ่มที่คุณต้องการคำนวณความแปรปรวน
-

คือค่าข้อมูล

.
-

คือจำนวนการสังเกตทั้งหมด
-

คือค่าเฉลี่ยของตัวแปรสุ่ม

.
👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณความแปรปรวนของชุดข้อมูลใดก็ได้
ดังนั้น หากต้องการแยกความแปรปรวนออกจากชุดข้อมูล จำเป็นอย่างยิ่งที่คุณจะต้องรู้วิธีคำนวณค่าเฉลี่ยเลขคณิต หากคุณจำไม่ได้ว่าต้องทำอย่างไร คุณสามารถดูได้ในบทความตามลิงก์ด้านบน
ตัวอย่างของการเบี่ยงเบน
ตอนนี้เรารู้คำจำกัดความของความแปรปรวนแล้ว เราจะแก้แบบฝึกหัดทีละขั้นตอนเพื่อให้คุณเห็นว่าได้รับความแปรปรวนของชุดข้อมูลได้อย่างไร
- จากบริษัทข้ามชาติ ทราบผลลัพธ์ทางเศรษฐกิจในช่วงห้าปีที่ผ่านมา โดยส่วนใหญ่ได้รับผลกำไร แต่หนึ่งปีกลับขาดทุนอย่างมาก: 11.5, 2, -9, 7 ล้านยูโร คำนวณความแปรปรวนของชุดข้อมูลนี้
ตามที่เราเห็นในคำอธิบายข้างต้น สิ่งแรกที่เราต้องทำเพื่อค้นหาความแปรปรวนของชุดข้อมูลคือการคำนวณค่าเฉลี่ยเลขคณิต:
![]()
และเมื่อเรารู้ค่าเฉลี่ยของข้อมูลแล้ว เราก็สามารถใช้สูตรความแปรปรวนได้:

เราแทนที่ข้อมูลที่ให้ไว้ในคำสั่งการฝึกหัดลงในสูตร:
![]()
สุดท้าย สิ่งที่เหลืออยู่คือการแก้ปัญหาการดำเนินการเพื่อคำนวณความแปรปรวน:
![Rendered by QuickLaTeX.com \begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c2cbee60d77f19e88117e1bcf28d9cb2_l3.png)
โปรดทราบว่าหน่วยความแปรปรวนเป็นหน่วยเดียวกันกับข้อมูลทางสถิติแต่เป็นหน่วยกำลังสอง ด้วยเหตุนี้ ความแปรปรวนของกลุ่มข้อมูลนี้จึงเท่ากับ 45.76 ล้านยูโร 2
เครื่องคิดเลขช่องว่าง
ป้อนข้อมูลทางสถิติลงในเครื่องคำนวณต่อไปนี้เพื่อคำนวณความแปรปรวน ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม
ความแปรปรวนของข้อมูลที่จัดกลุ่ม
ในการคำนวณความแปรปรวนของข้อมูลที่จัดกลุ่มตามช่วงเวลา ต้องปฏิบัติตามขั้นตอนต่อไปนี้:
- ค้นหาค่าเฉลี่ยของข้อมูลที่จัดกลุ่ม
- คำนวณค่าคงเหลือของข้อมูลที่จัดกลุ่ม
- ยกกำลังสองแต่ละส่วนที่เหลือ
- คูณผลลัพธ์ก่อนหน้าแต่ละรายการด้วยความถี่ของช่วงเวลา
- เพิ่มผลรวมของค่าทั้งหมดที่ได้รับในขั้นตอนก่อนหน้า
- หารด้วยจำนวนการสังเกตทั้งหมด จำนวนผลลัพธ์คือความแปรปรวนของข้อมูลที่จัดกลุ่ม
กล่าวอีกนัยหนึ่ง สูตรในการคำนวณความแปรปรวนของข้อมูลที่จัดกลุ่มตามช่วงเวลามีดังนี้
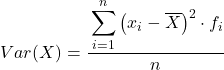
แม้ว่าปกติจะใช้สูตรข้างต้น แต่นิพจน์พีชคณิตด้านล่างก็สามารถนำมาใช้ได้เนื่องจากเทียบเท่ากัน:
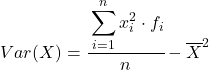
ตามตัวอย่าง เราจะค้นหาความแปรปรวนของชุดข้อมูลที่จัดกลุ่มต่อไปนี้:
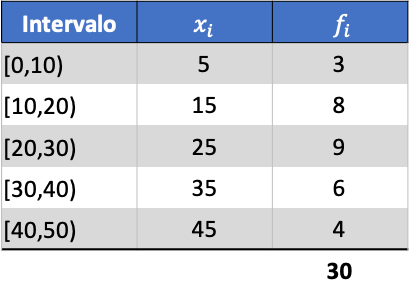
อันดับแรก เราต้องกำหนดค่าเฉลี่ยของข้อมูลที่จัดกลุ่มก่อน เมื่อต้องการทำเช่นนี้ เราเพิ่มคอลัมน์ในตารางความถี่ด้วยผลคูณของเครื่องหมายคลาสและความถี่:
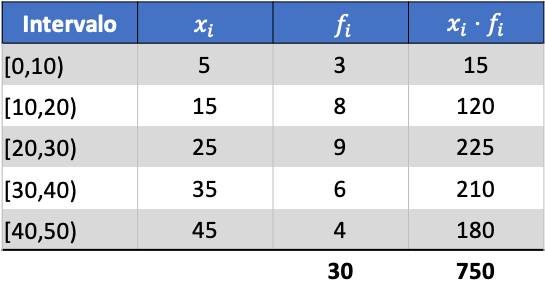
ตอนนี้เราคำนวณค่าเฉลี่ยของข้อมูลที่จัดกลุ่มโดยการหารผลรวมของคอลัมน์ที่เพิ่มด้วยจำนวนข้อมูลทั้งหมด:
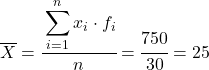
และจากค่าเฉลี่ยของข้อมูลที่คำนวณ เราสามารถบวกสามคอลัมน์ต่อไปนี้:
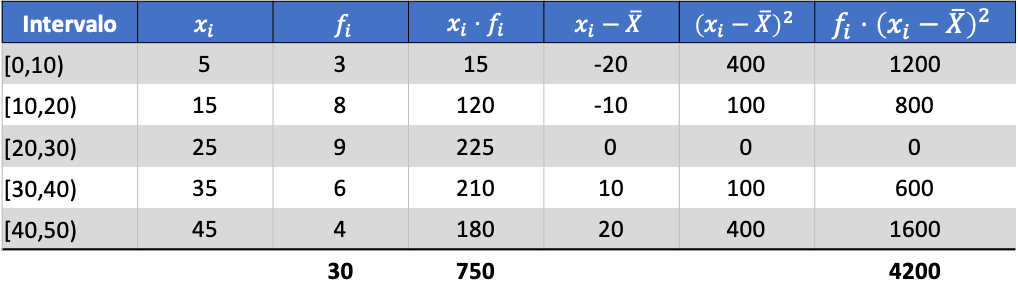
ดังนั้นความแปรปรวนของชุดข้อมูลที่รวบรวมไว้คือผลรวมของคอลัมน์สุดท้ายหารด้วยจำนวนข้อมูลที่สังเกตได้ทั้งหมด:
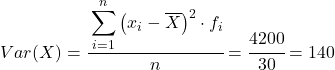
ความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน
ความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน (หรือส่วนเบี่ยงเบนมาตรฐาน) เป็นตัววัดการกระจายตัวสองค่า ดังนั้น ทั้งสองค่าจึงบ่งบอกถึงระดับการกระจายตัวของชุดข้อมูล อย่างไรก็ตาม ความแตกต่างระหว่างความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน ก็คือ ความแปรปรวนทั่วไปมีค่ามากกว่า เนื่องจากมันคือกำลังสองของส่วนเบี่ยงเบนมาตรฐาน
โดยทั่วไปค่าเบี่ยงเบนมาตรฐานจะแสดงด้วยอักษรกรีกซิกมา (σ) และด้วยเหตุนี้ ความแปรปรวนจึงแสดงด้วยตัวอักษรซิกมากำลังสอง (σ 2 ) เนื่องจากเป็นความสัมพันธ์ทางคณิตศาสตร์ที่มีอยู่ระหว่างหน่วยเมตริกการกระจายตัวทั้งสองนี้
![]()
ดังนั้น เมื่อคุณคำนวณค่าความแปรปรวนของชุดข้อมูลแล้ว คุณสามารถค้นหาค่าเบี่ยงเบนมาตรฐานของชุดเดียวกันนั้นได้อย่างง่ายดายโดยการหารากที่สองของความแปรปรวน
![]()
ความแปรปรวนของประชากรและความแปรปรวนตัวอย่าง
ตามหลักเหตุผล ความแปรปรวนประชากร หมายถึงการคำนวณความแปรปรวนของประชากรทางสถิติ และใช้ ความแปรปรวนตัวอย่าง ในการคำนวณความแปรปรวนของกลุ่มตัวอย่างแทน อย่างไรก็ตาม นี่เป็นแนวคิดที่แตกต่างกันสองแนวคิด เนื่องจากสูตรความแปรปรวนประชากรแตกต่างจากสูตรความแปรปรวนตัวอย่าง
โดยปกติในแบบฝึกหัดความแปรปรวน หากพวกเขาไม่ได้บอกเราเป็นอย่างอื่น เพื่อค้นหาความแปรปรวนของชุดข้อมูลที่ให้ไว้ เราต้องใช้ สูตรความแปรปรวนประชากร ซึ่งเป็นสูตรที่เราอธิบายไว้ตอนต้นของบทความ:
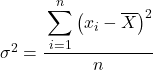
แต่บางทีในบางปัญหา ระบบจะขอให้คุณปฏิบัติต่อข้อมูลทางสถิติเป็นตัวอย่าง ซึ่งในกรณีนี้ เราจำเป็นต้องใช้ สูตรความแปรปรวนตัวอย่าง :
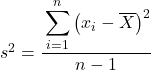
โปรดทราบว่าเพื่อระบุว่ากำลังคำนวณความแปรปรวนของประชากร จะมีการระบุด้วยตัวอักษรกรีก σ แต่เมื่อคำนวณความแปรปรวนตัวอย่าง จะใช้ตัวอักษร s
ดังที่คุณเห็น ข้อแตกต่างเพียงอย่างเดียวระหว่างสองสูตรคือในความแปรปรวนของกลุ่มตัวอย่าง เราต้องหารด้วยจำนวนการสังเกตทั้งหมดลบ 1 เช่น หากมีทั้งหมด 30 รายการข้อมูล เราจะหารด้วย 29 แต่การคำนวณตัวเศษก็ทำในลักษณะเดียวกันทุกประการ
คุณสมบัติความแปรปรวน
ความแปรปรวนมีคุณสมบัติดังต่อไปนี้:
- ความแปรปรวนของตัวแปรสุ่มใดๆ ก็ตามจะมากกว่าหรือเท่ากับศูนย์เสมอ ในทำนองเดียวกัน หากความแปรปรวนเป็นศูนย์ หมายความว่าข้อมูลทางสถิติทั้งหมดเหมือนกัน
![]()
- แน่นอนว่าความแปรปรวนของค่าเดียวจะเป็นศูนย์
![]()
- ความแปรปรวนของผลคูณของสเกลาร์ต่อตัวแปรจะเท่ากับสเกลาร์กำลังสองคูณกับความแปรปรวนของตัวแปร
![]()
- ความแปรปรวนของผลรวมของตัวแปรตามสองตัวเทียบเท่ากับผลรวมของความแปรปรวนของตัวแปรแต่ละตัวแยกกัน บวกสองเท่าของความแปรปรวนร่วมระหว่างตัวแปรทั้งสอง
![]()
- ดังนั้น หากตัวแปรทั้งสองเป็นอิสระต่อกัน เพื่อพิจารณาความแปรปรวนของผลรวม ก็เพียงพอที่จะบวกค่าความแปรปรวนเข้าด้วยกัน:
![]()
- ค่าเบี่ยงเบนสามารถกำหนดได้ด้วยความคาดหวังทางคณิตศาสตร์โดยใช้สูตรต่อไปนี้:
![]()