ช่องว่างที่เหลือคืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)

ความแปรปรวนคงเหลือ (บางครั้งเรียกว่า “ความแปรปรวนที่ไม่สามารถอธิบายได้”) หมายถึงความแปรปรวนในแบบจำลองที่ไม่สามารถอธิบายได้ด้วยตัวแปรแบบจำลอง

ยิ่งความแปรปรวนคงเหลือของแบบจำลองสูงเท่าใด แบบจำลองก็จะยิ่งสามารถอธิบายความแปรผันของข้อมูลได้น้อยลงเท่านั้น

ความแปรปรวนคงเหลือปรากฏในผลลัพธ์ของแบบจำลองทางสถิติที่แตกต่างกันสองแบบ:

1. ANOVA: ใช้เพื่อเปรียบเทียบค่าเฉลี่ยของกลุ่มอิสระตั้งแต่ 3 กลุ่มขึ้นไป

2. การถดถอย: ใช้เพื่อหาปริมาณความสัมพันธ์ระหว่างตัวแปรทำนายตั้งแต่หนึ่งตัวขึ้นไปและ ตัวแปรตอบสนอง

ตัวอย่างต่อไปนี้แสดงวิธีตีความความแปรปรวนคงเหลือในแต่ละวิธีเหล่านี้

ความแปรปรวนคงเหลือในแบบจำลอง ANOVA

ทุกครั้งที่เราปรับโมเดล ANOVA (“การวิเคราะห์ความแปรปรวน”) ให้เหมาะสม เราจะได้ตาราง ANOVA ที่มีลักษณะดังนี้:

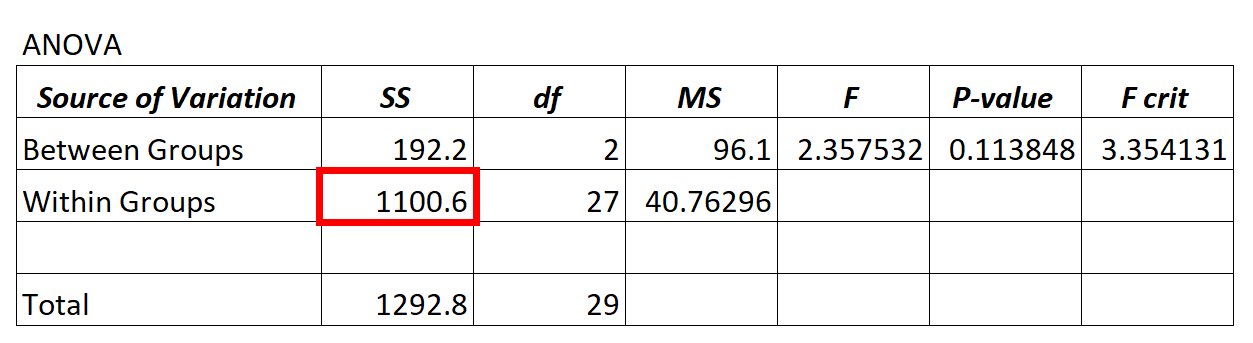
ค่าความแปรปรวนคงเหลือจากแบบจำลอง ANOVA จะอยู่ในคอลัมน์ SS (“ผลรวมของกำลังสอง”) สำหรับการแปรผัน ภายในกลุ่ม

ค่านี้เรียกอีกอย่างว่า “ผลรวมของข้อผิดพลาดกำลังสอง” และคำนวณโดยใช้สูตรต่อไปนี้:

Σ(X _ij – X _j ) ²

ทอง:

• Σ : สัญลักษณ์กรีกหมายถึง “ผลรวม”
• X _ij : การสังเกต ^{ครั้งที่ 3} ของกลุ่ม j
• X _j : ค่าเฉลี่ยของกลุ่ม j

ในแบบจำลอง ANOVA ข้างต้น เราจะเห็นว่าความแปรปรวนที่เหลือคือ 1100.6

เพื่อตรวจสอบว่าความแปรปรวนที่เหลือนี้ “สูง” หรือไม่ เราสามารถคำนวณผลรวมเฉลี่ยของกำลังสองสำหรับภายในกลุ่มและผลรวมเฉลี่ยของกำลังสองสำหรับระหว่างกลุ่ม แล้วค้นหาอัตราส่วนระหว่างทั้งสอง ซึ่งให้ค่า F โดยรวมในตาราง ANOVA

• F = MS _เข้า / MS _เข้า
• ฟ = 96.1 / 40.76296
• เอฟ = 2.357

ค่า F ในตาราง ANOVA ด้านบนคือ 2.357 และค่า p ที่สอดคล้องกันคือ 0.113848 เนื่องจากค่า p นี้ไม่น้อยกว่า α = 0.05 เราจึงไม่มีหลักฐานเพียงพอที่จะปฏิเสธสมมติฐานว่าง

ซึ่งหมายความว่าเราไม่มีหลักฐานเพียงพอที่จะบอกว่าความแตกต่างเฉลี่ยระหว่างกลุ่มที่เรากำลังเปรียบเทียบนั้นแตกต่างกันอย่างมีนัยสำคัญ

สิ่งนี้บอกเราว่าความแปรปรวนที่เหลือของแบบจำลอง ANOVA นั้นสูงเมื่อเทียบกับความแปรปรวนที่แบบจำลองสามารถอธิบายได้จริง

ความแปรปรวนคงเหลือในแบบจำลองการถดถอย

ในแบบจำลองการถดถอย ความแปรปรวนที่เหลือถูกกำหนดเป็นผลรวมของกำลังสองของความแตกต่างระหว่างจุดข้อมูลที่คาดการณ์ไว้และจุดข้อมูลที่สังเกตได้

มีการคำนวณดังนี้:

Σ(ŷ _ฉัน – _ฉัน ) ²

ทอง:

• Σ : สัญลักษณ์กรีกหมายถึง “ผลรวม”
• ŷ _i : จุดข้อมูลที่คาดการณ์
• y _i : จุดข้อมูลที่สังเกตได้

เมื่อเราพอดีกับแบบจำลองการถดถอย เรามักจะได้รับผลลัพธ์ที่มีลักษณะดังนี้:

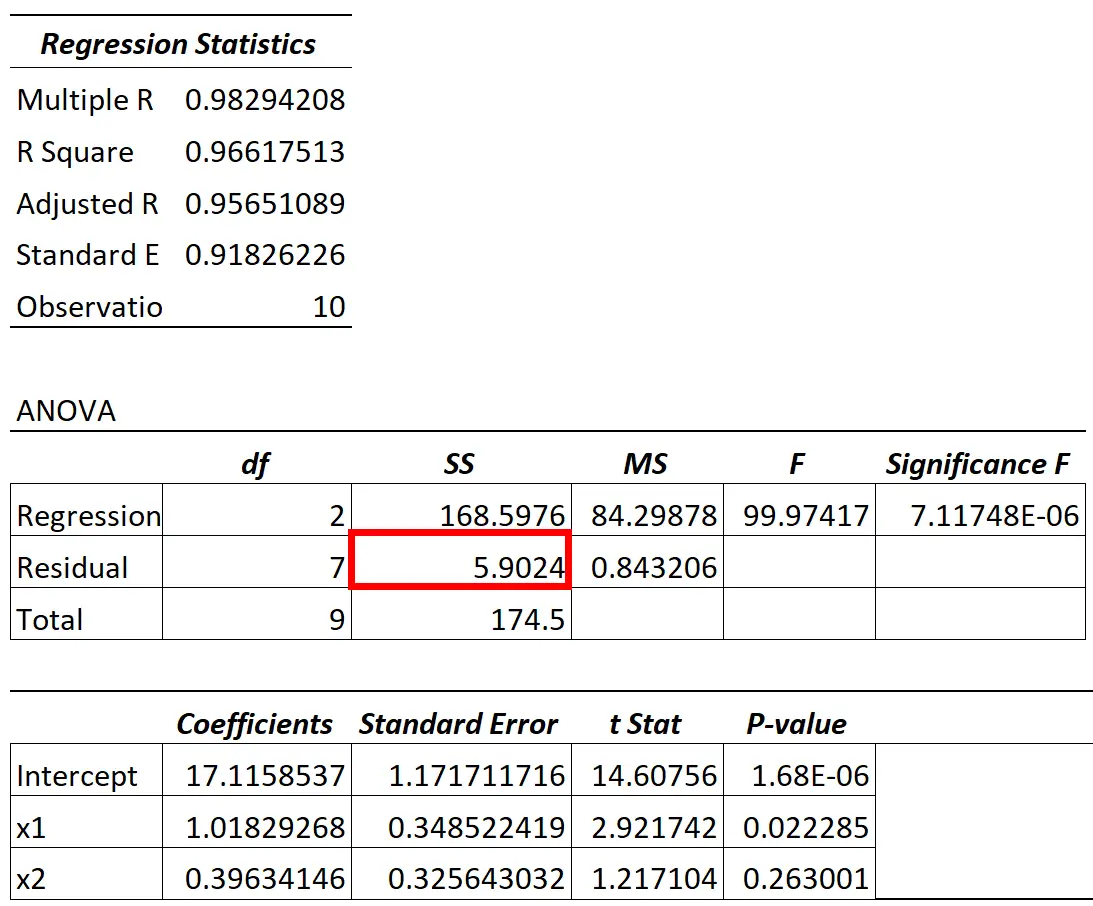
ค่าความแปรปรวนคงเหลือจากแบบจำลอง ANOVA สามารถพบได้ในคอลัมน์ SS (“ผลรวมของกำลังสอง”) สำหรับการแปรผันของค่าคงเหลือ

อัตราส่วนของความแปรผันที่เหลือต่อความแปรผันทั้งหมดในแบบจำลองบอกเราถึงเปอร์เซ็นต์ของความแปรผันในตัวแปรตอบสนองที่ตัวแปรทำนายในแบบจำลองไม่สามารถอธิบายได้

ตัวอย่างเช่น ในตารางด้านบน เราจะคำนวณเปอร์เซ็นต์ดังนี้:

• ความแปรผันที่ไม่สามารถอธิบายได้ = SS Residual / SS Total
• ความแปรผันที่ไม่สามารถอธิบายได้ = 5.9024 / 174.5
• ความแปรผันที่ไม่สามารถอธิบายได้ = 0.0338

ค่านี้สามารถคำนวณได้โดยใช้สูตรต่อไปนี้:

• ความแปรผันที่ไม่สามารถอธิบายได้ = 1 – R ²
• ความแปรผันที่ไม่สามารถอธิบายได้ = 1 – 0.96617
• ความแปรผันที่ไม่สามารถอธิบายได้ = 0.0338

ค่า R-squared ของแบบจำลองบอกเราถึงเปอร์เซ็นต์ของการแปรผันในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรทำนาย

ดังนั้น ยิ่งความแปรผันที่ไม่สามารถอธิบายได้ต่ำลง โมเดลก็ยิ่งมีความสามารถมากขึ้นในการใช้ตัวแปรทำนายเพื่ออธิบายความแปรผันในตัวแปรตอบสนอง

แหล่งข้อมูลเพิ่มเติม

ค่า R-กำลังสองที่ดีคืออะไร?
วิธีการคำนวณ R-squared ใน Excel
วิธีการคำนวณ R-squared ใน R