ความแปรปรวนสามารถเป็นลบได้หรือไม่?

ในสถิติ คำ ว่าความแปรปรวน หมายถึงวิธีการกระจายค่าในชุดข้อมูลที่กำหนด

คำถามทั่วไปที่นักเรียนถามเกี่ยวกับความแปรปรวนคือ:

ความแปรปรวนสามารถเป็นลบได้หรือไม่?

คำตอบ: ไม่ ความแปรปรวนไม่สามารถเป็นลบได้ ค่าต่ำสุดที่สามารถรับได้คือศูนย์

เพื่อให้เข้าใจว่าเหตุใดจึงเป็นเช่นนี้ เราต้องเข้าใจว่าแท้จริงแล้วมีการคำนวณความแปรปรวนอย่างไร

วิธีการคำนวณช่องว่าง

สูตรการหาความแปรปรวนของกลุ่มตัวอย่าง (แทนด้วย s ² ) คือ:

s ² = Σ (x _i – x ) ² / (n-1)

ทอง:

• x : หมายถึงตัวอย่าง
• x _i : การสังเกต ^{ครั้งที่ 3} ในกลุ่มตัวอย่าง
• N : ขนาดตัวอย่าง
• Σ : สัญลักษณ์กรีกหมายถึง “ผลรวม”

ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งมี 10 ค่า:

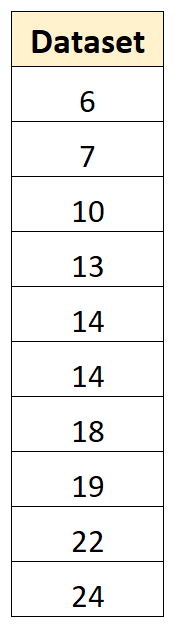
เราสามารถใช้ขั้นตอนต่อไปนี้เพื่อคำนวณความแปรปรวนของตัวอย่างนี้:

ขั้นตอนที่ 1: ค้นหาค่าเฉลี่ย

ค่าเฉลี่ยเป็นเพียงค่าเฉลี่ย นี่กลายเป็น 14.7 .

ขั้นตอนที่ 2: ค้นหาส่วนเบี่ยงเบนกำลังสอง

จากนั้นเราสามารถคำนวณค่าเบี่ยงเบนกำลังสองของแต่ละค่าจากค่าเฉลี่ยได้

ตัวอย่างเช่น ค่าเบี่ยงเบนกำลังสองแรกคำนวณเป็น (6-14.7) ² = 75.69

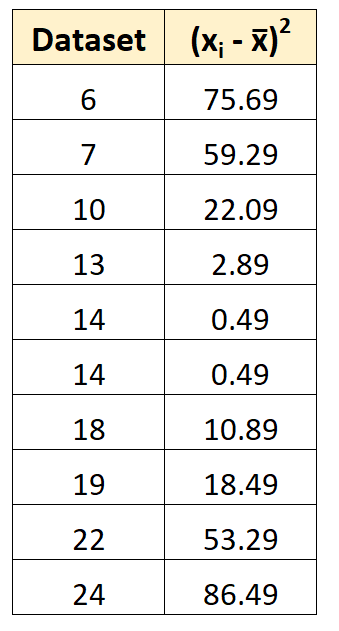
ขั้นตอนที่ 3: ค้นหาผลรวมของการเบี่ยงเบนกำลังสอง

จากนั้นเราสามารถรวมกำลังสองของการเบี่ยงเบนทั้งหมดได้:

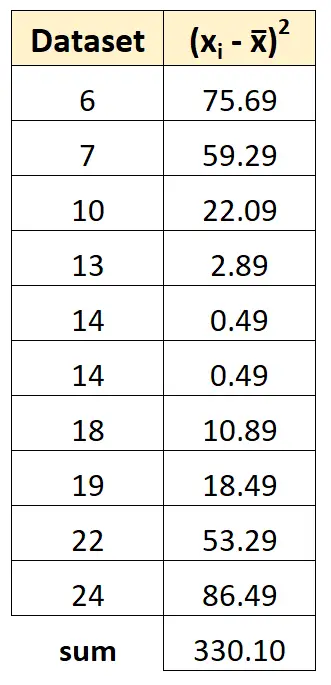
ขั้นตอนที่ 4: คำนวณความแปรปรวนตัวอย่าง

สุดท้ายนี้ เราสามารถคำนวณความแปรปรวนตัวอย่างเป็นผลรวมของส่วนเบี่ยงเบนกำลังสองหารด้วย (n-1):

ส ² = 330.1 / (10-1) = 330.1 / 9 = 36.678

ความแปรปรวนตัวอย่างกลายเป็น 36,678

ตัวอย่างของความแปรปรวนเป็นศูนย์

วิธีเดียวที่ชุดข้อมูลจะมีความแปรปรวนเป็นศูนย์คือถ้า ค่าทั้งหมดในชุดข้อมูลเหมือนกัน

ตัวอย่างเช่น ชุดข้อมูลต่อไปนี้มีความแปรปรวนตัวอย่างเป็นศูนย์:

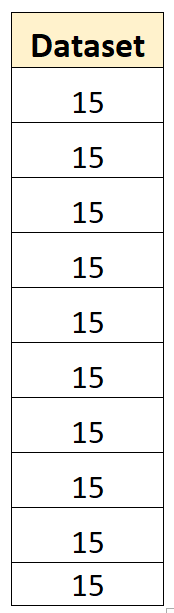
ค่าเฉลี่ยของชุดข้อมูลคือ 15 และไม่มีค่าใดเบี่ยงเบนไปจากค่าเฉลี่ย ดังนั้น ผลรวมของกำลังสองของการเบี่ยงเบนจะเป็นศูนย์ และความแปรปรวนตัวอย่างจะเป็นศูนย์

ค่าเบี่ยงเบนมาตรฐานสามารถเป็นลบได้หรือไม่?

วิธีทั่วไปในการวัดการกระจายของค่าในชุดข้อมูลคือการใช้ค่าเบี่ยงเบนมาตรฐาน ซึ่งเป็นเพียงรากที่สองของความแปรปรวน

ตัวอย่างเช่น หากความแปรปรวนของกลุ่มตัวอย่างที่กำหนดคือ ^s2 = 36.678 ค่าเบี่ยงเบนมาตรฐาน (เขียนเป็น s ) จะถูกคำนวณดังนี้:

ส = √ ^s2 = √ 36.678 = 6.056

เนื่องจากเรารู้แล้วว่าความแปรปรวนเป็นศูนย์หรือเป็นจำนวนบวกเสมอ ซึ่งหมายความว่า ค่าเบี่ยงเบนมาตรฐานไม่สามารถเป็นลบได้ เนื่องจาก รากที่สองของศูนย์หรือจำนวนบวกไม่สามารถเป็นลบได้

แหล่งข้อมูลเพิ่มเติม

การวัดแนวโน้มส่วนกลาง: คำจำกัดความและตัวอย่าง
มาตรการการกระจายตัว: คำจำกัดความและตัวอย่าง