ความแม่นยำที่สมดุลคืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)

ความแม่นยำที่สมดุล เป็นตัวชี้วัดที่เราสามารถใช้เพื่อประเมินประสิทธิภาพของ แบบจำลองการจำแนกประเภท

มีการคำนวณดังนี้:

ความแม่นยำที่สมดุล = (ความไว + ความเฉพาะเจาะจง) / 2

ทอง:

• ความไว : “อัตราบวกที่แท้จริง” – เปอร์เซ็นต์ของกรณีและปัญหาเชิงบวกที่แบบจำลองสามารถตรวจจับได้
• ความจำเพาะ : “อัตราเชิงลบที่แท้จริง” – เปอร์เซ็นต์ของกรณีและปัญหาเชิงลบที่แบบจำลองสามารถตรวจพบได้

หน่วยวัดนี้มีประโยชน์อย่างยิ่งเมื่อทั้งสองคลาสไม่สมดุล กล่าวคือ คลาสหนึ่งปรากฏมากกว่าคลาสอื่นมาก

ตัวอย่างต่อไปนี้แสดงวิธีคำนวณความแม่นยำที่สมดุลในทางปฏิบัติ และแสดงให้เห็นว่าเหตุใดจึงเป็นหน่วยวัดที่มีประโยชน์

ตัวอย่าง: การคำนวณความแม่นยำที่สมดุล

สมมติว่านักวิเคราะห์กีฬาใช้ แบบจำลองการถดถอยลอจิสติกส์ เพื่อคาดการณ์ว่าผู้เล่นบาสเกตบอลระดับวิทยาลัยกว่า 400 คนจะถูกคัดเลือกเข้าสู่ NBA หรือไม่

เมทริกซ์ความสับสนต่อไปนี้สรุปการคาดการณ์ที่ทำโดยโมเดล:

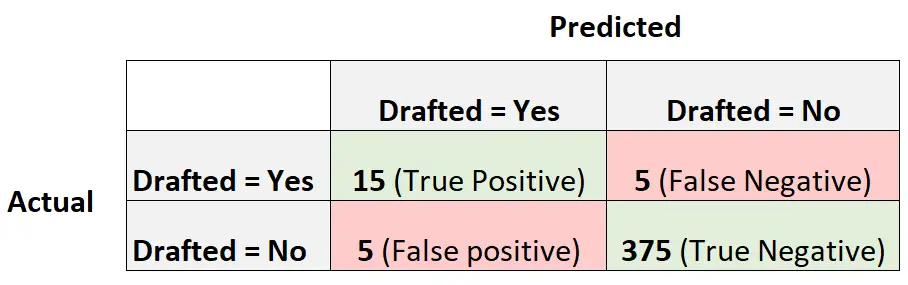
ในการคำนวณความแม่นยำที่สมดุลของแบบจำลอง เราจะคำนวณความไวและความจำเพาะก่อน:

• ความไว : “อัตราบวกที่แท้จริง” = 15 / (15 + 5) = 0.75
• ความจำเพาะ : “อัตราติดลบที่แท้จริง” = 375 / (375 + 5) = 0.9868

จากนั้นเราสามารถคำนวณความแม่นยำที่สมดุลได้ดังนี้:

• ความแม่นยำที่สมดุล = (ความไว + ความเฉพาะเจาะจง) / 2
• ความแม่นยำที่สมดุล = (0.75 + 9868) / 2
• ความแม่นยำที่สมดุล = 0.8684

ความแม่นยำที่สมดุลของแบบจำลองกลายเป็น 0.8684 .

โปรดทราบว่ายิ่งความแม่นยำสมดุลเข้าใกล้ 1 มากเท่าไร โมเดลก็ยิ่งสามารถจำแนกประเภทการสังเกตได้อย่างถูกต้องมากขึ้นเท่านั้น

ในตัวอย่างนี้ ความแม่นยำที่สมดุลค่อนข้างสูง ซึ่งบอกเราว่าแบบจำลองการถดถอยโลจิสติกทำงานได้ดีมากในการทำนายว่าผู้เล่นระดับวิทยาลัยจะถูกร่างเข้าสู่ NBA หรือไม่

ในสถานการณ์นี้ เนื่องจากคลาสไม่สมดุลมาก (ผู้เล่น 20 คนถูกดราฟท์ และผู้เล่น 380 คนไม่ได้ร่าง) ความแม่นยำที่สมดุลทำให้เราเห็นภาพประสิทธิภาพของโมเดลที่สมจริงมากขึ้น เมื่อเปรียบเทียบกับการวัดความแม่นยำโดยรวม

ตัวอย่างเช่น เราจะคำนวณความแม่นยำของโมเดลดังนี้:

• ความแม่นยำ = (TP + TN) / (TP + TN + FP + FN)
• ความแม่นยำ = (15 + 375) / (15 + 375 + 5 + 5)
• ความแม่นยำ = 0.975

ความแม่นยำของโมเดลคือ 0.975 ซึ่งถือว่าสูงมาก

อย่างไรก็ตาม ให้พิจารณาแบบจำลองที่คาดการณ์ว่าผู้เล่นทุกคนจะยังไม่ได้ดราฟต์ จะมีความแม่นยำ 380/400 = 0.95 ซึ่งต่ำกว่าความแม่นยำของโมเดลของเราเพียงเล็กน้อยเท่านั้น

คะแนนความแม่นยำที่สมดุลที่ 0.8684 ช่วยให้เรามีความคิดที่ดีขึ้นเกี่ยวกับความสามารถของแบบจำลองในการทำนายทั้งสองคลาส

กล่าวอีกนัยหนึ่ง มันทำให้เรามีความคิดที่ดีขึ้นเกี่ยวกับความสามารถของโมเดลในการคาดเดาว่าผู้เล่นคนไหนจะยังไม่ได้ร่าง และ ใครจะไป

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีสร้างเมทริกซ์ความสับสนในซอฟต์แวร์ทางสถิติต่างๆ:

วิธีสร้างเมทริกซ์ความสับสนใน Excel
วิธีสร้างเมทริกซ์ความสับสนใน R
วิธีสร้างเมทริกซ์ความสับสนใน Python