วิธีการคำนวณความเบ้และความโด่งใน r

ในสถิติ ความเบ้ และ ความโด่ง เป็นสองวิธีในการวัดรูปร่างของการแจกแจง

ความเบ้ คือการวัดความเบ้ของการแจกแจง ค่านี้สามารถเป็นบวกหรือลบได้

• ความเบ้เชิงลบบ่งชี้ว่าส่วนท้ายอยู่ทางด้านซ้ายของการแจกแจง ซึ่งขยายไปสู่ค่าลบมากขึ้น
• การเอียงเชิงบวกบ่งชี้ว่าส่วนท้ายอยู่ทางด้านขวาของการแจกแจง ซึ่งขยายไปสู่ค่าบวกมากขึ้น
• ค่าศูนย์บ่งชี้ว่าไม่มีความไม่สมดุลในการแจกแจง ซึ่งหมายความว่าการแจกแจงมีความสมมาตรอย่างสมบูรณ์

Kurtosis เป็นตัววัดว่าการกระจายแบบหนักหรือแบบหางเบาเมื่อเทียบกับ การกระจายแบบปกติ

• ความโด่งของการแจกแจงแบบปกติคือ 3
• หากการแจกแจงแบบใดแบบหนึ่งมีความโด่งน้อยกว่า 3 ก็เรียกว่า แบบเพลย์เคิร์ก ซึ่งหมายความว่ามีแนวโน้มที่จะสร้างค่าผิดปกติที่รุนแรงน้อยลงและน้อยลงกว่าการแจกแจงแบบปกติ
• หากการกระจายแบบใดแบบหนึ่งมีความโด่งมากกว่า 3 ก็เรียกว่าเป็น โรคเลปโตเคอร์ติก ซึ่งหมายความว่ามีแนวโน้มที่จะสร้างค่าผิดปกติมากกว่าการกระจายแบบปกติ

หมายเหตุ: บางสูตร (คำจำกัดความของฟิชเชอร์) ลบ 3 ออกจากความโด่งเพื่อให้ง่ายต่อการเปรียบเทียบกับการแจกแจงแบบปกติ เมื่อใช้คำจำกัดความนี้ การแจกแจงจะมีความโด่งมากกว่าการแจกแจงแบบปกติ หากมีค่าความโด่งมากกว่า 0

บทช่วยสอนนี้จะอธิบายวิธีคำนวณทั้งความเบ้และความโด่งของชุดข้อมูลที่กำหนดใน R

ตัวอย่าง: ความเบ้และความแบนใน R

สมมติว่าเรามีชุดข้อมูลต่อไปนี้:

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

เราสามารถมองเห็นการกระจายของค่าในชุดข้อมูลนี้ได้อย่างรวดเร็วโดยการสร้างฮิสโตแกรม:

 hist(data, col=' steelblue ') 

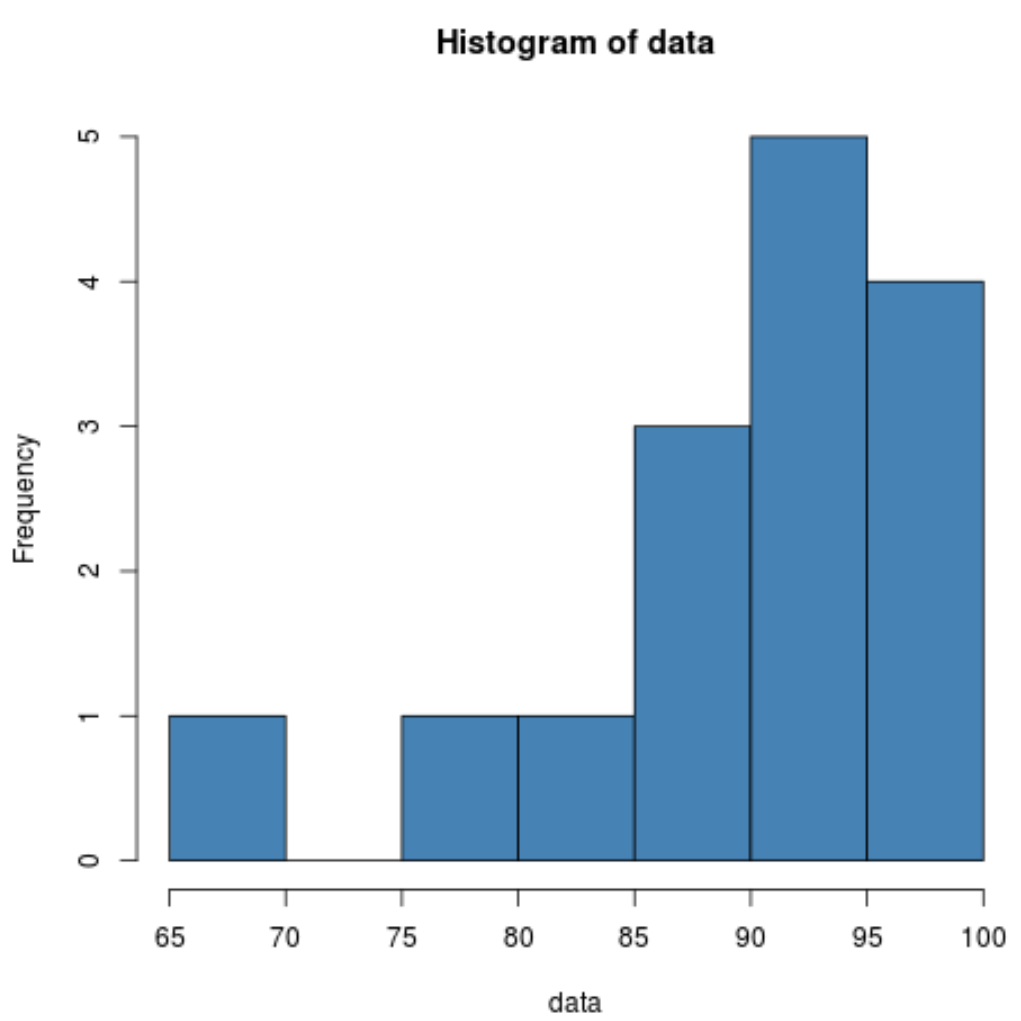
ฮิสโตแกรมแสดงให้เราเห็นว่าการกระจายตัวดูเหมือนจะเบ้ไปทางซ้าย นั่นคือค่าส่วนใหญ่จะกระจุกตัวอยู่ทางด้านขวาของการแจกแจง

ในการคำนวณความเบ้และความโด่งของชุดข้อมูลนี้ เราสามารถใช้ฟังก์ชัน ความเบ้() และ ความโด่ง () จากไลบรารี โมเมนต์ ใน R:

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

ความเบ้กลายเป็น -1.391777 และความโด่งกลายเป็น 4.177865 .

เนื่องจากความเบ้เป็นลบ จึงบ่งชี้ว่าการกระจายตัวยังคงเบ้ นี่เป็นการยืนยันสิ่งที่เราเห็นในฮิสโตแกรม

เนื่องจากความโด่งมีค่ามากกว่า 3 แสดงว่าการแจกแจงมีค่าในส่วนท้ายมากกว่าเมื่อเทียบกับการแจกแจงแบบปกติ

ไลบรารี Moments ยังมีฟังก์ชัน jarque.test() ซึ่งทำการทดสอบความพอดีที่จะกำหนดว่าข้อมูลตัวอย่างแสดงความเบ้และความโด่งที่สอดคล้องกับการแจกแจงแบบปกติหรือไม่ สมมติฐานว่างและทางเลือกของการทดสอบนี้มีดังนี้:

สมมติฐานว่าง : ชุดข้อมูลมีความเบ้และความโด่งที่สอดคล้องกับการแจกแจงแบบปกติ

สมมติฐานทางเลือก : ชุดข้อมูลมีความเบ้และโด่งที่ ไม่สอดคล้อง กับการแจกแจงแบบปกติ

รหัสต่อไปนี้แสดงวิธีดำเนินการทดสอบนี้:

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

ค่า p ของการทดสอบกลายเป็น 0.05756 เนื่องจากค่านี้ไม่น้อยกว่า α = 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ เราไม่มีหลักฐานเพียงพอที่จะบอกว่าชุดข้อมูลนี้มีความเบ้และความโด่งแตกต่างจากการแจกแจงแบบปกติ

คุณสามารถค้นหาเอกสาร Moments Library ฉบับเต็มได้ ที่นี่

โบนัส: เครื่องคำนวณความเบ้และความโด่ง

คุณยังสามารถคำนวณความเบ้สำหรับชุดข้อมูลที่กำหนดได้โดยใช้ เครื่องคำนวณความเบ้และความโด่งทางสถิติ ซึ่งจะคำนวณความเบ้และความโด่งสำหรับชุดข้อมูลที่กำหนดโดยอัตโนมัติ