ควินไทล์ส (สถิติ)

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

ในบทความนี้ เราจะอธิบายว่าควินไทล์คืออะไรและคำนวณอย่างไร คุณจะพบตัวอย่างการคำนวณควินไทล์ที่แก้ไขแล้วหลายตัวอย่าง นอกจากนี้ คุณจะสามารถคำนวณควินไทล์ของตัวอย่างทางสถิติใดๆ ด้วยเครื่องคิดเลขออนไลน์ได้

ควินไทล์คืออะไร?

ในสถิติ quintiles คือค่าสี่ค่าที่แบ่งชุดข้อมูลออกเป็นห้าส่วนเท่า ๆ กัน ดังนั้น ควินไทล์ที่หนึ่ง สอง สาม และสี่จึงคิดเป็น 20%, 40%, 60% และ 80% ของข้อมูลตัวอย่าง ตามลำดับ

นั่นคือค่าของควินไทล์ที่สามนั้นสูงกว่า 60% ของข้อมูลทั้งหมดที่รวบรวม แต่ต่ำกว่าข้อมูลที่เหลือ

สัญลักษณ์สำหรับควินไทล์คืออักษรตัวใหญ่ K โดยมีดัชนีควินไทล์ กล่าวคือ ควินไทล์ตัวแรกคือ K ₁ ควินไทล์ที่สองคือ K ₂ ควินไทล์ที่สามคือ K ₃ และควินไทล์ที่สี่คือ K ₄ แม้ว่าจะสามารถแสดงด้วยตัวอักษร Q ก็ได้ (ไม่แนะนำเนื่องจากจะทำให้สับสนกับควอไทล์)

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณควินไทล์สำหรับชุดข้อมูลใดก็ได้

ควินไทล์เป็นหน่วยวัดตำแหน่งที่ไม่เป็นศูนย์กลาง ร่วมกับควอร์ไทล์ เดซิล และเปอร์เซ็นไทล์ หากคุณสนใจมากขึ้น คุณสามารถตรวจสอบความหมายของควอนไทล์แต่ละประเภทได้ในเว็บไซต์ของเรา

ควรสังเกตว่า quintile อาจมีคำจำกัดความอื่น ในทางเศรษฐศาสตร์ กลุ่มควินไทล์แสดงถึงเปอร์เซ็นต์ของประชากรเรียงลำดับตามรายได้ หรืออีกนัยหนึ่ง คือ จัดอันดับประชากรตามระดับรายได้ ตัวอย่างเช่น กลุ่มแรกตรงกับกลุ่มคนที่ยากจนที่สุด 20% ในประชากร กลุ่มที่สองตรงกับกลุ่มประชากร 40% ที่มีรายได้ต่ำที่สุด เป็นต้น

วิธีการคำนวณควินไทล์

ใน การคำนวณตำแหน่งของควินไทล์ ของกลุ่มตัวอย่างหรือประชากรทางสถิติ คุณต้องคูณจำนวนควินไทล์ด้วยผลรวมของจำนวนข้อมูลทั้งหมดบวกหนึ่ง แล้วหารผลลัพธ์ด้วยห้า

ดังนั้น สูตรของควินไทล์ คือ:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

โปรดทราบ: ผลลัพธ์ของสูตรนี้บอกเราถึงตำแหน่งของควินไทล์ ไม่ใช่ค่าของมัน ดังนั้นควินไทล์จึงเป็นข้อมูลที่อยู่ในตำแหน่งที่ได้จากสูตร

อย่างไรก็ตาม บางครั้งผลลัพธ์ของสูตรนี้จะให้ค่าเป็นเลขทศนิยม ดังนั้น เราจึงต้องแยกความแตกต่างออกเป็น 2 กรณี ขึ้นอยู่กับว่าผลลัพธ์เป็นเลขทศนิยมหรือไม่:

หากผลลัพธ์ของสูตรเป็น ตัวเลขที่ไม่มีส่วนทศนิยม ค่า ควินไทล์คือข้อมูลที่อยู่ในตำแหน่งที่ระบุในสูตรด้านบน
หากผลลัพธ์ของสูตรเป็น ตัวเลขที่มีส่วนทศนิยม ค่าควินไทล์จะถูกคำนวณโดยใช้นิพจน์ต่อไปนี้:

$K=x_i+d\cdot (x_{i+1}-x_i)$

โดยที่ x _i และ x _i+1 คือตัวเลขของตำแหน่งระหว่างตำแหน่งที่มีตัวเลขที่ได้จากสูตรแรกอยู่ และ d คือส่วนทศนิยมของตัวเลขที่ได้จากสูตรแรก

หากคุณกลัวเมื่อเห็นขั้นตอนมากมายในการกำหนดควินไทล์ของชุดข้อมูล ไม่ต้องกังวล เพราะจริงๆ แล้วขั้นตอนนั้นค่อนข้างง่าย อ่านสองตัวอย่างต่อไปนี้แล้วคุณจะเข้าใจดีขึ้นอย่างแน่นอน

หมายเหตุ : ชุมชนทางสถิติยังไม่เห็นด้วยกับวิธีคำนวณควินไทล์มากนัก ดังนั้น คุณอาจพบหนังสือที่อธิบายแตกต่างออกไปเล็กน้อย

ตัวอย่างการคำนวณควินไทล์

ด้านล่างนี้เราจะให้แบบฝึกหัดสองข้อได้รับการแก้ไขทีละขั้นตอนเกี่ยวกับวิธีการรับควินไทล์จากชุดข้อมูล ดังนั้น คุณจึงเห็นได้สองกรณีที่เป็นไปได้ ในแบบฝึกหัดแรกผลลัพธ์ไม่เป็นทศนิยม และในแบบฝึกหัดที่สองผลลัพธ์ไม่เป็นทศนิยม

ตัวอย่างที่ 1

คำนวณควินไทล์ของชุดข้อมูลต่อไปนี้:

ดังที่คุณเห็นในคำอธิบายข้างต้น สูตรการหาตำแหน่งของควินไทล์คือ:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

พารามิเตอร์ n อ้างอิงถึงจำนวนข้อมูลทั้งหมด ซึ่งก็คือ 49 ดังนั้นเพื่อค้นหาตำแหน่งของควินไทล์แรก เราจำเป็นต้องแทนที่ n ด้วย 49 และ k ด้วย 1:

$\cfrac{1\cdot (49+1)}{5}=10 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_1=205$

จากสูตรเราได้หมายเลข 10 ซึ่งหมายความว่าควินไทล์อยู่ในตำแหน่งที่สิบของรายการเรียงลำดับซึ่งสอดคล้องกับข้อมูล 205

ในการคำนวณควินไทล์ที่สอง คุณต้องใช้สูตรเดียวกันแต่แทนที่ k ด้วย 2:

$\cfrac{2\cdot (49+1)}{5}=20 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_2=236$

ดังนั้นกลุ่มที่สองจึงอยู่ที่ตำแหน่งหมายเลข 20 ของรายการสั่งซื้อ ซึ่งก็คือค่า 236

อีกครั้ง เราทำซ้ำขั้นตอนเพื่อหาค่าควินไทล์ 3 แต่ตามหลักตรรกะแล้ว ตอนนี้เราแทนที่ k ด้วย 3:

$\cfrac{3\cdot (49+1)}{5}=30 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_3=266$

ดังนั้น ควินไทล์ที่สามคือข้อมูลที่อยู่ในตำแหน่ง 30 ซึ่งตรงกับ 266

สุดท้าย เราใช้สูตรอีกครั้งเพื่อคำนวณควินไทล์ที่สี่:

$\cfrac{4\cdot (49+1)}{5}=40 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_4=286$

ดังนั้นกลุ่มที่สี่จึงอยู่ในตำแหน่งที่ 40 ดังนั้นกลุ่มที่สี่จึงเป็น 286

ตัวอย่างที่ 2

คำนวณสี่ควินไทล์ของข้อมูลทางสถิติที่รวบรวมไว้ในตารางต่อไปนี้:

เช่นเดียวกับในตัวอย่างก่อนหน้านี้ เพื่อให้ได้ตำแหน่งของควินไทล์ คุณต้องใช้สูตรต่อไปนี้:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

ในกรณีนี้ ขนาดของกลุ่มตัวอย่างคือ 42 การสังเกต ดังนั้นเพื่อค้นหาตำแหน่งของควินไทล์แรก เราจำเป็นต้องแทนที่พารามิเตอร์ n ด้วย 42 และ k ด้วย 1:

$\cfrac{1\cdot (42+1)}{5}=8,6$

อย่างไรก็ตาม ครั้งนี้สูตรให้เลขทศนิยมแก่เรา ซึ่งต่างจากตัวอย่างแรก ดังนั้นเราจึงต้องใช้สูตรต่อไปนี้เพื่อคำนวณควินไทล์ที่แน่นอน:

$K=x_i+d\cdot (x_{i+1}-x_i)$

จำนวนที่ได้จากสูตรแรกคือ 8.6 ดังนั้นควินไทล์แรกจึงอยู่ระหว่างข้อมูลที่แปดและเก้าคือ 78 และ 79 ตามลำดับ ดังนั้น x _i คือ 78 x _i+1 คือ 79 และ d เป็นส่วนทศนิยมของตัวเลขที่ได้รับ เช่น 0.6

$K_1=78+0,6\cdot (79-78)=78,6$

ตอนนี้เราทำขั้นตอนเดิมอีกครั้งเพื่อค้นหาควินไทล์ที่สอง ก่อนอื่นเราคำนวณตำแหน่งของมัน:

$\cfrac{2\cdot (42+1)}{5}=17,2$

แต่จากสูตรเราได้เลขทศนิยมระหว่าง 17 ถึง 18 ดังนั้นควินไทล์ที่สองจะอยู่ระหว่างตำแหน่งที่สิบเจ็ดถึงสิบแปดซึ่งค่าจะสอดคล้องกับ 109 และ 112 ของรายการเรียงลำดับตามลำดับ ดังนั้นเราจึงใช้สูตรที่สองในกระบวนการเพื่อกำหนดค่าควินไทล์ที่แน่นอน:

$K_2=109+0,2\cdot (112-109)=109,6$

เราทำซ้ำวิธีการเพื่อให้ได้ควินไทล์ที่สามก่อนอื่นเราจะกำหนดตำแหน่งของมัน:

$\cfrac{3\cdot (42+1)}{5}=25,8$

จำนวนที่คำนวณได้ 25.8 หมายความว่าค่าควินไทล์จะอยู่ระหว่างตำแหน่งที่ยี่สิบห้าถึงยี่สิบหกซึ่งมีค่าเท่ากับ 134 และ 141 ดังนั้นการคำนวณค่าควินไทล์ที่แน่นอนจึงเป็น:

$K_3=134+0,8\cdot (141-134)=139,6$

สุดท้าย เราทำซ้ำขั้นตอนเดียวกันเป็นครั้งสุดท้ายเพื่อคำนวณควินไทล์ 4 ก่อนอื่นเราจะพบตำแหน่งของมัน:

$\cfrac{4\cdot (42+1)}{5}=34,4$

ดังนั้นค่าที่แน่นอนของควินไทล์ที่สี่จะอยู่ระหว่าง 34 ถึง 35 ซึ่งตำแหน่งตรงกับข้อมูล 172 และ 179 ดังนั้นการคำนวณควินไทล์ที่สี่จึงเป็นดังนี้:

$K_4=172+0,4\cdot (179-172)=174,8$

เครื่องคิดเลขควินไทล์

ป้อนข้อมูลทางสถิติที่กำหนดลงในเครื่องคิดเลขต่อไปนี้เพื่อคำนวณควินไทล์ ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

Quintiles ในข้อมูลที่จัดกลุ่ม

ใน การคำนวณควินไทล์เมื่อข้อมูลถูกจัดกลุ่มตามช่วงเวลา คุณต้องค้นหาช่วงเวลาหรือคลาสก่อนโดยใช้สูตรต่อไปนี้:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

ดังนั้นควินไทล์จึงอยู่ในช่วงที่ความถี่สัมบูรณ์มากกว่าจำนวนที่ได้รับจากนิพจน์ก่อนหน้าทันที

และเมื่อเรารู้ช่วงที่ควินไทล์อยู่ เราต้องใช้สูตรต่อไปนี้เพื่อค้นหาค่าที่แน่นอนของควินไทล์:

$K_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{5}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,4$

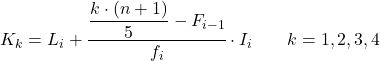
ทอง:

L _i คือขีดจำกัดล่างของช่วงเวลาที่ควินไทล์ตั้งอยู่
n คือจำนวนการสังเกตทั้งหมด
F _i-1 คือความถี่สัมบูรณ์สะสมของช่วงก่อนหน้า
f _i คือความถี่สัมบูรณ์ของช่วงเวลาที่ควินไทล์ตั้งอยู่
_ฉัน คือความกว้างของช่วงควินไทล์

เพื่อให้คุณสามารถดูวิธีการดำเนินการได้ ต่อไปนี้คือตัวอย่างการแก้ปัญหาของการคำนวณควินไทล์ของชุดข้อมูลต่อไปนี้ซึ่งจัดกลุ่มตามช่วงเวลา:

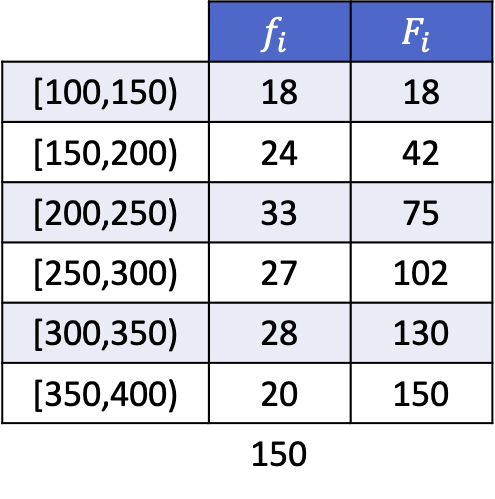
เนื่องจากข้อมูลถูกจัดกลุ่ม เราจึงต้องใช้วิธีต่อไปนี้ในการคำนวณควินไทล์ ขั้นแรกให้กำหนดช่วงที่ควินไทล์ตก จากนั้นจึงหาค่าที่แน่นอนของควินไทล์

ดังนั้น เพื่อหาช่วงเวลาที่ควินไทล์แรกอยู่ เราใช้สูตรต่อไปนี้:

$\cfrac{k\cdot (n+1)}{5}$

$\cfrac{1\cdot (150+1)}{5} =30,2 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [150,200)$

ควินไทล์แรกจะอยู่ในช่วงที่มีความถี่สัมบูรณ์สะสมมากกว่า 30.2 ทันที ในกรณีนี้คือช่วง [150,200) ซึ่งมีความถี่สัมบูรณ์สะสมเท่ากับ 42 และเมื่อเราทราบช่วงควินไทล์แล้ว เราจะใช้สูตรที่สองของ กระบวนการเพื่อกำหนดค่าที่แน่นอน:

$K_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{5}-F_{i-1}}{f_i}\cdot I_i$

$K_1=150+\cfrac{\displaystyle\frac{1\cdot (150+1)}{5}-18}{24}\cdot 50=175,42$

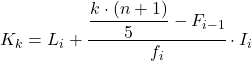
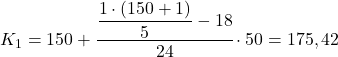
ตอนนี้เราทำซ้ำขั้นตอนเดียวกันเพื่อให้ได้ควินไทล์ที่สอง โดยก่อนอื่นให้คำนวณช่วงเวลาที่มันอยู่:

$\cfrac{2\cdot (150+1)}{5} =60,4 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [200,250)$

ความถี่สัมบูรณ์สะสมที่สูงกว่า 60.4 ทันทีคือ 75 ดังนั้นช่วงควินไทล์ที่สองคือ [200 250) ดังนั้นเราจึงแทนที่ค่าที่เกี่ยวข้องลงในสูตรที่สองเพื่อคำนวณค่าควินไทล์ที่แน่นอน:

$K_2=200+\cfrac{\displaystyle\frac{2\cdot (150+1)}{5}-42}{33}\cdot 50=227,88$

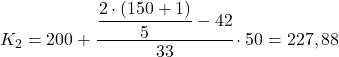
เราทำขั้นตอนเดียวกันเป็นครั้งที่สามเพื่อให้ได้ควินไทล์ 3 ขั้นแรกเราจะกำหนดช่วงเวลาที่ควินไทล์ตั้งอยู่:

$\cfrac{3\cdot (150+1)}{5} =90,6 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [250,300)$

ควินไทล์อยู่ในช่วง [250,300) เนื่องจากความถี่สัมบูรณ์สะสม (102) เป็นความถี่ที่สูงกว่า 90.6 ทันที การคำนวณค่าที่แน่นอนของควินไทล์ที่สามจึงเป็นดังนี้:

$K_3=250+\cfrac{\displaystyle\frac{3\cdot (150+1)}{5}-75}{27}\cdot 50=278,89$

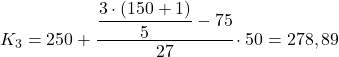
ในที่สุดเราก็จะพบกลุ่มที่สี่ และเช่นเคย เราจะหาช่วงเวลาของมันก่อน:

$\cfrac{4\cdot (150+1)}{5} =120,8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [300,350)$

ช่วงความถี่สัมบูรณ์ที่มากกว่า 120.8 ทันทีคือ [300.350) ซึ่งมีค่าเท่ากับ 130 ดังนั้นค่าที่แน่นอนของควินไทล์ที่สี่จะเป็น:

$K_4=300+\cfrac{\displaystyle\frac{4\cdot (150+1)}{5}-102}{28}\cdot 50=333,57$

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

ควินไทล์คืออะไร?

วิธีการคำนวณควินไทล์

ตัวอย่างการคำนวณควินไทล์

ตัวอย่างที่ 1

ตัวอย่างที่ 2

เครื่องคิดเลขควินไทล์

Quintiles ในข้อมูลที่จัดกลุ่ม

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น