T-score กับ z-score: ควรใช้เมื่อใด

คำสองคำที่มักสร้างความสับสนให้กับนักเรียนในหลักสูตรสถิติคือ t-score และ z-score

ทั้งสองใช้กันอย่างแพร่หลายเมื่อทำการ ทดสอบสมมติฐาน หรือสร้าง ช่วงความเชื่อมั่น แต่จะแตกต่างกันเล็กน้อย

นี่คือสูตรสำหรับแต่ละ:

คะแนน t = ( x – μ) / (s/√ n )

ทอง:

• x : หมายถึงตัวอย่าง
• μ : ค่าเฉลี่ยประชากร
• s : ตัวอย่างค่าเบี่ยงเบนมาตรฐาน
• n : ขนาดตัวอย่าง

คะแนน z = ( x – μ) / σ

ทอง:

• x : ค่าข้อมูลดิบ
• μ : ค่าเฉลี่ยประชากร
• σ : ส่วนเบี่ยงเบนมาตรฐานของประชากร

ผังงานนี้จะแสดงเมื่อคุณควรใช้แต่ละรายการ โดยพิจารณาจากข้อมูลของคุณ:

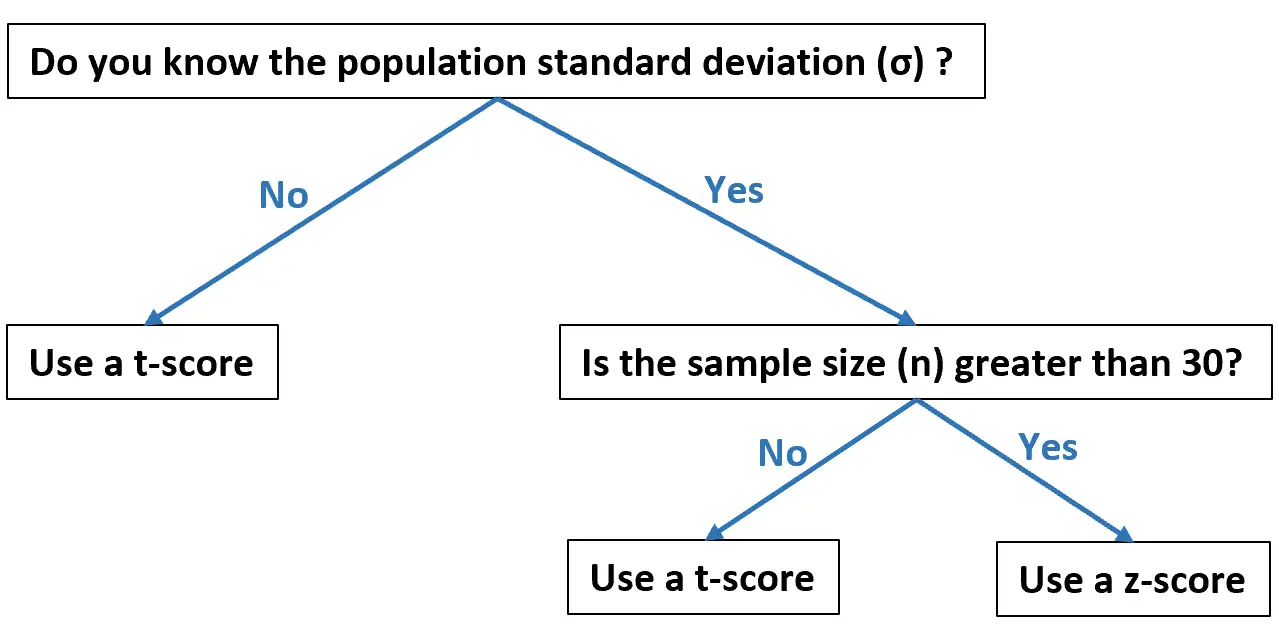
ตัวอย่างต่อไปนี้แสดงวิธีคำนวณคะแนน T และคะแนน Z ในทางปฏิบัติ

ตัวอย่างที่ 1: การคำนวณ T-Score

สมมติว่าร้านอาหารแห่งหนึ่งเตรียมแฮมเบอร์เกอร์โดยอ้างว่ามีน้ำหนักเฉลี่ย μ = 0.25 ปอนด์

สมมติว่าเราสุ่มตัวอย่างแฮมเบอร์เกอร์ n = 20 ชิ้น และพบว่าน้ำหนักเฉลี่ยของตัวอย่างคือ x = 0.22 ปอนด์ โดยมีค่าเบี่ยงเบนมาตรฐาน s = 0.05 ปอนด์ ทำการทดสอบสมมติฐานเพื่อตรวจสอบว่าน้ำหนักเฉลี่ยจริงของแฮมเบอร์เกอร์ทั้งหมดที่ผลิตโดยร้านอาหารแห่งนี้เท่ากับ 0.25 ปอนด์หรือไม่

สำหรับตัวอย่างนี้ เราจะใช้ คะแนน T เพื่อทำการทดสอบสมมติฐาน เนื่องจากไม่ตรงตามเงื่อนไขสองข้อต่อไปนี้

• ทราบค่าเบี่ยงเบนมาตรฐานของประชากร (σ) (σ ไม่ได้ระบุไว้ในตัวอย่างนี้)
• ขนาดตัวอย่างมากกว่า 30 (n=20 ในตัวอย่างนี้)

ดังนั้น เราจะคำนวณ t-score ดังนี้

• คะแนน t = ( x – μ) / (s/√ n )
• ทีสกอร์ = (0.22 – 0.25) / (0.05 / √ 20 )
• ทีสกอร์ = -2.68

จาก เครื่องคำนวณคะแนน T ค่า P ค่า p ที่สอดคล้องกับคะแนน t นี้คือ 0.01481

เนื่องจากค่า p นี้น้อยกว่า 0.05 เราจึงมีหลักฐานเพียงพอที่จะบอกว่าน้ำหนักเฉลี่ยของแฮมเบอร์เกอร์ที่ผลิตในร้านอาหารแห่งนี้ไม่เท่ากับ 0.25 ปอนด์

ตัวอย่างที่ 2: การคำนวณคะแนน Z

สมมติว่าบริษัทผลิตแบตเตอรี่ที่ทราบอายุการใช้งานตามการแจกแจงแบบปกติ โดยมีค่าเฉลี่ย μ = 20 ชั่วโมง และค่าเบี่ยงเบนมาตรฐาน σ = 5 ชั่วโมง

สมมติว่าเราสุ่มตัวอย่างแบตเตอรี่ n = 50 ก้อน และพบว่าค่าเฉลี่ยตัวอย่างคือ x = 21 ชั่วโมง ทำการทดสอบสมมติฐานเพื่อพิจารณาว่าอายุการใช้งานเฉลี่ยที่แท้จริงของแบตเตอรี่ทั้งหมดที่ผลิตโดยบริษัทนี้เท่ากับ 20 ชั่วโมงหรือไม่

สำหรับตัวอย่างนี้ เราจะใช้ คะแนน z เพื่อทำการทดสอบสมมติฐาน เนื่องจากตรงตามเงื่อนไขทั้งสองข้อต่อไปนี้:

• ทราบค่าเบี่ยงเบนมาตรฐานของประชากร (σ) (σ เท่ากับ 5 ในตัวอย่างนี้)
• ขนาดตัวอย่างมากกว่า 30 (n=50 ในตัวอย่างนี้)

ดังนั้น เราจะคำนวณคะแนน z ดังนี้

• คะแนน z = ( x – μ) / σ
• คะแนน z = (21 – 20) / 5
• คะแนน z = 0.2

จากเครื่องคำนวณคะแนน Z ค่า P ค่า p ที่สอดคล้องกับคะแนน z นี้คือ 0.84184

เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่มีหลักฐานเพียงพอที่จะกล่าวว่าอายุการใช้งานเฉลี่ยของแบตเตอรี่ทั้งหมดที่ผลิตโดยบริษัทนี้แตกต่างจาก 20 ชั่วโมง

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับคะแนน T และคะแนน Z:

การแจกแจงแบบปกติกับการแจกแจงแบบ t: อะไรคือความแตกต่าง?
วิธีอ่านตารางการแจกแจง
วิธีอ่านตาราง Z