คะแนน z ที่แก้ไขคืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)

ในสถิติ คะแนน z บอกเราว่าค่าหนึ่งๆ มาจาก ค่าเฉลี่ย เป็นจำนวนเท่าใด เราใช้สูตรต่อไปนี้เพื่อคำนวณคะแนน z:

คะแนน Z = (x _i – μ) / σ

ทอง:

• x _i : ค่าข้อมูลเดียว
• μ: ค่าเฉลี่ยของชุดข้อมูล
• σ: ค่าเบี่ยงเบนมาตรฐานของชุดข้อมูล

คะแนน Z มักใช้เพื่อตรวจจับค่าผิดปกติในชุดข้อมูล ตัวอย่างเช่น การสังเกตที่มีคะแนน z น้อยกว่า -3 หรือมากกว่า 3 มักถูกพิจารณาว่ามีค่าผิดปกติ

อย่างไรก็ตาม คะแนน z อาจได้รับผลกระทบจากค่าข้อมูลที่มีขนาดใหญ่หรือเล็กผิดปกติ นี่คือเหตุผลว่าทำไมวิธีที่มีประสิทธิภาพมากขึ้นในการตรวจจับค่าผิดปกติคือการใช้ คะแนน z ที่แก้ไขแล้ว ซึ่งคำนวณได้ดังนี้:

คะแนน z ที่แก้ไข = 0.6745 (x _i – x̃) / MAD

ทอง:

• x _i : ค่าข้อมูลเดียว
• x̃: ค่ามัธยฐานของชุดข้อมูล
• MAD: ค่ามัธยฐานส่วนเบี่ยงเบนสัมบูรณ์ของชุดข้อมูล

คะแนนมาตรฐานที่แก้ไขแล้วจะมีความเสถียรมากกว่า เนื่องจากใช้ค่ามัธยฐานในการคำนวณคะแนนมาตรฐาน ซึ่งตรงข้ามกับค่าเฉลี่ย ซึ่งทราบกันว่าได้รับอิทธิพลจากค่าผิดปกติ

Iglewicz และ Hoaglin แนะนำว่าค่าที่มีคะแนน z ที่แก้ไขน้อยกว่า -3.5 หรือมากกว่า 3.5 จะถูกระบุว่าเป็นค่าผิดปกติที่อาจเกิดขึ้น

ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีคำนวณคะแนน z ที่แก้ไขสำหรับชุดข้อมูลที่ระบุ

ขั้นตอนที่ 1: สร้างข้อมูล

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งมี 16 ค่า:

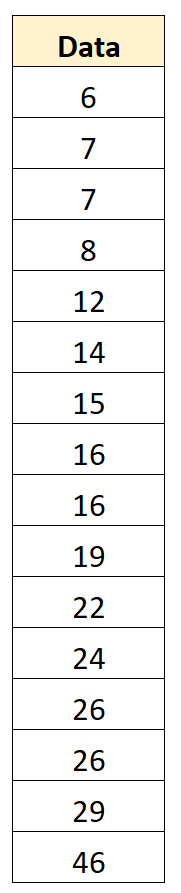
ขั้นตอนที่ 2: ค้นหาค่ามัธยฐาน

ต่อไปเราจะหาค่ามัธยฐาน นี่แสดงถึงจุดกึ่งกลางของชุดข้อมูล ซึ่งกลายเป็น 16

ขั้นตอนที่ 3: ค้นหาความแตกต่างสัมบูรณ์ระหว่างแต่ละค่ากับค่ามัธยฐาน

ต่อไป เราจะค้นหาความแตกต่างสัมบูรณ์ระหว่างค่าข้อมูลแต่ละค่ากับค่ามัธยฐาน ตัวอย่างเช่น ผลต่างสัมบูรณ์ระหว่างค่าข้อมูลแรกและค่ามัธยฐานจะถูกคำนวณดังนี้:

ผลต่างสัมบูรณ์ = |6 – 16| = 10

เราสามารถใช้สูตรเดียวกันในการคำนวณความแตกต่างสัมบูรณ์ระหว่างค่าข้อมูลแต่ละค่าและค่ามัธยฐาน:

ขั้นตอนที่ 4: ค้นหาค่าเบี่ยงเบนมัธยฐานสัมบูรณ์

ต่อไป เราจะหาค่าเบี่ยงเบนมัธยฐานสัมบูรณ์ นี่คือค่ามัธยฐานของคอลัมน์ที่สอง ซึ่งกลายเป็น 8

ขั้นตอนที่ 5: ค้นหาคะแนน Z ที่แก้ไขแล้วสำหรับค่าข้อมูลแต่ละค่า

สุดท้ายนี้ เราสามารถคำนวณคะแนน z ที่แก้ไขแล้วสำหรับค่าข้อมูลแต่ละค่าได้โดยใช้สูตรต่อไปนี้:

คะแนน z ที่แก้ไข = 0.6745 (x _i – x̃) / MAD

ตัวอย่างเช่น คะแนน z ที่แก้ไขแล้วสำหรับค่าข้อมูลแรกจะถูกคำนวณดังนี้:

คะแนน z ที่แก้ไขแล้ว = 0.6745*(6-16) / 8 = -0.843

เราสามารถทำซ้ำสูตรนี้สำหรับแต่ละค่าในชุดข้อมูล:

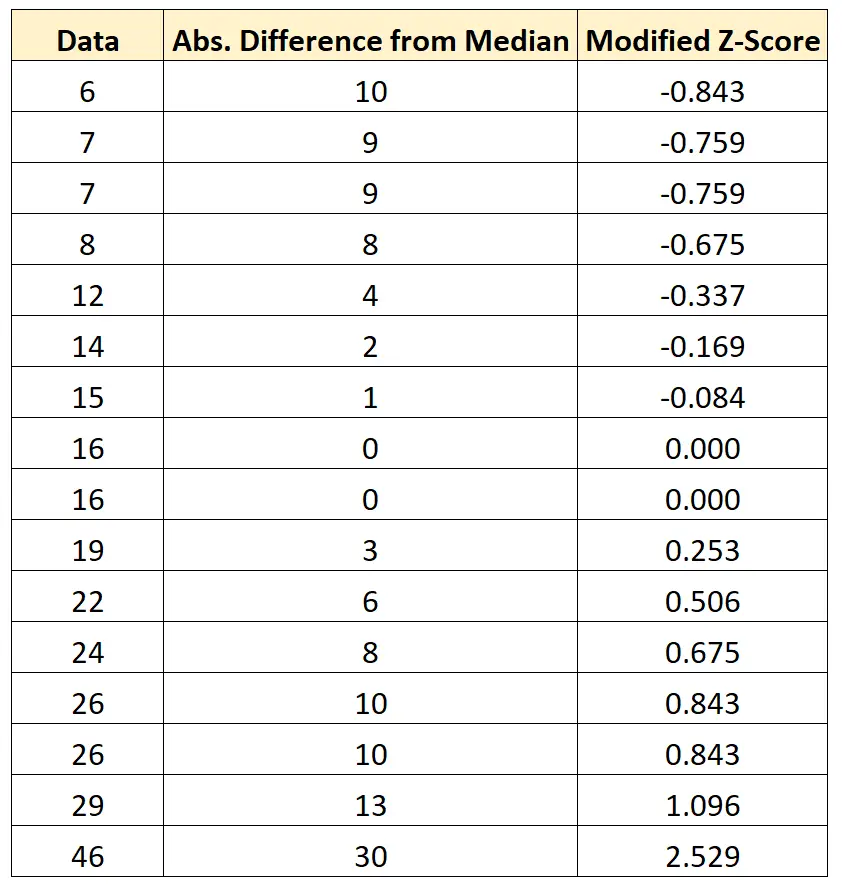
เราจะเห็นว่าไม่มีค่าใดในชุดข้อมูลที่มีคะแนน z ที่แก้ไขน้อยกว่า -3.5 หรือมากกว่า 3.5 ดังนั้นเราจึงไม่ได้ติดป้ายกำกับค่าใดๆ ในชุดข้อมูลนี้ว่าเป็นค่าผิดปกติที่อาจเกิดขึ้น

วิธีจัดการกับค่าผิดปกติ

หากมีค่าผิดปกติอยู่ในชุดข้อมูลของคุณ คุณจะมีหลายตัวเลือก:

• ตรวจสอบให้แน่ใจว่าค่าผิดปกติไม่ได้เป็นผลมาจากข้อผิดพลาดในการป้อนข้อมูล บางครั้งบุคคลเพียงแต่กรอกค่าข้อมูลที่ไม่ถูกต้องในขณะที่บันทึกข้อมูล หากมีค่าผิดปกติ ให้ตรวจสอบก่อนว่าค่าที่ป้อนถูกต้องและไม่ใช่ข้อผิดพลาด
• กำหนดค่าใหม่ให้กับค่าผิดปกติ หากค่าผิดปกติกลายเป็นผลลัพธ์ของข้อผิดพลาดในการป้อนข้อมูล คุณสามารถตัดสินใจกำหนดค่าใหม่ให้กับค่าดังกล่าวได้ เช่น ค่าเฉลี่ยหรือค่ามัธยฐาน ของชุดข้อมูล
• ลบค่าผิดปกติออก หากค่านั้นเป็นค่าผิดปกติจริงๆ คุณสามารถเลือกที่จะลบค่านั้นออกได้หากจะมีผลกระทบสำคัญต่อการวิเคราะห์โดยรวมของคุณ เพียงอย่าลืมพูดถึงในรายงานหรือการวิเคราะห์ขั้นสุดท้ายของคุณว่าคุณได้ลบค่าผิดปกติออก