วิธีการคำนวณคะแนน z ใน excel
ในสถิติ คะแนน z บอกเราว่าค่าหนึ่งๆ มาจาก ค่าเฉลี่ย เป็นจำนวนเท่าใด เราใช้สูตรต่อไปนี้เพื่อคำนวณคะแนน z:
z = (X – μ) / σ
ทอง:
- X คือค่าข้อมูลดิบค่าเดียว
- μ คือค่าเฉลี่ยของชุดข้อมูล
- σ คือค่าเบี่ยงเบนมาตรฐานของชุดข้อมูล
บทช่วยสอนนี้จะอธิบายวิธีคำนวณคะแนน z สำหรับค่าข้อมูลดิบใน Excel
วิธีการคำนวณคะแนน Z ใน Excel
สมมติว่าเรามีชุดข้อมูลต่อไปนี้ และต้องการค้นหาคะแนน z สำหรับค่าข้อมูลดิบแต่ละค่า:
เราสามารถทำตามขั้นตอนต่อไปนี้เพื่อทำสิ่งนี้
ขั้นตอนที่ 1: ค้นหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของชุดข้อมูล
ขั้นแรก เราต้องค้นหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของชุดข้อมูล สูตรต่อไปนี้แสดงวิธีการทำเช่นนี้:
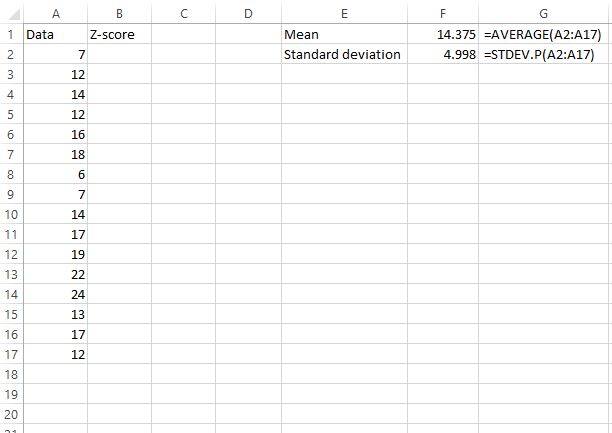
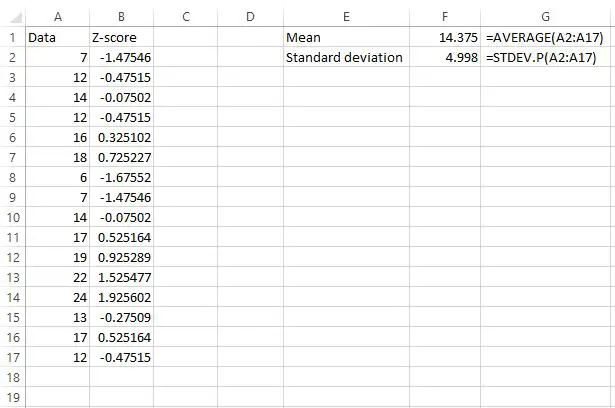
ค่าเฉลี่ยกลายเป็น 14.375 และส่วนเบี่ยงเบนมาตรฐานคือ 4.998
ขั้นตอนที่ 2: ค้นหาคะแนน z สำหรับค่าข้อมูลดิบค่าแรก
ต่อไป เราจะค้นหาคะแนน z สำหรับค่าข้อมูลดิบค่าแรกโดยใช้สูตร z = (X – μ) / σ
เซลล์ C2 แสดงสูตรที่เราใช้ในการคำนวณค่า z ในเซลล์ B2
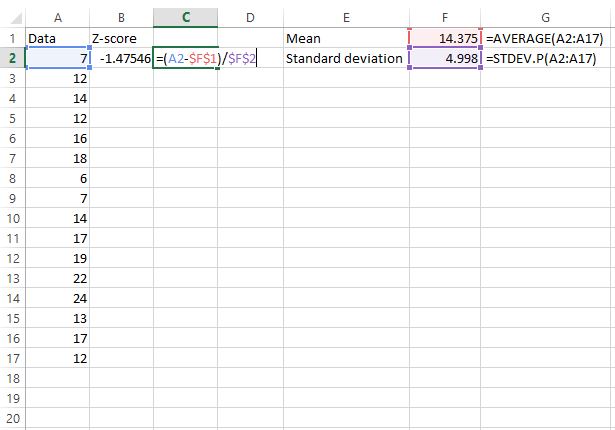
ขั้นตอนที่ 3: ค้นหาคะแนน z สำหรับค่าที่เหลือทั้งหมด
ตอนนี้เราพบคะแนน z สำหรับค่าแรกในชุดข้อมูลแล้ว เราก็สามารถคัดลอกสูตรที่เราใช้ในเซลล์ B2 ไปยังค่าข้อมูลที่เหลือได้ เราสามารถทำได้โดยการเน้นคอลัมน์คะแนน z ทั้งหมด โดยเริ่มจากคะแนน z แรกที่เราคำนวณไว้แล้ว:
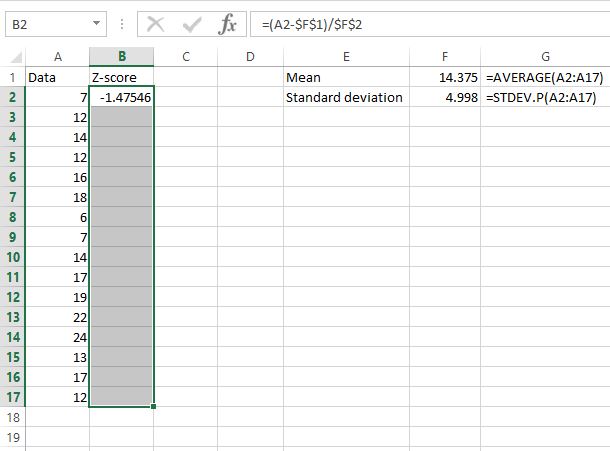
จากนั้นกด Ctrl+D เพื่อคัดลอกสูตรจากเซลล์แรกไปยังเซลล์ทั้งหมดที่อยู่ด้านล่าง
ตอนนี้เราพบคะแนน z สำหรับค่าข้อมูลดิบแต่ละค่าแล้ว
วิธีตีความคะแนน Z ใน Excel
โปรดจำไว้ว่า คะแนน z เพียงบอกเราว่าค่าหนึ่งๆ มาจากค่าเฉลี่ยเป็นจำนวนเท่าใด
คะแนน z อาจเป็นค่าบวก ลบ หรือศูนย์ก็ได้
คะแนน z เชิงบวกบ่งชี้ว่าค่าใดค่าหนึ่งสูงกว่าค่าเฉลี่ย คะแนน z ที่เป็นลบบ่งชี้ว่าค่าใดค่าหนึ่งนั้นต่ำกว่าค่าเฉลี่ย และคะแนน az ที่เป็นศูนย์บ่งชี้ว่าค่าใดค่าหนึ่งเท่ากับค่าเฉลี่ย
ในตัวอย่างของเรา เราพบว่าค่าเฉลี่ยคือ 14.375 และส่วนเบี่ยงเบนมาตรฐานคือ 4.998
ดังนั้นค่าแรกในชุดข้อมูลของเราคือ 7 ซึ่งมีคะแนน z (7-14.375) / 4.998 = -1.47546 ซึ่งหมายความว่าค่า “7” คือ -1.47545 ส่วนเบี่ยงเบนมาตรฐาน ที่ต่ำกว่า ค่าเฉลี่ย
ค่าถัดไปในข้อมูลของเรา 12 มีคะแนน z (12-14.375) / 4.998 = -0.47515 ซึ่งหมายความว่าค่า “12” คือ -0.47515 ส่วนเบี่ยงเบนมาตรฐาน ต่ำ กว่าค่าเฉลี่ย

ยิ่งค่าอยู่ห่างจากค่าเฉลี่ย ค่าสัมบูรณ์ของคะแนน z ก็จะยิ่งสูงขึ้นสำหรับค่านั้น
ตัวอย่างเช่น ค่า 7 อยู่ไกลจากค่าเฉลี่ย (14.375) มากกว่าค่า 12 ซึ่งอธิบายว่าทำไม 7 จึงมีคะแนน z ที่มีค่าสัมบูรณ์มากกว่า
แหล่งข้อมูลเพิ่มเติม
บทความต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับวิธีการทำงานกับคะแนน z ใน Excel:
วิธีค้นหาค่า P จากคะแนน Z ใน Excel
วิธีแปลงระหว่างคะแนน Z และเปอร์เซ็นไทล์ใน Excel