วิธีการคำนวณค่า p ใน excel (3 ตัวอย่าง)
ในสถิติ เราใช้ การทดสอบสมมติฐาน เพื่อพิจารณาว่าข้อความเกี่ยวกับ พารามิเตอร์ประชากร เป็นจริงหรือไม่
เมื่อเราทำการทดสอบสมมติฐาน เรามักจะได้รับสถิติการทดสอบ T-score
เมื่อเราพบสถิติการทดสอบ t-score แล้ว เราก็จะสามารถหาค่า p ที่เกี่ยวข้องได้
หากค่า p นี้น้อยกว่าค่าที่กำหนด (เช่น 0.10, 0.05, 0.01) เราจะปฏิเสธสมมติฐานว่างของการทดสอบ และสรุปว่าผลลัพธ์ของเรามีนัยสำคัญทางสถิติ
ตัวอย่างต่อไปนี้แสดงวิธีคำนวณค่า p สำหรับสถิติการทดสอบใน Excel ในสถานการณ์ที่แตกต่างกันสามสถานการณ์
ตัวอย่างที่ 1: คำนวณค่า P สำหรับการทดสอบแบบสองด้าน
สมมติว่านักพฤกษศาสตร์ต้องการทราบว่าความสูงเฉลี่ยของพืชบางชนิดเท่ากับ 15 นิ้วหรือไม่
ใน การสุ่มตัวอย่าง พืช 12 ต้น เธอพบว่าความสูงเฉลี่ยของตัวอย่างคือ 14.33 นิ้ว และค่าเบี่ยงเบนมาตรฐานของตัวอย่างคือ 1.37 นิ้ว
จะทำการทดสอบสมมติฐานโดยใช้สมมติฐานว่างและทางเลือกต่อไปนี้:
H 0 (สมมติฐานว่าง): μ= 15 นิ้ว
H A (สมมติฐานทางเลือก): μ ≠ 15 นิ้ว
สถิติการทดสอบคำนวณดังนี้:
- เสื้อ = ( X – µ) / (s/ √n )
- เสื้อ = (14.33-15) / (1.37/√ 12 )
- เสื้อ = -1.694
องศาอิสระที่เกี่ยวข้องกับสถิติการทดสอบนี้คือ n-1 = 12-1 = 11
หากต้องการค้นหาค่า p สำหรับสถิติการทดสอบนี้ เราจะใช้สูตรต่อไปนี้ใน Excel:
=T.DIST.2T(ABS(-1.694), 11)
ภาพหน้าจอต่อไปนี้แสดงวิธีใช้สูตรนี้ในทางปฏิบัติ
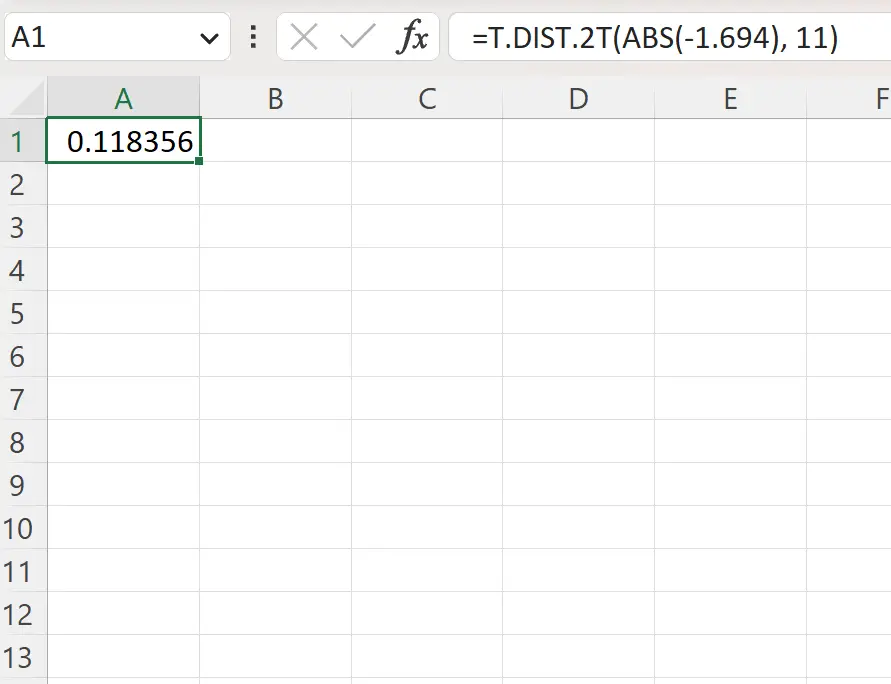
ค่า p แบบสองด้านคือ 0.1184
เนื่องจากค่านี้ ไม่น้อยกว่า 0.05 เราก็ปฏิเสธสมมติฐานว่างไม่ได้ เราไม่มีหลักฐานเพียงพอที่จะบอกว่าความสูงของพืชโดยเฉลี่ยแตกต่างจาก 15 นิ้ว
ตัวอย่างที่ 2: คำนวณค่า P สำหรับการทดสอบทางด้านซ้าย
สมมติว่าเราสมมติว่าน้ำหนักเฉลี่ยของอุปกรณ์บางอย่างที่ผลิตในโรงงานคือ 20 กรัม อย่างไรก็ตาม เจ้าหน้าที่ตรวจสอบประมาณน้ำหนักเฉลี่ยตามจริงให้น้อยกว่า 20 กรัม
เพื่อทดสอบสิ่งนี้ ระบบจะชั่งน้ำหนักตัวอย่างสุ่มอย่างง่ายจำนวน 20 วิดเจ็ต และรับข้อมูลต่อไปนี้:
- n = 20 วิดเจ็ต
- x = 19.8 กรัม
- ส = 3.1 กรัม
จากนั้นจะทำการทดสอบสมมติฐานโดยใช้สมมติฐานว่างและสมมติฐานทางเลือกต่อไปนี้:
H 0 (สมมติฐานว่าง): μ ≥ 20 กรัม
H A (สมมติฐานทางเลือก): μ < 20 กรัม
สถิติการทดสอบคำนวณดังนี้:
- เสื้อ = ( X – µ) / (s/ √n )
- เสื้อ = (19.8-20) / (3.1/√ 20 )
- เสื้อ = -.2885
องศาอิสระที่เกี่ยวข้องกับสถิติการทดสอบนี้คือ n-1 = 20-1 = 19
หากต้องการค้นหาค่า p สำหรับสถิติการทดสอบนี้ เราจะใช้สูตรต่อไปนี้ใน Excel:
=T.DIST(-.2885, 19, TRUE)
ภาพหน้าจอต่อไปนี้แสดงวิธีใช้สูตรนี้ในทางปฏิบัติ
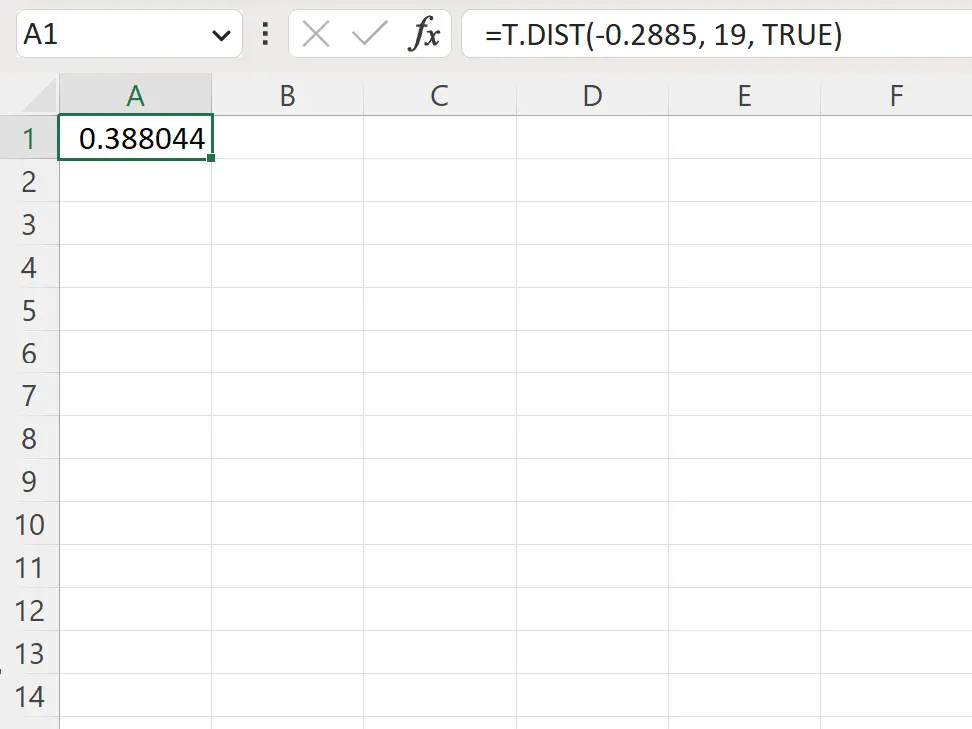
ค่า p ทางด้านซ้ายคือ 0.388044
เนื่องจากค่านี้ ไม่น้อยกว่า 0.05 ผู้ตรวจสอบไม่สามารถปฏิเสธสมมติฐานที่เป็นโมฆะได้ มีหลักฐานไม่เพียงพอที่จะบอกว่าน้ำหนักเฉลี่ยจริงของวิดเจ็ตที่ผลิตในโรงงานแห่งนี้คือน้อยกว่า 20 กรัม
หมายเหตุ : เราใช้อาร์กิวเมนต์ TRUE เพื่อระบุว่าควรใช้ฟังก์ชันการแจกแจงสะสมเมื่อคำนวณค่า p
ตัวอย่างที่ 3: คำนวณค่า P สำหรับการทดสอบทางด้านขวา
สมมติว่าความสูงเฉลี่ยของพืชบางชนิดคือ 10 นิ้ว อย่างไรก็ตาม นักพฤกษศาสตร์คนหนึ่งกล่าวว่าความสูงเฉลี่ยที่แท้จริงคือมากกว่า 10 นิ้ว
เพื่อทดสอบข้อกล่าวอ้างนี้ เธอวัดความสูงของ ตัวอย่างสุ่มอย่างง่าย จากพืช 15 ต้น และได้รับข้อมูลต่อไปนี้:
- n = 15 ต้น
- x = 11.4 นิ้ว
- ส = 2.5 นิ้ว
จากนั้นจะทำการทดสอบสมมติฐานโดยใช้สมมติฐานว่างและสมมติฐานทางเลือกต่อไปนี้:
H 0 (สมมติฐานว่าง): μ ≤ 10 นิ้ว
H A (สมมติฐานทางเลือก): μ > 10 นิ้ว
สถิติการทดสอบคำนวณดังนี้:
- เสื้อ = ( X – µ) / (s/ √n )
- เสื้อ = (11.4-10) / (2.5/√ 15 )
- เสื้อ = 2.1689
องศาอิสระที่เกี่ยวข้องกับสถิติการทดสอบนี้คือ n-1 = 15-1 = 14
หากต้องการค้นหาค่า p สำหรับสถิติการทดสอบนี้ เราจะใช้สูตรต่อไปนี้ใน Excel:
=T.DIST.RT(2.1689, 14)
ภาพหน้าจอต่อไปนี้แสดงวิธีใช้สูตรนี้ในทางปฏิบัติ
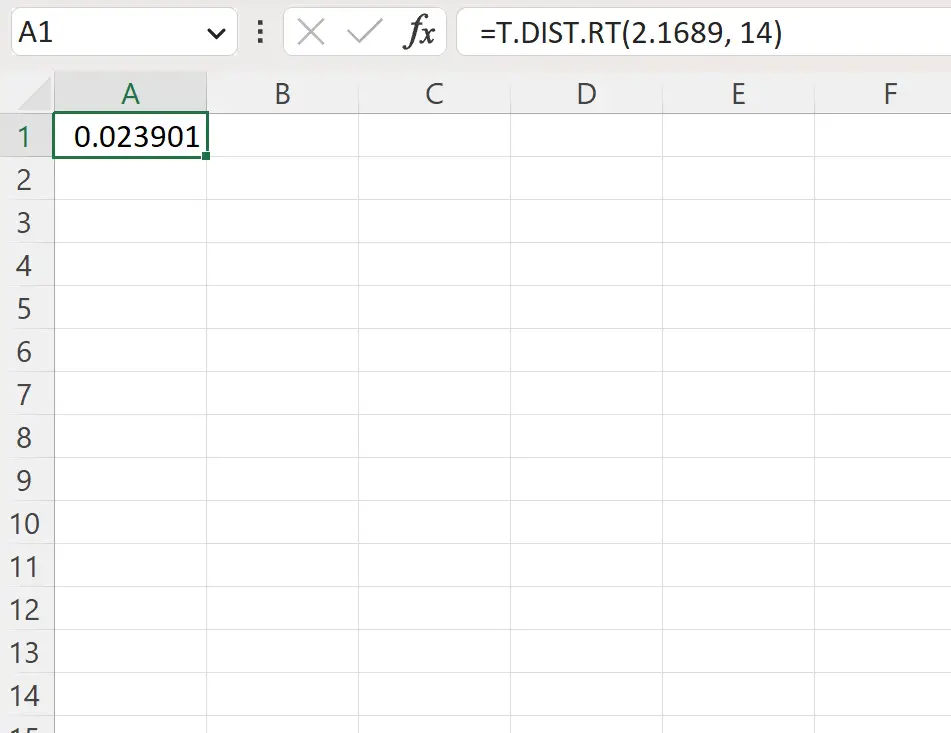
ค่า p ทางด้านขวาคือ 0.023901
ค่านี้น้อยกว่า 0.05 นักพฤกษศาสตร์สามารถปฏิเสธสมมติฐานว่างได้ เธอมีหลักฐานเพียงพอที่จะบอกว่าความสูงเฉลี่ยที่แท้จริงของพืชชนิดนี้คือมากกว่า 10 นิ้ว
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้อธิบายวิธีการทำงานทั่วไปอื่นๆ ใน Excel:
วิธีค้นหาค่า P จากคะแนน Z ใน Excel
วิธีค้นหาค่า P ของสถิติ F ใน Excel
วิธีค้นหาค่า P ของสถิติไคสแควร์ใน Excel