คุณภาพของความพอดี
บทความนี้จะอธิบายว่าความพอดีในสถิติเป็นอย่างไร ในทำนองเดียวกัน จะแสดงวิธีการวัดความดีของความพอดีของแบบจำลองการถดถอย และนอกจากนี้ คุณจะสามารถดูแบบฝึกหัดที่แก้ไขแล้วของความดีของความพอดีได้
ความดีของความพอดีคืออะไร?
ในสถิติ ความดีของความพอดี คือแบบจำลองการถดถอยเหมาะสมกับตัวอย่างข้อมูลได้ดีเพียงใด กล่าวอีกนัยหนึ่ง ความพอดีของแบบจำลองการถดถอยหมายถึงระดับของการมีเพศสัมพันธ์ระหว่างชุดการสังเกตและค่าที่ได้รับผ่านการถดถอย
ดังนั้น ยิ่งความพอดีของแบบจำลองการถดถอยดีเท่าไร ก็ยิ่งอธิบายข้อมูลที่กำลังศึกษาได้ดียิ่งขึ้นเท่านั้น ดังนั้นเราจึงต้องการให้โมเดลทางสถิติมีความเหมาะสมมากขึ้นเท่านั้น
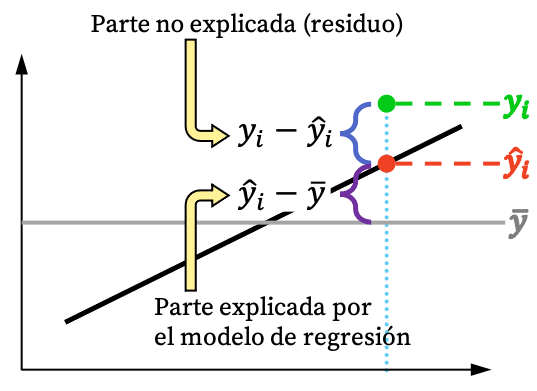
ดังที่คุณเห็นจากภาพด้านบน ค่าของการสังเกตมักจะไม่สามารถอธิบายได้ครบถ้วนด้วยแบบจำลองการถดถอย แต่ตามตรรกะแล้ว ยิ่งโมเดลการถดถอยสามารถอธิบายจากชุดข้อมูลได้มากเท่าใด โมเดลก็จะยิ่งพอดีมากขึ้นเท่านั้น กล่าวโดยสรุป เราสนใจแบบจำลองการถดถอยที่รัดกุมที่สุดเท่าที่จะเป็นไปได้
ความพอดีของแบบจำลองการถดถอย
ในการพิจารณาความพอดีของแบบจำลองการถดถอย โดยทั่วไปเราใช้ค่าสัมประสิทธิ์การกำหนด ซึ่งเป็นค่าสัมประสิทธิ์ทางสถิติที่ระบุเปอร์เซ็นต์ที่อธิบายโดยแบบจำลองการถดถอย ดังนั้น ยิ่งค่าสัมประสิทธิ์การกำหนดโมเดลสูงเท่าใด โมเดลก็จะยิ่งถูกปรับให้เข้ากับตัวอย่างข้อมูลได้ดีขึ้นเท่านั้น
![]()
อย่างไรก็ตาม ควรสังเกตว่ายิ่งแบบจำลองการถดถอยมีตัวแปรมากเท่าใด ค่าสัมประสิทธิ์การกำหนดก็จะยิ่งสูงขึ้นเท่านั้น ด้วยเหตุนี้ ค่าสัมประสิทธิ์การตัดสินใจที่ปรับแล้วจึงมักใช้เพื่อวัดความพอดีของแบบจำลองด้วย ค่าสัมประสิทธิ์การกำหนดที่ปรับแล้วคือการเปลี่ยนแปลงของค่าสัมประสิทธิ์ก่อนหน้า ซึ่งระบุเปอร์เซ็นต์ที่อธิบายโดยแบบจำลองการถดถอย ซึ่งจะลงโทษสำหรับตัวแปรอธิบายแต่ละตัวที่รวมอยู่ในแบบจำลอง
![]()
ดังนั้นจึงควรใช้ค่าสัมประสิทธิ์การตัดสินใจที่ปรับแล้วเพื่อเปรียบเทียบสองโมเดลกับตัวแปรที่แตกต่างกันจำนวนหนึ่ง เนื่องจากจะคำนึงถึงจำนวนตัวแปรที่รวมอยู่ในโมเดลด้วย
ท้ายที่สุด ควรสังเกตว่าการทดสอบไคสแควร์สามารถใช้เพื่อวัดความพอดีของแบบจำลองการถดถอยได้ แม้ว่าปกติจะใช้ค่าของสัมประสิทธิ์สองตัวก่อนหน้าก็ตาม
ตัวอย่างที่เป็นรูปธรรมของความพอดีที่ดี
ในที่สุด เราจะเห็นแบบฝึกหัดที่ได้รับการแก้ไขในด้านคุณภาพของการปรับตัวเพื่อเสร็จสิ้นการดูดซึมแนวคิดทางสถิตินี้
- ด้วยชุดข้อมูลเดียวกัน จะมีการดำเนินการแบบจำลองการถดถอยเชิงเส้นที่แตกต่างกันสองแบบ ซึ่งคุณสามารถดูผลลัพธ์ได้ในตารางต่อไปนี้ ใช้รุ่นไหนดีที่สุด?
| โมเดลการถดถอย 1 | โมเดลการถดถอย 2 | |
|---|---|---|
| ค่าสัมประสิทธิ์การตัดสินใจ | 57% | 64% |
| ปรับค่าสัมประสิทธิ์การตัดสินใจแล้ว | 49% | 43% |
| จำนวนตัวแปรอธิบาย | 3 | 7 |
ในกรณีนี้ เราถือว่าแบบจำลองทั้งสองเป็นไปตามสมมติฐานก่อนหน้านี้ของแบบจำลองการถดถอยเชิงเส้น ดังนั้น เราเพียงต้องวิเคราะห์ความดีของความพอดีของแบบจำลองเท่านั้น
โมเดลการถดถอย 2 มีค่าสัมประสิทธิ์การตัดสินใจที่สูงกว่าแบบจำลองการถดถอย 1 ดังนั้นจึงดูเหมือนว่าเป็นแบบจำลองการถดถอยที่ดีกว่า เนื่องจากสามารถอธิบายตัวอย่างข้อมูลได้ดีขึ้น
อย่างไรก็ตาม โมเดลการถดถอย 2 มีตัวแปรอิสระ 7 ตัวในแบบจำลอง ในขณะที่แบบจำลองการถดถอย 1 มีเพียง 3 ตัว ดังนั้นโมเดล 2 จะซับซ้อนกว่ามากและตีความยากกว่าแบบจำลองแรกมาก
นอกจากนี้ หากเราดูค่าสัมประสิทธิ์การกำหนดที่ปรับแล้ว ซึ่งคำนึงถึงจำนวนตัวแปรในแบบจำลอง โมเดลการถดถอย 1 จะมีค่าสัมประสิทธิ์การกำหนดที่ปรับแล้วสูงกว่าแบบจำลองการถดถอย 2
โดยสรุป แม้ว่าจะดีกว่าถ้าใช้แบบจำลองการถดถอย 1 เนื่องจากค่าสัมประสิทธิ์การกำหนดที่ปรับแล้วนั้นสูงกว่าแบบจำลองการถดถอย 2 แบบจำลองการถดถอย 2 มีค่าสัมประสิทธิ์การกำหนดที่ยังไม่ได้ปรับปรุงที่สูงกว่า เป็นเพราะพวกเขารวมตัวแปรอื่น ๆ อีกมากมายในการถดถอย แบบจำลอง 1. แบบจำลองซึ่งเพิ่มค่าสัมประสิทธิ์ดังกล่าวแต่ทำให้การตีความแบบจำลองยากขึ้น และทำให้การทำนายค่าใหม่แย่ลงอย่างแน่นอน
หากต้องการเปรียบเทียบแบบจำลองที่มีจำนวนตัวแปรต่างกัน วิธีที่ดีที่สุดคือใช้ค่าสัมประสิทธิ์การกำหนดที่ปรับแล้ว เนื่องจากค่าสัมประสิทธิ์จะถูกลงโทษสำหรับตัวแปรแต่ละตัวที่เพิ่มเข้าไปในแบบจำลอง ดังที่คุณเห็นในตัวอย่างนี้ ตามค่าสัมประสิทธิ์การตัดสินใจที่ยังไม่ได้ปรับปรุง โมเดลการถดถอย 2 จะดีกว่า อย่างไรก็ตาม ด้วยค่าสัมประสิทธิ์การตัดสินใจที่ปรับแล้ว เราจะรู้ได้ว่าแบบจำลองการถดถอย 1 ดีกว่าจริงๆ