5 ตัวอย่างค่าผิดปกติในชีวิตจริง

ค่า ผิดปกติ คือจุดข้อมูลที่อยู่ห่างจากค่าอื่นๆ ในชุดข้อมูลอย่างผิดปกติ

เรามักจะกำหนดจุดข้อมูลเป็นค่าผิดปกติหากเป็น 1.5 เท่าของช่วงระหว่างควอร์ไทล์เหนือควอไทล์ที่ 3 หรือ 1.5 เท่าของช่วงระหว่างควอไทล์ที่ต่ำกว่าควอไทล์แรกของชุดข้อมูล

หมายเหตุ : ช่วงระหว่างควอไทล์คือความแตกต่างระหว่างควอไทล์ที่สาม (เปอร์เซ็นไทล์ที่ 75) และควอร์ไทล์ที่หนึ่ง (เปอร์เซ็นไทล์ที่ 25) ของชุดข้อมูล

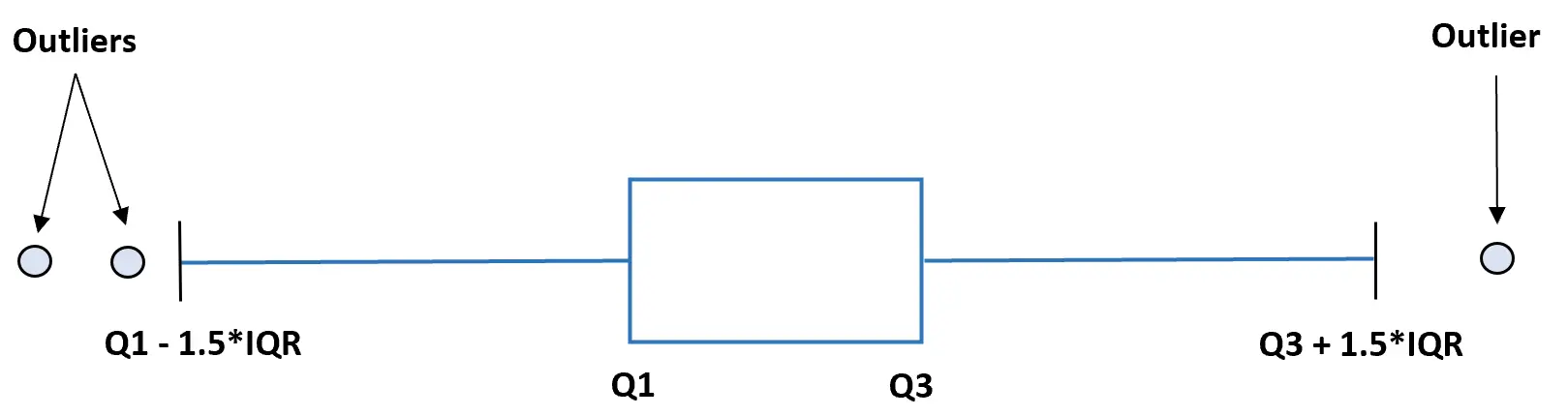
สถานการณ์ต่อไปนี้แสดงตัวอย่างค่าผิดปกติในสถานการณ์จริง

ตัวอย่างที่ 1: ค่าผิดปกติของรายได้

สถานการณ์ที่เป็นรูปธรรมซึ่งค่าผิดปกติมักปรากฏขึ้นคือการกระจายรายได้

ตัวอย่างเช่น เปอร์เซ็นไทล์ที่ 25 (Q1) ของรายได้ต่อปีในบางประเทศอาจเป็น 15,000 ดอลลาร์สหรัฐฯ ต่อปี และเปอร์เซ็นไทล์ที่ 75 (ไตรมาส 3) อาจเป็น 120,000 ดอลลาร์ต่อปี

ช่วงระหว่างควอไทล์ (IQR) จะถูกคำนวณดังนี้: 120,000 ดอลลาร์ – 15,000 ดอลลาร์ = 105,000 ดอลลาร์

ซึ่งหมายความว่าใครก็ตามที่มีรายได้เกินขีดจำกัดต่อไปนี้จะถือเป็นค่าผิดปกติ:

• ขีดจำกัดล่าง : ไตรมาสที่ 1 – 1.5*IQR = $15,000 – 1.5*$105,000 = -$142,500
• ขีดจำกัดบน : ไตรมาส 3 + 1.5*IQR = 120,000 ดอลลาร์ + 1.5*105,000 ดอลลาร์ = 277,500 ดอลลาร์

คนอย่าง Elon Musk ซึ่งมีมูลค่าสุทธิเป็นล้านล้านดอลลาร์ จะได้รับการพิจารณาว่าเป็นรายได้ที่สูงกว่าปกติในแง่ของรายได้ต่อปี

หมายเหตุ : ค่าของค่าผิดปกติที่เกินขีดจำกัดล่างอาจไม่มีความหมายเสมอไป เช่น ไม่สามารถหารายได้ต่อปีติดลบได้

ตัวอย่างที่ 2: ค่าผิดปกติของภาวะหยุดหายใจขณะหลับ

อีกสถานการณ์ในโลกแห่งความเป็นจริงที่ค่าผิดปกติมักปรากฏอยู่ในภาวะหยุดหายใจขณะหลับ

ตัวอย่างเช่น เปอร์เซ็นไทล์ที่ 25 (Q1) ของระยะเวลาที่บุคคลสามารถกลั้นหายใจได้คือประมาณ 15 วินาที ในขณะที่เปอร์เซ็นไทล์ที่ 75 (Q3) คือประมาณ 75 วินาที

ช่วงระหว่างควอไทล์ (IQR) จะถูกคำนวณดังนี้ 75 – 15 = 60

ซึ่งหมายความว่าใครก็ตามที่สามารถกลั้นหายใจได้นอกเหนือขีดจำกัดต่อไปนี้จะถือว่าผิดปกติ:

• ขีดจำกัดล่าง : Q1 – 1.5*IQR = 15 – 1.5*60 = -75 วินาที
• ขีดจำกัดบน : Q3 + 1.5*IQR = 75 + 1.5*60 = 165 วินาที

นักดำน้ำแบบฟรีไดฟ์ ทุกคนที่สามารถกลั้นหายใจได้ตั้งแต่ 10 นาทีขึ้นไปจะถือว่าผิดปกติเพราะสามารถกลั้นหายใจได้นานกว่า 165 วินาทีมาก

ตัวอย่างที่ 3: ค่าผิดปกติของขนาดสัตว์

สถานการณ์ในโลกแห่งความเป็นจริงอีกสถานการณ์หนึ่งที่ค่าผิดปกติมักปรากฏขึ้นคือขนาดของสัตว์

ตัวอย่างเช่น เปอร์เซ็นไทล์ที่ 25 (Q1) ของความสูงของม้าจะอยู่ที่ประมาณ 5 ฟุต และเปอร์เซ็นไทล์ที่ 75 (Q3) อยู่ที่ประมาณ 5.5 ฟุต

ช่วงระหว่างควอไทล์ (IQR) จะคำนวณได้ดังนี้ 5.5 – 5 = 0.5 ฟุต

ซึ่งหมายความว่าม้าตัวใดก็ตามที่มีขนาดเกินขีดจำกัดต่อไปนี้จะถือเป็นค่าผิดปกติ:

• ขีดจำกัดล่าง : Q1 – 1.5*IQR = 5 – 1.5*0.5 = 4.25 ฟุต
• ขีดจำกัดบน : Q3 + 1.5*IQR = 5 + 1.5*0.5 = 5.75 ฟุต

จากข้อมูลของ Guinness World Records สถิติของม้าที่สูงที่สุดตลอดกาลอยู่ที่เพียง 7 ฟุตเท่านั้น เนื่องจากความสูงนี้สูงกว่าขีดจำกัดบนที่ 5.75 ฟุต ม้าตัวนี้จึงถือว่าผิดปกติอย่างชัดเจน

ตัวอย่างที่ 4: ค่าผิดปกติในการขายตั๋วภาพยนตร์

สถานการณ์ในโลกแห่งความเป็นจริงอีกสถานการณ์หนึ่งที่ความผิดปกติมักปรากฏอยู่ในการขายตั๋วภาพยนตร์

ตัวอย่างเช่น เปอร์เซ็นไทล์ที่ 25 (Q1) ของยอดขายตั๋วภาพยนตร์รวมอยู่ที่ประมาณ 2 ล้านดอลลาร์ และเปอร์เซ็นไทล์ที่ 75 (Q3) อยู่ที่ประมาณ 15 ล้านดอลลาร์

ช่วงระหว่างควอไทล์ (IQR) จะคำนวณดังนี้: 15 ล้านเหรียญสหรัฐ – 2 ล้านเหรียญสหรัฐ = 13 ล้านเหรียญสหรัฐ

ซึ่งหมายความว่าภาพยนตร์ใดๆ ที่มียอดขายรวมเกินขีดจำกัดต่อไปนี้จะถือเป็นค่าผิดปกติ:

• ขีดจำกัดล่าง : T1 – 1.5*IQR = 2 ล้านดอลลาร์ – 1.5*13 ล้านดอลลาร์ = -17.5 ล้านดอลลาร์
• ขีดจำกัดบน : T3 + 1.5*IQR = 15 ล้านดอลลาร์ + 1.5*13 ล้านดอลลาร์ = 34.5 ล้านดอลลาร์

ภาพยนตร์ Star Wars ส่วนใหญ่ทำรายได้ได้มากกว่า 34.5 ล้านเหรียญสหรัฐ ซึ่งทำให้มียอดขายตั๋วที่ผิดปกติ

ตัวอย่างที่ 5: ค่าผิดปกติของคะแนนต่อเกม

อีกด้านในโลกแห่งความเป็นจริงที่ความผิดปกติมักปรากฏคือกีฬาอาชีพ

ตัวอย่างเช่น เปอร์เซ็นไทล์ที่ 25 (Q1) ของคะแนนที่ผู้เล่น NBA ทำได้คือประมาณ 5 แต้มต่อเกม และเปอร์เซ็นไทล์ที่ 75 (Q3) คือประมาณ 15 แต้มต่อเกม

ช่วงระหว่างควอไทล์ (IQR) จะคำนวณได้ดังนี้ 15 – 5 = 10 จุด

ซึ่งหมายความว่าผู้เล่นคนใดก็ตามที่มีค่าเฉลี่ยอยู่นอกขีดจำกัดต่อไปนี้จะถือว่าเป็นค่าผิดปกติ:

• ขีดจำกัดล่าง : Q1 – 1.5*IQR = 5 – 1.5*10 = -10 จุด
• ขีดจำกัดบน : Q3 + 1.5*IQR = 15 + 1.5*10 = 30 จุด

ใน หลายฤดูกาลของ NBA ผู้เล่นที่ทำคะแนนสูงสุดมักจะทำคะแนนได้มากกว่า 30 แต้มต่อเกม ทำให้เขากลายเป็นผู้เล่นที่แตกต่างจากปกติ

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีค้นหาค่าผิดปกติในชุดข้อมูลโดยใช้ซอฟต์แวร์ทางสถิติต่างๆ:

วิธีค้นหาค่าผิดปกติใน Excel
วิธีค้นหาค่าผิดปกติใน R
วิธีค้นหาค่าผิดปกติใน Python
วิธีค้นหาค่าผิดปกติใน SPSS