วิธีการคำนวณค่าสัมประสิทธิ์ phi ในหน่วย r
ค่าสัมประสิทธิ์พี (บางครั้งเรียกว่า ค่าสัมประสิทธิ์ฉุกเฉินกำลังสองเฉลี่ย ) คือการวัดความสัมพันธ์ระหว่างตัวแปรไบนารี่สองตัว
สำหรับตาราง 2×2 ที่กำหนดให้กับตัวแปรสุ่มสองตัว x และ y :

ค่าสัมประสิทธิ์พีสามารถคำนวณได้ดังนี้:
Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)
ตัวอย่าง: การคำนวณค่าสัมประสิทธิ์ Phi ในหน่วย R
สมมติว่าเราต้องการทราบว่าเพศสัมพันธ์กับการเลือกพรรคการเมืองหรือไม่ ดังนั้นเราจึง สุ่มตัวอย่างง่ายๆ จากผู้มีสิทธิเลือกตั้ง 25 คน และถามพวกเขาเกี่ยวกับการเลือกพรรคการเมืองที่พวกเขาชอบ
ตารางต่อไปนี้แสดงผลการสำรวจ:
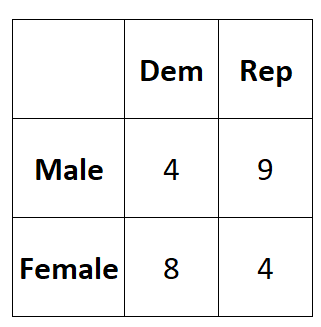
เราสามารถใช้โค้ดต่อไปนี้เพื่อป้อนข้อมูลนี้ลงในเมทริกซ์ 2×2 ใน R:
#create 2x2 table data = matrix(c(4, 8, 9, 4), nrow = 2 ) #view dataset data [,1] [,2] [1,] 4 9 [2,] 8 4
จากนั้นเราสามารถใช้ฟังก์ชัน phi() จากแพ็คเกจ Psych เพื่อคำนวณค่าสัมประสิทธิ์ Phi ระหว่างตัวแปรทั้งสอง:
#load psych package library (psych) #calculate Phi Coefficient phi(data) [1] -0.36
ค่าสัมประสิทธิ์พีกลายเป็น -0.36 .
โปรดทราบว่าฟังก์ชัน phi จะปัดเศษเป็น 2 หลักตามค่าเริ่มต้น แต่คุณสามารถระบุฟังก์ชันให้ปัดเศษเป็นตัวเลขได้มากเท่าที่คุณต้องการ:
#calculate Phi Coefficient and round to 6 digits phi(data, digits = 6 ) [1] -0.358974
วิธีการตีความค่าสัมประสิทธิ์พี
เช่นเดียวกับค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน ค่าสัมประสิทธิ์ Phi รับค่าระหว่าง -1 ถึง 1 โดยที่:
- -1 แสดงถึงความสัมพันธ์เชิงลบอย่างสมบูรณ์ระหว่างตัวแปรทั้งสอง
- 0 หมายถึงไม่มีการเชื่อมโยงระหว่างตัวแปรทั้งสอง
- 1 แสดงถึงความสัมพันธ์เชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรทั้งสอง
โดยทั่วไป ยิ่งค่าสัมประสิทธิ์ Phi จากศูนย์มากเท่าไร ความสัมพันธ์ระหว่างตัวแปรทั้งสองก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น
กล่าวอีกนัยหนึ่ง ยิ่งค่าสัมประสิทธิ์ Phi อยู่ห่างจากศูนย์มากเท่าใด ยิ่งมีหลักฐานที่แสดงถึงรูปแบบที่เป็นระบบบางประเภทระหว่างตัวแปรทั้งสองมากขึ้นเท่านั้น
แหล่งข้อมูลเพิ่มเติม
ความรู้เบื้องต้นเกี่ยวกับค่าสัมประสิทธิ์พี
เครื่องคำนวณค่าสัมประสิทธิ์พี