วิธีการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ภายในคลาสใน excel

ค่าสัมประสิทธิ์สหสัมพันธ์ภายในคลาส (ICC) ใช้เพื่อพิจารณาว่ารายการ (หรือหัวข้อ) สามารถจัดอันดับได้อย่างน่าเชื่อถือโดยผู้ประเมินที่แตกต่างกันหรือไม่

ค่าของ ICC สามารถอยู่ในช่วงตั้งแต่ 0 ถึง 1 โดย 0 หมายถึงไม่มี ความน่าเชื่อถือ ในหมู่ผู้ประเมิน และ 1 หมายถึงความน่าเชื่อถือที่สมบูรณ์แบบ

บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีคำนวณ ICC ใน Excel

ขั้นตอนที่ 1: สร้างข้อมูล

สมมติว่าผู้พิพากษาสี่คนถูกขอให้ประเมินคุณภาพของการสอบเข้าวิทยาลัยที่แตกต่างกัน 10 รายการ ผลลัพธ์แสดงไว้ด้านล่าง:

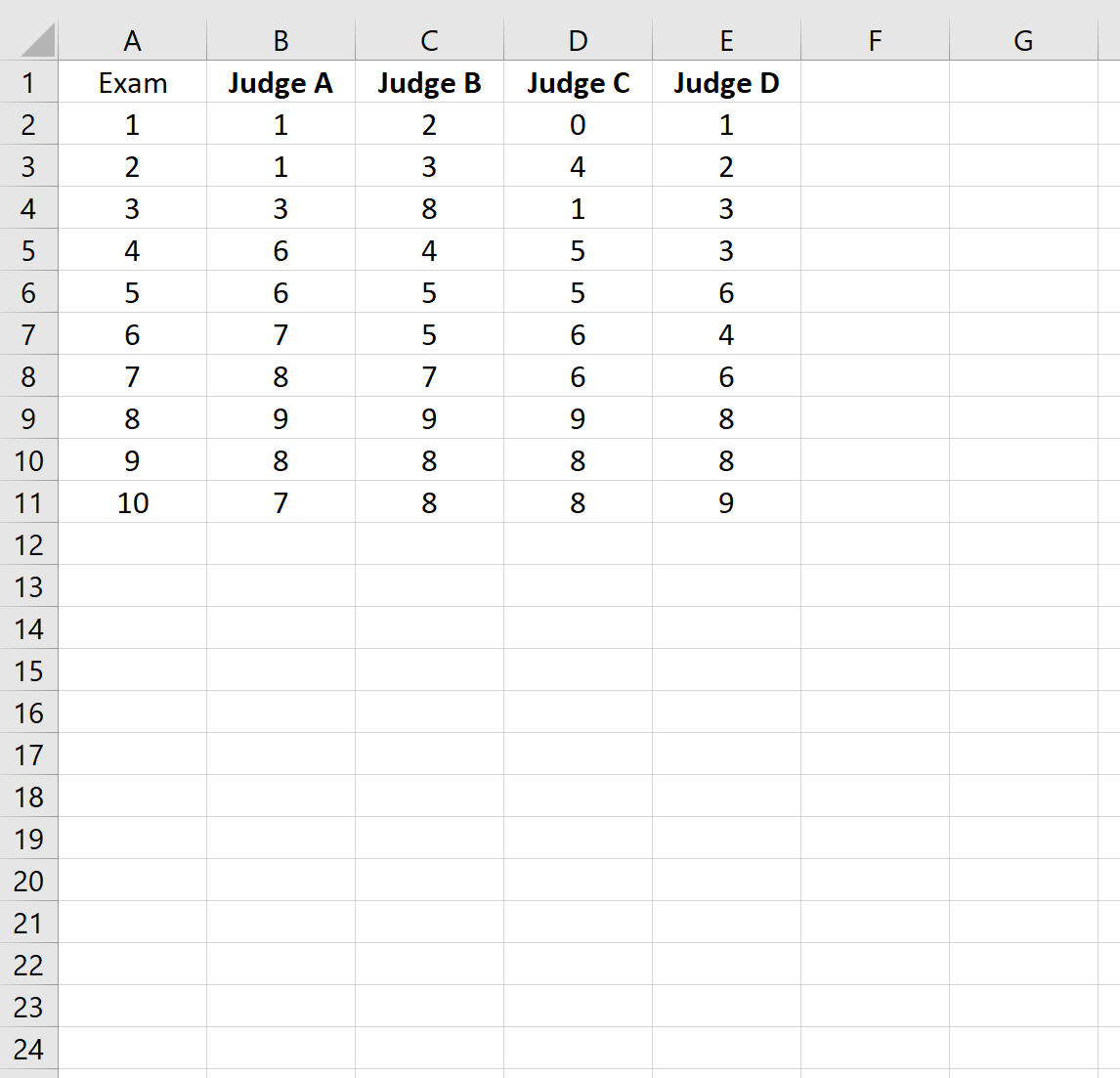
ขั้นตอนที่ 2: ปรับ ANOVA ให้พอดี

ในการคำนวณ ICC สำหรับการให้คะแนนเหล่านี้ เราต้องปรับ Anova: Two-Factor Without Replication ก่อน

เมื่อต้องการทำเช่นนี้ ให้เน้นเซลล์ A1:E11 ดังนี้:

เมื่อต้องการทำเช่นนี้ ให้คลิกแท็บ ข้อมูล ใน Ribbon ด้านบน จากนั้นคลิกตัวเลือก การวิเคราะห์ข้อมูล ใต้กลุ่ม การวิเคราะห์ :

หากไม่มีตัวเลือกนี้ คุณต้อง โหลด Analysis ToolPak ก่อน

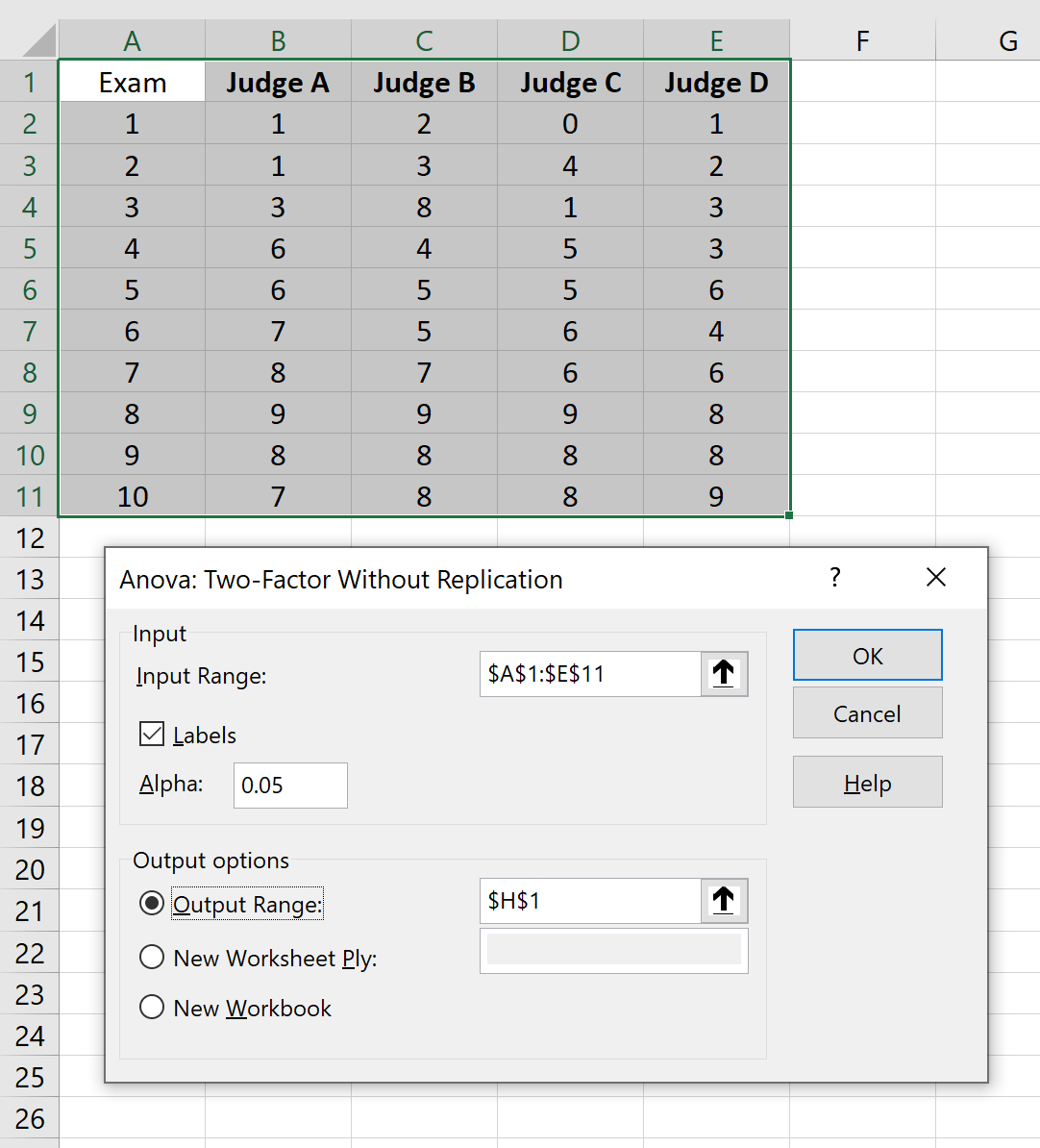
ในเมนูแบบเลื่อนลงที่ปรากฏขึ้น คลิก Anova: Two-Factor Without Replication จากนั้นคลิก ตกลง ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้ระบุข้อมูลต่อไปนี้ จากนั้นคลิก ตกลง :

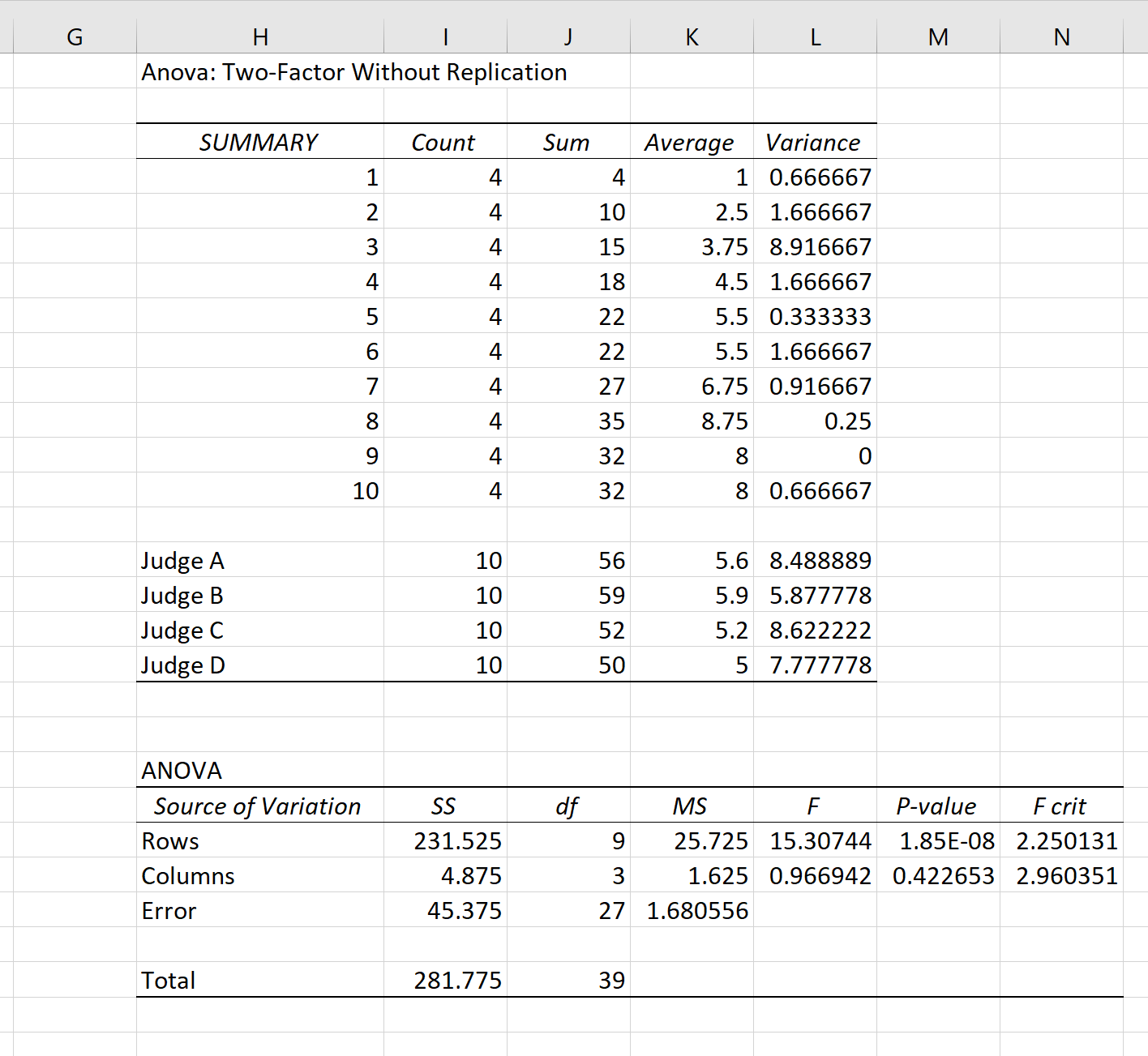
ผลลัพธ์ต่อไปนี้จะปรากฏขึ้น:

ขั้นตอนที่ 3: คำนวณค่าสัมประสิทธิ์สหสัมพันธ์ภายในคลาส

เราสามารถใช้สูตรต่อไปนี้เพื่อคำนวณ ICC ในกลุ่มผู้ประเมิน:

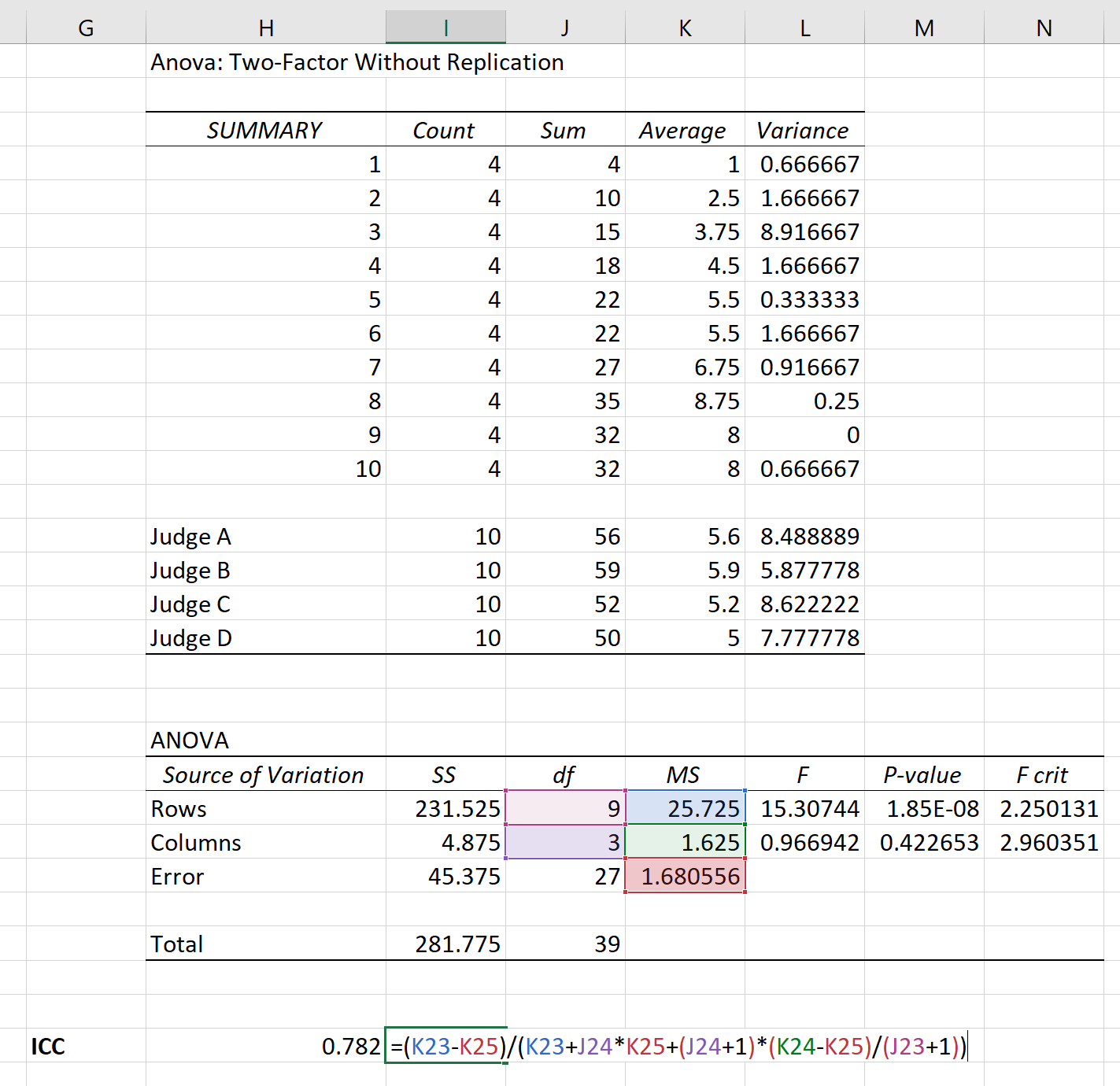
พบว่ามีค่าสัมประสิทธิ์สหสัมพันธ์ภายในคลาส (ICC) เท่ากับ 0.782

ต่อไปนี้เป็นวิธีการตีความค่าของสัมประสิทธิ์สหสัมพันธ์ภายในคลาสตาม Koo & Li :

• น้อยกว่า 0.50: ความน่าเชื่อถือต่ำ
• ระหว่าง 0.5 ถึง 0.75: ความน่าเชื่อถือปานกลาง
• ระหว่าง 0.75 ถึง 0.9: ความน่าเชื่อถือที่ดี
• มากกว่า 0.9: ความน่าเชื่อถือที่ดีเยี่ยม

ดังนั้น เราจะสรุปได้ว่า ICC ที่ 0.782 บ่งชี้ว่าผู้ประเมินต่างๆ สามารถทำคะแนนการสอบได้ด้วยความน่าเชื่อถือ “ดี”

หมายเหตุเกี่ยวกับการคำนวณ ICC

ICC มีหลายเวอร์ชันที่สามารถคำนวณได้ ขึ้นอยู่กับปัจจัยสามประการต่อไปนี้:

• รุ่น: เอฟเฟกต์สุ่มทางเดียว เอฟเฟกต์สุ่มสองทาง หรือเอฟเฟกต์ผสมสองทาง
• ประเภทของความสัมพันธ์: ความสม่ำเสมอหรือข้อตกลงสัมบูรณ์
• หน่วย: ผู้ประเมินรายเดียวหรือค่าเฉลี่ยของผู้ประเมิน

ในตัวอย่างก่อนหน้านี้ ICC ที่เราคำนวณใช้สมมติฐานต่อไปนี้:

• รุ่น: เอฟเฟกต์สุ่มสองทาง
• ประเภทของความสัมพันธ์: ข้อตกลงสัมบูรณ์
• หน่วย: ผู้ประเมินรายเดียว

สำหรับคำอธิบายโดยละเอียดเกี่ยวกับสมมติฐานเหล่านี้ โปรดดูที่ บทความนี้